Деление окружности на равные части можно выполнять при помощи угольников с углами 30, 60 и 45 градусов, транспортира или при помощи циркуля.
Приведём пример деления окружности на 3, 6 и 12 частей.
При делении на 3 части достаточно из любой точки окружности (например, точки А) провести дугу радиусом равным радиусу окружности – см. рисунок 29.
При делении на 6 частей дугу проводят 2 раза из противоположных точек окружности А и Б – см. рисунок 30.
Соответственно при делении окружности на 12 частей дугу проводят 4 раза из противоположных точек окружности.
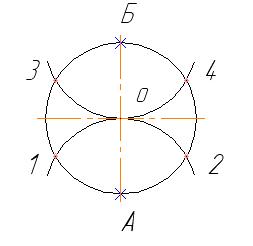
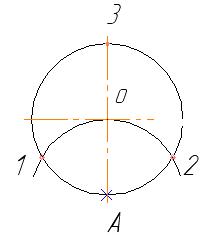
Рисунок 29 Рисунок 30
Сопряжения.
Сопряжения - это плавный переход от одной линии в другую по дуге окружности заданного радиуса.
Построить сопряжение это найти центр радиуса сопряжения и точки касания – точки плавного перехода из одной линии в другую.
Рассмотрим пример сопряжения двух сторон прямого угла.
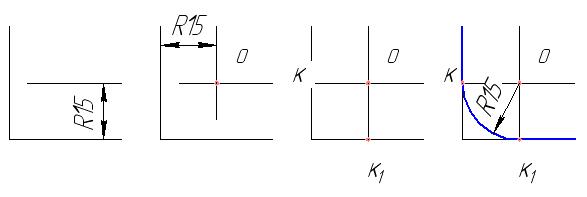
а) б) в) г)
Рисунок 31
Дано: расположение сторон прямого угла и значение радиуса сопряжения 15 мм.
Необходимо найти центр радиуса сопряжения – О и точки касания – К и К1 и построить сопряжение прямого угла.
Последовательность построения:
1. Параллельно одной стороне прямого угла проводим линию на расстоянии равной величине радиуса сопряжения – см. рисунок 31 а).
2. Аналогично проводится вторая линия параллельно второй стороне угла –см. рисунок 31 б). Пересечение двух засечек даёт нам центр радиуса сопряжения – точку О.
3. Для нахождения точек касания опускаем перпендикуляры из точки О на стороны прямого угла. Получаем точки К и К1 – см. рисунок 31 в).
4. Из точки О радиусом сопряжения, равным 15 мм проводим дугу сопряжения между точками касания К и К1 – см. рисунок 31 г).
Ниже представлены примеры:
-сопряжения прямой линии с дугой окружности – см. рисунок 32,
-сопряжение дуги с дугой - внутреннее – см. рисунок 33,
-сопряжение дуги с дугой – внешнее – см. рисунок 34,
-сопряжение дуги с дугой – смешанное – см. рисунок 35.
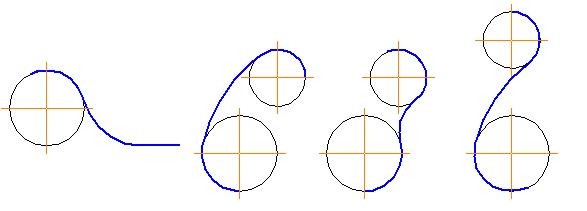
Рисунок 32 Рисунок 33 Рисунок 34 Рисунок 35
2.3 Лекальные и коробовые кривые.
Коробовые кривые состоят из сопрягающихся дуг окружностей различных диаметров. К таким кривым относят овал. овоид, завиток.
Лекальные кривые – кривые. заданные многими точками, представляющие ряд сопряжённых отрезков кривых, которые невозможно провести циркулем. Такие кривые строятся путём нахождения некоторого количества точек, которые предварительно соединяют от руки карандашом плавной тонкой линией, а затем обводят мягким карандашом по лекалу. Примером таких линий являются: синусоида, парабола, гипербола, спираль Архимеда и др.
Изучение и построение таких кривых предлагается студентам самостоятельно.
Уклоны и конусности.
Уклоном называется отношение катета АС к катету ВС треугольника АВС или тангенс угла АВС – см. рисунок 36
Перед размерным числом, определяющим уклон, наносится условный знак, острый угол которого должен быть направлен в сторону уклона. Уклоны выражаются в виде отношения или в процентах – см. рисунок 37
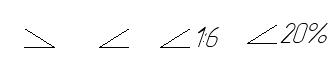
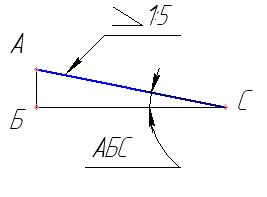
Рисунок 36 Рисунок 37
Конусностью называется отношение диаметра D окружности основания конуса к его высоте h. Если конус усечённый, то конусность определяется как отношение разности диаметров окружностей оснований конуса D и d к его высоте h –см. рисунок 38. Перед размерным числом, характеризующим конусность наносят условный знак в виде равнобедренного треугольника с вершиной, направленной в сторону вершины конуса. Конусность выражается в виде отношения или в процентах – см. рисунок 39.
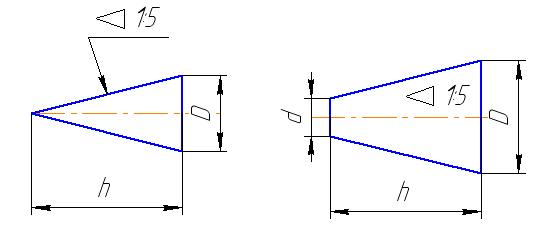
Рисунок 38

Рисунок 39






