В результате различного вида коротких замыканий в сложной энергосистеме возникает несимметричный режим. Расчет токов коротких замыканий в различных точках энергосистемы является важной инженерной задачей. Также расчеты выполняются методом симметричных составляющих.
В качестве примера рассмотрим определение тока однофазного короткого замыкания на землю в заданной точке простейшей энергосистемы. Символьная схема энергосистемы показана на рис. 110. Короткое замыкание фазы А на землю происходит в конце линии электропередачи.

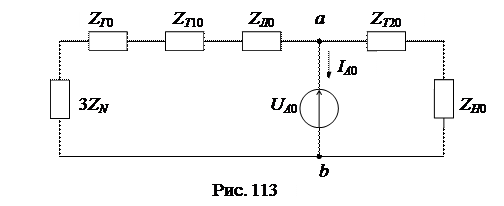
В соответствии с теоремой о компенсации заменим (мысленно) несимметричный участок в точке короткого замыкания несимметричным трехфазным генератором (U A, U B, U C, причем U A = 0). Несимметричную систему векторов напряжений разложим (мысленно) на симметричные составляющие U A 1, U A 2, U A 0. Для каждой из симметричных составляющих схема цепи совершенно симметрична и может быть представлена в однофазном виде. Поэтому составляются однофазные схемы для прямой (рис. 111), обратной (рис. 112) и нулевой (рис. 113) последовательностей.
 | |||
 |
Далее в соответствии с теоремой об эквивалентном генераторе производится свертка расчетных схем для каждой из симметричных составляющих относительно выводов несимметричного участка ab. В результате свертки получаются простейшие одноконтурные схемы (рис. 114а, б, в):
 |
Для каждой из расчетных схем (рис. 114а, б, в) составляются уравнения по 2-му закону Кирхгофа:

 (1)
(1)
 (2)
(2) 
 (3)
(3)
В полученной системе уравнений Кирхгофа содержится 6 неизвестных величин (I A 1, I A 2, I A 0, U A 1, U A 2, U A 0) и ее непосредственное решение невозможно. Поэтому система уравнений Кирхгофа дополняется тремя недостающими уравнениями, вытекающими из вида короткого замыкания. В рассматриваемом примере в точке короткого замыкания напряжение фазы А равно нулю (UA = 0), а также токи фаз В и С равны нулю (I B = I C = 0). Дополнительные уравнения будут иметь вид:

 (4)
(4)
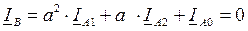 (5)
(5)
 (6)
(6)
В результате совместного решения системы из 6-и уравнений определяются симметричные составляющие токов I A 1, I A 2, I A 0. В рассматриваемом примере решение системы может быть выполнено в следующей последовательности.
1) Вычитаем почленно из уравнения (5) уравнение (6) и получаем:
 , откуда следует, что I A 1 = I A 2.
, откуда следует, что I A 1 = I A 2.
2) Складываем почленно уравнение (5) и уравнение (6) и с учетом, что а 2 – а = -1, получаем:  , откуда следует, что I A 1 = I A 2 = I A 0.
, откуда следует, что I A 1 = I A 2 = I A 0.
3) Складываем почленно уравнения (1), (2), (3) и с учетом уравнения (4) и равенства I A 1 = I A 2 = I A 0 получаем:
 , откуда следует решение для тока:
, откуда следует решение для тока:
 .
.
Все действительные токи определяются по методу наложения через соответствующие симметричные составляющие, например, ток короткого замыкания равен току фазы А:
 .
.






