С появлением ЭВМ и их широким применением для решения сложных математических задач были разработаны специальные топологические расчёта сложных электрических цепей, графов и матриц.
Схема сложной электрической цепи (рис. 83а) может быть заменена (представлена) направленным графом (рис. 83б) с соблюдением следующих условий:
1)узлы графа соответствуют узлам схемы;
2)ветви графа соответствуют ветвям схемы;
3) направление ветвей соответствует направлению токов в ветвях схемы.
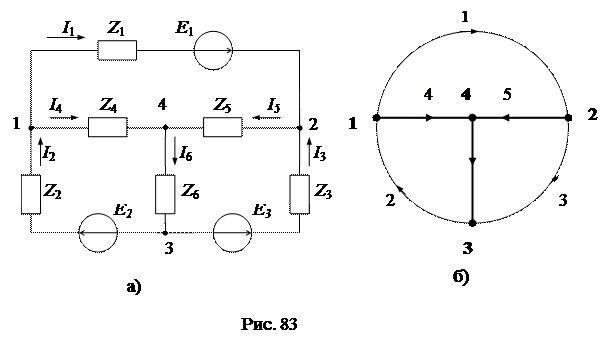 |
Любая часть графа называется подграфом. Минимальный связанный подграф, соединяющий все узлы графа и не образующий контуров, называется деревом графа (на схеме графа обозначается жирной линией). Для конкретного графа может быть составлено определенное множество вариантов деревьев, но в расчете схемы принимается любой из вариантов. Ветви графа, не входящие в его дерево, называются связями или хордами.
Структура графа и соответственно структура электрической схемы может быть описана с помощью топологических матриц или матриц соединения. Таких матриц несколько, для расчета электрических цепей используются две основные:  - матрица соединений «узлы-ветви» и
- матрица соединений «узлы-ветви» и 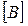 - матрица соединений «контуры-ветви».
- матрица соединений «контуры-ветви».
В общем случае сложная схема содержит «m» ветвей и «n» узлов, при этом максимальное число ветвей зависит от числа узлов:  .
.
Составим таблицу соединений «узлы-ветви» руководствуясь следующими правилами:
1 – ветвь выходит из узла,
-1 – ветвь входит в узел,
0 – отсутствие связи с узлом.
Т а б л и ц а 1
| № узла \ № ветви | ||||||
| -1 | ||||||
| -1 | -1 | |||||
| -1 | ||||||
| -1 | -1 |
Так как каждая ветвь имеет только один вход (-1) и один выход (+1), то сумма чисел по вертикали для любого столбца равна нулю. Из этого следует, что независимыми являются только 3 из 4 строк таблицы. Матрица соединений 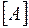 «узлы-ветви» (табл. 2) получается из приведенной выше таблицы путем вычеркивания любой строки (например, строки №4):
«узлы-ветви» (табл. 2) получается из приведенной выше таблицы путем вычеркивания любой строки (например, строки №4):
Т а б л и ц а 2
| № узла \ № ветви | ||||||
| -1 | ||||||
| -1 | -1 | |||||
| -1 |
Размерность матрицы соединений  «узлы-ветви» равна
«узлы-ветви» равна 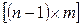 , где n -1 – число независимых узлов, m – число ветвей.
, где n -1 – число независимых узлов, m – число ветвей.
Независимыми называются контуры графа, образованные одной из хорд и ветвями дерева. Число независимых контуров соответствующих числу хорд графа: 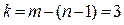 , контуры нумеруются по номеру хорды (1, 2, 3). Направление обхода контура принимается по направлению хорды, которая входит в состав этого контура.
, контуры нумеруются по номеру хорды (1, 2, 3). Направление обхода контура принимается по направлению хорды, которая входит в состав этого контура.
Составим таблицу соединений «контуры-ветви», руководствуясь следующими правилами:
1 – направление ветви совпадает с направлением обхода контура,
-1 – направление ветви не совпадает с направлением обхода контура,
0 - ветвь не входит в контур.
Т а б л и ц а 3
| № контура \ № ветви | ||||||
| -1 | ||||||
Данная таблица получила название матрицы соединений 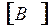 - «контуры-ветви».Размерность матрицы соединений
- «контуры-ветви».Размерность матрицы соединений  равна
равна  , где
, где  – число независимых контуров, m – число ветвей.
– число независимых контуров, m – число ветвей.
Если матрицы соединений 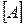 и
и 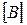 составлены верно, то должно выполняться условие:
составлены верно, то должно выполняться условие: 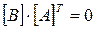 .
.






