Для больших наборов правил (тысяча и более) необходимо иметь математический («компьютерный») путь решения этих проблем. Для его изложения уточним и введем ряд дополнительных понятий и определений.
Предикат реализуется на конечном множестве U наборов входных аргументов. Множество U называют универсумом, любой из этих наборов – интерпретацией. Поскольку результатом действия предиката является 0 или 1, то интерпретации можно разделить на два класса: W, в котором предикат W истинен, и 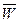 - где предикат W ложен.
- где предикат W ложен.
Замечание: вместо W часто используется название самого предиката. Пусть предикат имеет имя P. Множество истинности обозначается как P, а вместо 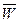 используем
используем  .
.
Предикат или его отрицание называют литералом.
В решении проблемы выводимости используются следующие понятия:
1. Если формула (3.52) справедлива на всех интерпретациях U, то она является общезначимой (тавтология)
2. Если формула (3.52) ложна на всех интерпретациях, то она невыполнима (противоречива).
3. Формула (3.52) необщезначима, если она не является общезначимой.
4. Формула (3.52) непротиворечива, если она не является противоречивой
Два предиката F и G эквивалентны (F º G), если они совпадают на множестве истинности (ложности). Для выводимости формула (3.51) должна быть общезначима.
В решении проблемы выводимости первоначально использовали формулу (3.52). Однако в прикладных математических операциях выяснилось, что проще доказать ложность отрицания цели.
В этом случае вместо выражения (3.52) используют выражение вида:
n _
Ç Ai Ç G. (3.53)
i = 1
Квантор выступает как одна из разновидностей предиката.
Заметим, что квантор общности не накладывает ограничений на свойства предикатов, в то время как квантор существования имеет серьезные ограничения по области действия: логическая зависимость справедлива только на подмножестве. В связи с этим с кванторами надо обращаться аккуратно. Например, справедливо выражение
("X)(F(X)ÇG(X)) = ("X)F(X)Ç("X)G(X). (3.54)
Если в (3.54) заменить конъюнкцию Ç на дизъюнкцию È, то справедливость теряется.
Аналогично справедливо
($X)(F(X)ÈG(X)) = ($X)F(X)È("X)G(X) (3.55)
При замене в (3.55) дизъюнкции È на конъюнкцию Ç справедливость теряется.
Для кванторов справедливы законы де Моргана:
 , (3.56)
, (3.56)
 .(3.57)
.(3.57)
Для того чтобы оперировать квантором существования, используют процедуру перехода от квантора существования к квантору общности. Это процедура называется сколемизацией.
Иллюстрируем ее на примере.
("x)($y) P(x, y),
x={1, 2}элементы множества x,
y={1, 2}элементы множества y,
отсюда множество интерпретаций U={1,1; 1,2; 2,1; 2,2}. Пусть предикат имеет значения P(1, 1) = 1; P(1, 2) = 0; P(2, 1) = 0, P(2, 2) = 1. Введем функцию

и получим
(" x)(" y)P(x, f (x)),
где f (x) – функция Сколема, в рамках которой квантор существования ведет себя как квантор общности. Очень часто квантор общности опускают при написании предикатов.
Заметим, что в предикатах используется предваренная (префиксная) нормальная форма: кванторы находятся слева от системы предикатов, которая называется матрицей.
Все дальнейшие теоретические выкладки проводятся для так называемой фразовой формы, представляющей собой конъюнктивную нормальную форму, где знаки конъюнкций связывают дизъюнкты. Такая форма носит название стандартной предикатной формы. Иногда в ней знаки конъюнкции опускаются и выписываются только дизъюнкты.
Переход от исходной предикатной формы к стандартной предикатной форме осуществляется поэтапно:
1) исключение импликаций по формуле эквивалентности;
2) замена отрицаний с помощью формул де Моргана;
3) замена квантора существования на квантор общности с использованием сколемизации;
4) перенесение дизъюнкций внутрь скобок дизъюнктов и приведение формулы к клаузальной (от clause - предложение) форме;
5) вынесение кванторов общности перед предикатами и их опусканием.
Перейдем к изложению решения проблем экспертных систем.
Проблема выводимости. Доказательство общезначимости (противоречивости) при решении проблемы выводимости в любом методе базируется на двоичном семантическом дереве (рис. 4.5). При построении дерева используются правила.
1. Каждая дуга/узел помечена литералом - предикатом или его отрицанием.
2. Из одного узла выходят две дуги, помеченные литералами.
3. Никакая ветвь не содержит двух противоположных литералов.

4. Никакая ветвь не содержит более одного вхождения одного литерала.
Если множество формул конечно, то соответствующее им семантическое дерево конечно. Каждому его узлу соответствует частичная интерпретация, сопоставляющая истинностные значения некоторым элементам.
Конечное семантическое дерево полно, если каждый его лист, т.е. конечная висячая вершина, соответствует некоторой всюду определенной интерпретации.
Формула является выполнимой, если, по крайней мере, для одного из листьев семантического дерева получено значение «истина». Следовательно, алгоритм выполнимости формул и выводимости результата является переборным и решает задачу для конечного семантического дерева.
Если в предикатах используются кванторы и функции, то семантическое дерево может быть бесконечным. Тогда требуется доказать: если некоторые свойства справедливы на части дерева, то они справедливы и на всем дереве.
Для решения проблемы выводимости сформулированы методы представления, из которых наибольшее распространение получил метод резолюции Робинсона (рис. 3.14).
Каждый дизъюнкт в этом методе называют фразой. Две фазы могут быть резольвированы друг с другом, обращаясь в пустой дизъюнкт, если одна из них содержит положительный n -местный литерал, а вторая негативный n -местный литерал того же предиката.
Абстрактная переменная резольвирует с любой конкретной переменной, принимая значения этой конкретной переменной.
Пусть имеется система правил (дизъюнктов)
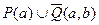 (3.58)
(3.58)
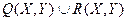 (3.59)
(3.59)
S(b) (3.60)
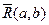 (3.61)
(3.61)

Необходимо определить, достижима ли цель P(a).
Возьмем отрицание цели
 . (3.62)
. (3.62)
Резольвируем (3.62) и (3.58) получаем
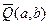 . (3.63)
. (3.63)
Резольвируем (3.63) и (3.59) получаем
R(a,b). (3.64)
Резольвируем (3.64) и (3.61) получаем
#. (3.65)
Иногда строят дерево резолюций, показанное на рис. 3.14.
Метод резолюций Робинсона позволяет работать и с функциями. Он решает проблему выводимости цели из данной системы правил.
При решении проблемы извлечения результата к системе правил добавляют дизъюнкт, состоящий из отрицания цели и цели.
Вместе с тем такой математический аппарат не всегда удобен для прикладных целей. В связи с этим в прикладных целях для поиска решений используют другие методы: поиск в глубину и в ширину – в языке ПРОЛОГ, прямая и обратная аргументация – в оболочке экспертной системы GURU.
Теперь возможно перейти к примеру конкретной прикладной ЭСРВ.
Для выполнения проектных работ необходимы специалисты в соответствии со штатным расписанием. Необходимо его «выполнить», т.е. осуществить прием на вакантные места. Отбор претендентов осуществляется по анкетным данным. Необходимо – в помощь руководителю – спроектировать соответствующую ЭСРВ (базу знаний).
Цель работы ЭСРВ – автоматизация интеллектуальных аспектов работы руководителя: выработка решений-советов и – после их согласования с руководством – принятие решений, передаваемых на объект управления системы/
Из-за относительной простоты проектируемой системы разработчиком является специалист-исследователь, совмещающий в себе функции эксперта, конечного пользователя (КП) и программиста. Ресурсные ограничения в данном случае не рассматриваются. Правила работы ЭСРВ формируются на основе представления исследователем-экспертом порядка работы КП по ручному управлению кадрами.
КП может быть несколько, поэтому система может иметь не одноуровневую (рис. 3.9), а двухуровневую структуру.
Первичные исследования процесса позволили сформировать структуру системы (рис. 3.15) и общее ее описание (рис. 3.16).
II. Концептуализация. В качестве терминов примем терминологию, использованную на рис. 3.15. Из рис. 3.15 видно, что в ЭСРВ отсутствует реальный объект управления, а, следовательно, система датчиков и табло.
Схема процесса управления в такой системе отображена на рис. 3.17.
База знаний представлена:
базой данных - таблицами Штатное расписание (А), Кадры (список наличного штатного персонала - Б), в том числе список претендентов В, принятых Г, скорректированный список принятых Д;
базой правил – таблицей правил.
Считается, что данные и правила достоверны и учет недостоверности результатов не проводится.
Предполагается, что в процессе работы КП с БЗ правила и результаты их работы могут корректироваться. Правила могут корректироваться и инженером по знаниям в процессе получения новых знаний о предметной области.
Работа ЭСРВ проводится в дискретном времени, состоящем по умолчанию из трех интервалов времени, составляющих сессию функционирования системы. Каждый интервал времени называют также циклом.
1) данными в виде таблиц А и Б;
2) системой продукций (правил) в виде таблицы правил;
3) математическим описанием дискретной (машина логического вывода) и непрерывной составляющей модели управляющей части;
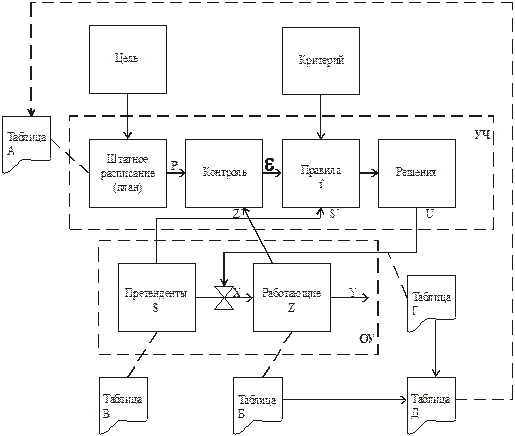
Рис. 3.15. Схема системы управления приемом на работу
После окончания сессии система должна вернуться в исходное состояние.
Формально описание ЭСРВ представлено:
4) описанием объекта управления в форме разностного уравнения;
5) описанием действия среды, проявляющемся в увольнении людей и появлении претендентов в начале каждого цикла.
Для описания позиций 3 – 5 введем дополнительные обозначения: (t) - дискретные моменты времени  [ t ] = [(t) - (t -1)] = const - интервал времени.
[ t ] = [(t) - (t -1)] = const - интервал времени.
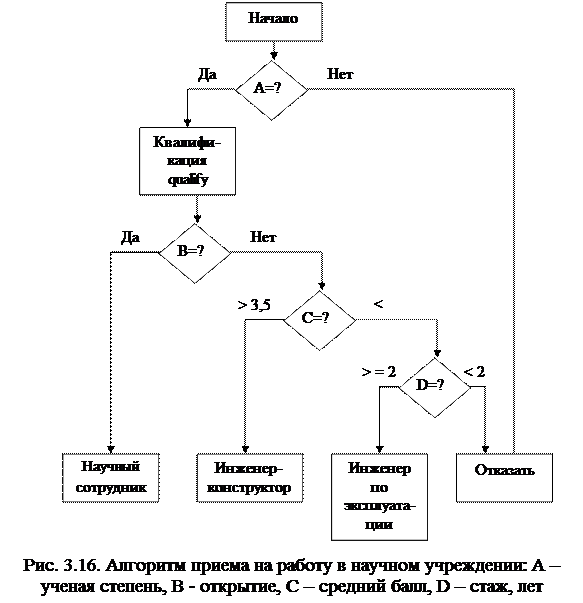 |
Таблица А.
Штатное расписание (начальное)
| Время | Должность | План | Факт | Вакансии |
| Научный сотрудник | ||||
| Инженер-конструктор | ||||
| Инженер по эксплуатации |
Считаем, что на интервале [ t ] скорости x, y, x', y', s, s' постоянны и меняются только на границе интервала времени.
Пусть [ t ] - один рабочий день.
Обозначим x [ t ], y [ t ] - число принятых и уволенных за день. Очевидно, что x, y, s – векторы. Например, x = { x 1, x 2, x 3}T, т - признак транспонирования, { xv, 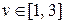 }, v =1 - научный сотрудник, v =2 - инженер-конструктор, v =3 - инженер по эксплуатации.
}, v =1 - научный сотрудник, v =2 - инженер-конструктор, v =3 - инженер по эксплуатации.
Значком (') на рис. 3.15 обозначена информация о соответствующих координатах: x= x', y=y', s = s'. План p может задаваться двояко: ежедневный; с накоплением (например, с начала месяца).
«Оцифруем» словесно выраженные решения r, суммарное количество которых R ( ) равно числу претендентов: i = 0 – «отказать», i = 1 – «научный сотрудник», i = 2 – «инженер-конструктор», i = 3 – «инженер по эксплуатации».
) равно числу претендентов: i = 0 – «отказать», i = 1 – «научный сотрудник», i = 2 – «инженер-конструктор», i = 3 – «инженер по эксплуатации».
 Тогда циклическая процедура представляет собой систему правил следующего вида
Тогда циклическая процедура представляет собой систему правил следующего вида
0, A = нет;
0, A = да, B = нет, C < 3.5, D < 2;
ir [ t ] = 1, A = да, B = да;
2, A = да, B = нет, C V 3.5;
3, A = да, B = нет, C < 3.5, D ³ 2. (3.66)
где 

Рис. 3.17. Процедура работы с
пользовательской БЗ: П - принимаемые;
В - вакансии.
Непрерывная составляющая управляющей части системы состоит из разностных уравнений:
wri [ t ] = wr – 1. i [ t ] + 1(ir [ t ]), если ir [ t ] ¹ 0, w0 i [0]=0, (3.67)
при решении u:
ui [ t ] = wri [ t ]. при r=R (3.68)
и
x[t]=u[t], u (t) _ e (t)(3.69)
e = p - z', (3.70)
где p – план приема по штатному расписанию, z’=z – информация о состоянии объекта управления (количестве работающих).
Описание объекта управления имеет вид разностного уравнения
z (t) = z (t -1) + [ t ](x [ t ] - y [ t ]). (3.71)
Таблица Б
Список штатного персонала (начальный)
| Время | Фамилия и о | Ученая степень | Открытия | Сред ний балл | Стаж | Статус | Должность |
| Водопьянов | Да | Да | 4,8 | работ | науч. сотр. | ||
| Каримов | Да | Да | 3,3 | работ | науч. сотр | ||
| Крамской | Да | Да | 4,2 | работ | науч. сотр | ||
| Крикунов | Да | Да | 3,5 | работ | науч. сотр | ||
| Трубецков | Да | Да | 4,1 | работ | науч. сотр | ||
| Крымов | Да | Нет | 4,0 | работ | инж.-конс | ||
| Мамедов | Да | Нет | 3,9 | работ | инж.-конс | ||
| Орлов | Да | Нет | 3,7 | работ | инж.-конс | ||
| Синцов | Да | Нет | 4,5 | работ | инж.-конс | ||
| Петрович | Да | Нет | 4,2 | работ | инж.-конс | ||
| Тараканов | Да | Нет | 4,1 | работ | инж.-конс | ||
| Травкин | Да | Нет | 5,0 | работ | инж.-конс | ||
| Хохлов | Да | Нет | 4,0 | работ | инж.-конс | ||
| Черкас | Да | Нет | 4,8 | работ | инж.-конс | ||
| Касымов | Да | Нет | 3,3 | работ | инж.-экспл | ||
| Контуров | Да | Нет | 3,0 | работ | инж.-экспл | ||
| Купцов | Да | Нет | 3,3 | работ | инж.-экспл | ||
| Ребров | Да | Нет | 3,4 | работ | инж.-экспл | ||
| Ремезов | Да | Нет | 3,4 | работ | инж.-экспл | ||
| Соколов | Да | Нет | 3,3 | работ | инж.-экспл | ||
| Тиунов | Да | Нет | 3,0 | работ | инж.-экспл | ||
| Троекуров | Да | Нет | 3,0 | работ | инж.-экспл | ||
| Время | Фамилия и о | Ученая степень | Открытия | Сред ний балл | Стаж | Статус | Должность |
| Щавель | Да | Нет | 3,2 | работ | инж.-экспл | ||
| Карпов | Да | Да | 3,2 | претен | |||
| Крылов | Да | Да | 3,1 | претен | |||
| Синцов | Да | Нет | 4,5 | претен | |||
| Симонов | Да | Нет | 3,9 | претен | |||
| Иванов | Да | Нет | 3,2 | претен | |||
| Козлов | Да | Нет | 3,4 | претен | |||
| Петров | Нет | Да | 4,0 | Претен | |||
| Гуров | Нет | Нет | 4,0 | Претен | |||
| Цветков | Да | Нет | 3,0 | претен |
Таблица правил
| Номер правила | Ученая степень | Открытия | Знак балл | Средний балл | Знак стаж | Стаж | Должность |
| Нет | отказать | ||||||
| Да | Да | науч. сотр. | |||||
| Да | Нет | ³ | 3,5 | инж.-конст. | |||
| Да | Нет | < | 3,5 | ³ | инж.-экспл | ||
| Да | Нет | < | 3,5 | < | отказать |
Наличие претендентов в цикле [ t ] характеризуется таблицей Кадры (статус «претенденты»). Уволенные определяются в режиме диалога в конце каждого цикла [t], кроме [ t ]=3 заменой статуса с «работающий» на «уволенный».
Заметим, что операции (3.70) и (3.71) удобно реализовать в рамках операций агрегирования базы данных. Процесс работы пользователя с реализованной на компьютере ЭСРВ представлен на рис. 3.17.






