Первая и вторая проблемы решается сочетанием аппарата описания знаний и аппарата логического вывода.
Для решения третьей проблемы используются различные методы, учитывающие неточность описания (фактор уверенности, нечеткие множества).
Из рис. 2.9 следует, что необходимо системно описать следующие блоки: база данных (БД), база правил (БП), машина логического вывода (МЛВ), блок объяснений, интерфейс пользователя (ИП).
Возможны два варианта описания:
1) использовать универсальный математический аппарат для всех блоков;
2) блоки описывать разными математическими методами, стыкующимися между собой.
В силу большого разнообразия природы блоков описание универсальным методом не представляется возможным.
Очевидно, что БП и блок объяснений должны описываться одним математическим аппаратом. Объяснения могут иметь различную форму: КАК получено решение (на основе какай системы правил), КАК звучит правило с определенным номером, в КАКИХ правилах используется тот или иной параметр, ПОЧЕМУ компьютер запрашивает данные для уточнения запроса.
Работа интерфейса предполагает введение запроса; получение ответа системы; получение объяснения и напоминает работу БД.
Таким образом, необходимы три вида математического описания: БД, БП, МЛВ.
К методам описания предъявляются следующие требования.
1. Однозначность описания.
2. Оперирование множествами и подмножествами.
3. Интеграция методов описания данных, описания знаний и методов логического вывода.
4. Простота получения решения.
5. Возможность описания непрерывных процессов.
6. Доходчивость, наглядность и простота понимания правил человеком.
В общем случае системная работа перечисленных блоков в части вывода результатов Y может быть описана в виде
Y = <X, P, B, R>, (3.49)
где X – множество базовых элементов (данных, называемых в теории экспертных систем и фактами); P – правила с условиями их применения; B – множество аксиом построения синтаксически правильных совокупностей; R – множество правил вывода. Результат Y в теории экспертных систем называют целью.
Совокупность <X, P> образует аппарат описания знаний в блоках БД и базе правил, совокупность <B, R> - закономерности вывода в блоке МЛВ.
Объяснение O в общем виде может быть описано
O = <Pi, i = 1, N>, (3.50)
где Pi - правила, участвовавшие при выводе данного результата. Они (рис. 3.11) запоминаются в процессе вывода (путь вывода помечен жирными линиями).
Для базы данных следует использовать реляционную алгебру, для базы правил и объяснений – методы описания знаний, для МЛВ – методы логического вывода.
Сочетание элементов X и P имеют свою специфику, поскольку базы данных имеют свою структуру.
Реляционная алгебра и методы описания знаний хорошо согласуются между собой.
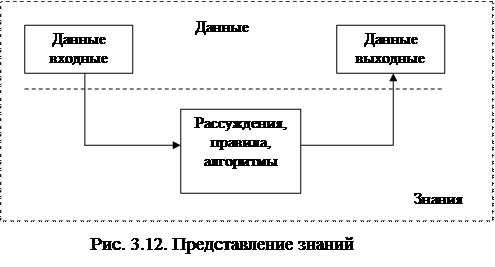
Знания – данные и связывающие их правила. Тогда связь данных и правил можно представить в виде рис. 3.12.
Одноуровневая система знаний может быть представлена в виде табл. 3.1, где A, B, C –имена данных; Ai, Bi, Ci, i = 1, 2 – значения данных.
При иерархической (многотабличной) системе правил некоторые цели могут стать ключами подчиненных таблиц.
Сложнее обстоит дело с сочетанием <X, P> и <B, R>, поскольку методы описания знаний и логического вывода первоначально развивались автономно.
 |
В связи с этим одной из задач экспертных систем является определение такого набора методов описания блоков, которые математически интегрировались бы в общую систему.
 |
Иными словами, требуется создание системной модели.
Таблица 3.1
Одноуровневая система правил
| Данные | Цель | ||
| A | B | C | G |
| A1 | B1 | C1 | G1 |
| A2 | B2 | C2 | G2 |
Такими интегрируемыми (системными) методами являются метод продукций (описание правил, знаний) и метод предикатов первого порядка (логический вывод результатов).
В методе продукций (правил) используется схема ЕСЛИ …, ТО…. Левую часть (условия) называют антецедентом, а правую – (результат) консеквентом. Описание достаточно наглядно, хорошо сочетается с методами логического вывода, в частности с предикатами первого порядка.
Продукции позволяют наглядно увидеть правила и обнаружить ошибки в их формировании.
Напомним, что описание знаний касалось блока базы правил. Перейдем к описанию процессов в МЛВ, т.е. к теории логического вывода.
Из методов логического вывода перечисленным ранее требования лучше всего удовлетворяет метод предикатов первого порядка.
Пусть имеется n исходных множеств X, что запишем как X n.
Если осуществляется преобразование: X n ® X, то говорят об алгебре.
Если осуществляется преобразование: X n ® {0, 1}, то говорят об отношениях.
Исчисление – совокупность правил оперирование с каким-либо символом (предикатами).
Предикат ( сказуемое) – отношение между множествами элементов, соответствующих аргументов. Например: Q (a 1, a 2, … an), где a n – аргументы, Q – предикат.
Предикат является предикатом первого порядка, если квантор не входит в сам предикат. Предикаты первого порядка «наследуют» кванторы от традиционной логики и строгую логику алгебры логики. Предикаты первого порядка охватывают большую часть отношений. Доказано, что в ряде частных случаев предикаты более высокого порядка могут быть сведены к предикатам первого порядка. Хотя предикаты первого порядка не позволяют описывать возможность и необходимость, убеждения, намерения, цели, метазнания (знания о знаниях), они охватывают широкий спектр возможностей и получили широкое распространение в построении ЭС.
Выделяют 3 вида аргументов предиката: абстрактные Q(X, Y) или отец (X, Y), конкретные Q(a, b) или отец (Иван, Петр), анонимные Q(_, b), где _ ставится в случае, когда конкретная величина аргумента не имеет значения.
Процедура перехода от абстрактных аргументов к конкретным называется – унификацией (аналог присвоения в алгоритмическом языке программирования).






