Розглянуті раніше, операції реляційної алгебри утворюють фундамент, на якому побудована більша частина сучасних мов запитів. Але конкретні мови, подібні SQL, пропонують додаткові операції, які широко використовуються у реальних додатках, а саме:
1. Оператор видалення кортежів-дублікатів δ (duplicate-elemination operetor) перетворює відношення - мультимножину у множину шляхом відкидання усіх копій кожного кортежу, за виключенням однієї.
2. Оператори агрегування (aggregations operators), призначені, наприклад, для знаходження підсумкових, середніх, максимальних і мінімальних значень у визначеному стовпці таблиці-відношення, строго кажучи, не відносяться до компетенції реляційної алгебри. Вони утворюють різновиди оператора групування.
3. В процесі групування (grouping) множина кортежів-рядків відношення розділяється на “групи ” у відповідності із вмістом одного або декількох компонентів. Потім до атрибутів –стовпців у середині кожної групи, як правило, застосовується певний оператор агрегування. Це дає можливість формувати самі різні запити, які неможливо створити у рамках традиційної реляційної алгебри.
Оператор групування γ (grouping operator) поєднує в собі можливості групування і агрегування.
4. Оператор сортування τ (sorting operator) перетворює відношення у список кортежів, упорядкованих у відповідності із деяким критерієм, який враховує вміст одного або декількох їх компонентів. Оператор τ слід застосовувати обережно, оскілки усі інші оператори реляційної алгебри здатні звертатися тільки до множин або мультимножин (але не до списків) кортежів. Тому оператор τ може використовуватися тільки на заключній стадії формування виразу, який складається із декількох ”вкладених ” операторів.
5. Оператор проекції π (projectionoperator) може бути наділений розширеними повноваженнями. Окрім звичайної проекції відношення на список атрибутів, оператор π у його загальній формі може виконувати додаткові функції над атрибутами-стовпцями відношення з метою створення нових атрибутів.
6. Оператор зовнішнього з’єднання (outerjoin operator) – це варіант оператора з’єднання, який дозволяє уникнути втрати “висячих ” (dangling) кортежів. Висячі кортежі включаються у результуюче відношення, і відповідні компоненти їх заповнюються значеннями null.
Видалення дублікатів.
Іноді виникає потреба у перетворенні відношення – мультимножини у множину. Для виконання подібних дій використовується оператор δ(R)
| А | В | А | В | |
Відношення R Відношення δ (R)
Оператори агрегування.
Існує ряд операторів, які застосовуються до множин або мультимножин атомарних значень однойменних компонентів кортежів з метою отримання деяких “агрегованих ”, тобто загальних, значень. До операторів агрегування відносяться наступні:
1. SUM – повертає суму значень у відповідному стовпці чисельного типу;
2. AVG – розраховує середнє арифметичне значення у відповідному стовпці чисельного типу;
3. MIN і MAX – розраховує, відповідно, мінімальне і максимальне значення у певному стовпці чисельного типу; якщо оператори застосовуються до стовпців рядкового типу, вони повертають, відповідно, перше і останнє значення із списку рядків, одсортованого у алфавітному порядку;
4. COUNT – повертає кількість значень у визначеному стовпці, або, що те ж саме, кількість кортежів у відношенні, уключаючи дублікати.
Приклад 5.7. Визначити для відношення наступні оператори агрегування SUM(B), AVG(A), MIN(A), MAX(B), COUNT(A).
| А | В |
1. SUM(B) = 2+4+2+2 = 10;
2. AVG(A) = (1+3+1+1+)/4 = 1,5;
3. MIN(A) = 1;
4. MAX(B) = 4;
5. COUNT(A) = 4.
Оператор групування.
Оператор групування γL(R) дозволяє групувати кортежі відношення R і застосовувати до атрибутів кортежів груп функції агрегування. Нижній індекс оператора γ задає список L елементів, кожний з яких може відноситися до любої із наступних категорій:
1. атрибути відношення R, до яких застосовується оператор γ; кожний подібний атрибут приймає участь у визначенні критерію групування R; у цьому випадку елемент називають групуючим атрибутом (grouping attribute);
2. оператори агрегування, які застосовуються до атрибутів відношення; ім’я результату агрегування задається після стрілки, що слідує за оператором агрегування; атрибут, виступаючий у ролі операнда функції агрегування, називають агрегованим атрибутом (aggregated attribute).
Результуюче відношення оператора γL(R) будується згідно наступного алгоритму:
1. Розбити множину кортежів відношення R на групи. Кожна група включає всі кортежі, що включають певні значення групованих атрибутів із списку L. Якщо груповані атрибути не задані, відношення R цілком розглядається як єдина група
2. Для кожної групи створити по одному кортежу, який складається із:
· значень атрибутів групування, що входять до відповідної групи;
· результатів агрегування, розрахованих стосовно агрегованих атрибутів для усіх кортежів групи, заданих у списку L.
Приклад 5.8.
Відношення StarsIn (title, year, starName) містить інформацію про акторів і про фільми за їх участю. Необхідно надати інформацію про акторів, що знялися не менш ніж у трьох фільмах, і привести рік випуску їх першого фільму.
Перший крок – це побудова груп кортежів з використанням атрибута starName у якості атрибута групування. Потім – це розрахунок для кожної групи значень операторів агрегування MIN (year) і COUNT (title). Створимо вираз групування
γstarName, MIN (year)→minYear, COUNT (title)→ctTitle (StarsIn),
де: γ – оператор групування; starName –атрибут групування; MIN (year)→minYear – агрегований атрибут year, до якого застосовується оператор агрегування MIN, і який отримує нову назву minYear; COUNT (title)→ctTitle – агрегований атрибут title, до якого застосовується оператор агрегування COUNT, і який отримує нову назву ctTitle; StarsIn – вихідне відношення.
Повний алгоритм виконання запиту для Прикладу 5.8 відображено у вигляді дерева виразів на рис.5.11.

Рис.5.11. Дерево виразів, яке представляє SQL –запит із Прикладу 5.8.
Оператор розширеної проекції.
Позначається як πL(R). Список L може містити елементи наступних типів:
1. окремий атрибут відношення R;
2. вираз виду x → y, де x, y – найменування атрибутів; елемент x → y списку L передбачає перейменування атрибута x відношення R в y;
3. вираз виду E → z, де E – вираз, який може включати найменування атрибутів, константи, арифметичні і строкові оператори, z – нове ім’я атрибута, яке є результатом розрахунку виразу E.
У процесі розрахунку оператора розширеної проекції кожний кортеж відношення розглядається окремо. Таким чином, кількість кортежів відношення-результату співпадає із вихідним відношенням R і може містити кортежі-дублікати.
Приклад 5.9.
Визначити результат розширеної проекції πA, B+C→X(R). Представлено на рис.5.12.
| A | B | C | A | X | |
Відношення R πA, B+C→X(R)
Рис.5.12. Розширена проекція відношення R
Оператор сортування.
Оператор сортування позначається як τL(R). Результатом розрахунку виразу τL(R), де R – деяке відношення, а L – список певних атрибутів R, являється те ж саме відношення R, але його кортежі переставлені у тому порядку, який задано на основі списку L. Якщо L представляє собою список атрибутів A1, A2, …,An, кортежі спочатку упорядковуються по значенням компонентів A1. Потім кортежі, що мають однакові значення A1, упорядковуються по значенням компоненти A2. Аналогічні процедури сортування відбуваються стосовно інших атрибутів списку L. Оскільки оператор сортування впливає на порядок слідування кортежів, застосування оператора слід бути максимально “зовнішнім ” стосовно інших операторів алгоритму обробки запиту.
Оператори зовнішнього з’єднання.
Оператори зовнішнього з’єднання – це спеціальні різновиди оператора з’єднання, які дозволяють уключати у його результуюче відношення деякі “висячі ” (dangling) кортежі, які не співпадають у атрибутах, загальних для двох відношень, ні з одним кортежем другого відношення. Оператори зовнішнього з’єднання підтримуються у більшості комерційних СУБД. Існують три різновиди операторів зовнішнього з’єднання:
· Оператор зовнішнього з’єднання; позначається як R  º
º 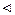 S. Результат операції зовнішнього з’єднання формується із відношення R
S. Результат операції зовнішнього з’єднання формується із відношення R 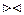 S, з наступним включенням усіх висячих кортежів відношень R і S. У результуючому відношенні компонентам висячих кортежів R для атрибутів, відсутніх в R, і компонентам висячих кортежів S для атрибутів, відсутніх в S, присвоюється спеціальне значення null, або вони позначаються символом ^.
S, з наступним включенням усіх висячих кортежів відношень R і S. У результуючому відношенні компонентам висячих кортежів R для атрибутів, відсутніх в R, і компонентам висячих кортежів S для атрибутів, відсутніх в S, присвоюється спеціальне значення null, або вони позначаються символом ^.
· Оператор лівого зовнішнього з’єднання, позначається як R  º
º 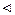 L S. Результат операції зовнішнього з’єднання формується із відношення R
L S. Результат операції зовнішнього з’єднання формується із відношення R 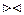 S, з наступним включенням усіх висячих кортежів відношень R. У результуючому відношенні компонентам висячих кортежів R для атрибутів, відсутніх в R, присвоюється спеціальне значення null, або вони позначаються символом ^.
S, з наступним включенням усіх висячих кортежів відношень R. У результуючому відношенні компонентам висячих кортежів R для атрибутів, відсутніх в R, присвоюється спеціальне значення null, або вони позначаються символом ^.
· Оператор правого зовнішнього з’єднання R  º
º 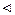 R S. Результат операції зовнішнього з’єднання формується із відношення R
R S. Результат операції зовнішнього з’єднання формується із відношення R 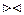 S, з наступним включенням усіх висячих кортежів відношень S. У результуючому відношенні компонентам висячих кортежів S для атрибутів, відсутніх в S, присвоюється спеціальне значення null, або вони позначаються символом ^.
S, з наступним включенням усіх висячих кортежів відношень S. У результуючому відношенні компонентам висячих кортежів S для атрибутів, відсутніх в S, присвоюється спеціальне значення null, або вони позначаються символом ^.
Приклад 5.10. Якщо U і V представляють екземпляри відношень, показані на рис.5.13, тоді в результаті виконання операцій R  º
º 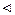 S, R
S, R  º
º 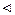 L S. і R
L S. і R  º
º 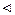 R S будемо мати відношення, що показані на цьому ж рис.5.13.
R S будемо мати відношення, що показані на цьому ж рис.5.13.

| A | B | C | B | C | D | |
Відношення U Відношення V
| A | B | C | D |
| ^ | |||
| ^ | |||
| ^ |
Відношення U  º
º 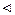 V
V
| A | B | C | D |
| ^ | |||
| ^ |
Відношення U  º
º 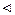 L V.
L V.
| A | B | C | D |
| ^ |
Відношення U  º
º 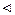 R V
R V
Рис.5.13 Операції зовнішнього з’єднання відношень U і V






