Определение. Многочленом (полиномом) называется выражение вида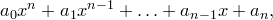 
где 
— элементы некоторого поля 
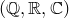, x — буква, 
– коэффициенты полинома, a0 – старший коэффициент.
Степенью многочлена называется максимальная из степеней его одночленов, тождественный нуль не имеет степени(a0!= 0).
Сложение многочленов
Если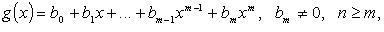 
то
где
Умножение многочленов
где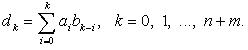 
В частности 
Деление многочленов с остатком. Существование и единственность частного и остатка.
Алгоритм деления с остатком
Для любых f(x), g(x) существуют q(x) (частное) и r(x) (остаток), такие, что f(x)=g(x)q(x)+r(x), причем степень r(x) < степени g(x) или r(x) = 0. Многочлены g(x) и r(x) определены однозначно.
Частное и остаток находят с помощью так называемого правила деления "уголком".
Пример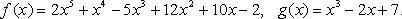 
Значение многочлена. Корень многочлена. Теорема Безу и ее важнейшее следствие.
Теорема Безу утверждает, что остаток от деления многочлена P(x) на двучлен x − a равен P(a).
Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).
Доказательство
Поделим с остатком многочлен P(x) на многочлен x − a:
P(x) = (x − a)Q(x) + R(x).
Так как deg R(x) < deg(x − a) = 1, то R(x) — многочлен степени не выше 0. Подставляя x = a, поскольку (a − a)Q(a) = 0, имеем P(a) = R(a).
Следствия
- Число a является корнем многочлена p(x) тогда и только тогда, когда p(x) делится без остатка на двучлен x − a (отсюда, в частности, следует, что множество корней многочлена P(x) тождественно множеству корней соответствующего уравнения P(x) = 0).
- Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
- Пусть α — целый корень приведённого многочлена A(x) с целыми коэффициентами. Тогда для любого целого k число A(k) делится на α-k.
Схема Горнера(вывод формул)
Если 
то при делении f(x) на g(x) частное q(x) имеет вид
где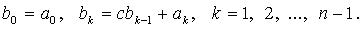 
Остаток r находится по формуле 
Рациональные корни многочленов с целыми коэффициентами.
Теорема о рациональных корнях многочлена
Если многочлен 
с целыми коэффициентами имеет рациональный корень x0=p/q, то число p является делителем числа a0 (свободного члена), а число q является делителем числа An (старшего коэффициента).
Доказательство.
Замечание. Эта теорема фактически позволяет находить корни многочленов высших степеней в том случае, когда коэффициенты этих многочленов − целые числа, а корень − рациональное число.
Теорему можно переформулировать так: если нам известно, что коэффициенты многочлена − целые числа, а корни его − рациональны, то эти рациональные корни могут быть только вида x0=p/q где p является делителем числа a0 (свободного члена), а число q является делителем числа An (старшего коэффициента).
Пусть все коэффициенты многочлена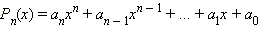 
являются целыми числами, и пусть целое число a является корнем этого многочлена.
Так как в этом случае 
то отсюда следует, что коэффициент A0 делится на a.
