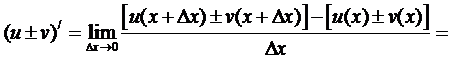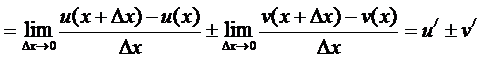Определение предела функции в точке. Предел суммы, произведения, частного двух функций.
Функция F(x) имеет предел A в точке X0, предельной для области определения функции F(x), если для каждой окрестности предела A существует проколотая окрестность точки X0, образ которой при отображении F(x) является подмножеством заданной окрестности точки A.
Предел суммы, разности, произведения и частного двух последовательностей
Если две последовательности {xn} и {yn} имеют пределы, равные соответственно a и b, то:
а) Последовательность {xn±yn} имеет предел равный a ±b, т. е.
lim[n―∞](Xn±Yn)=lim[n―∞]Xn±lim[n―∞]Yn=a±b
Это свойство распространяется на случай любого фиксированнго числа слагаемых.
б) Последовательность {xn yn} имеет предел равный ab, т. е.
lim[n―∞](Xn*Yn)=lim[n―∞]Xn*lim[n―∞]Yn=a*b
Это свойство распространяется также на случай любого фиксированного числа сомножителей.
lim[n―∞]KXn=K lim[n―∞]Xn
Постоянный множитель можно выносить за знак предела при любом постоянном k.
с) Последовательность {Xn/Yn} имеет предел равный a/b, т. е.
lim[n―∞](Xn/Yn)=lim[n―∞]Xn/lim[n―∞]Yn=a/b
при условии, что все Yn не равны нулю и limYn=b!=0.
Без доказательства суммы Доделаю позже
Определение производной, ее геометрический и физический смысл.
Пусть в некоторой окрестности точки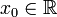 
определена функция 
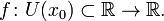Производной функции называется такое число, что функцию в окрестности U(x0) можно представить в виде
f(x0 + h) = f(x0) + Ah + o(h)
если A существует.
Геометрический и физический смысл производной
Тангенс угла наклона касательной прямой
Если функция 
имеет конечную производную в точке x0, то в окрестности U(x0) её можно
приблизить линейной функцией
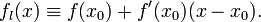
Функция fL называется касательной к f в точке x0. Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.
Скорость изменения функции
Пусть s = s(t) — закон прямолинейного движения. Тогда v(t0) = s'(t0) выражает мгновенную скорость движения в момент времени t0. Вторая производная a(t0) = s''(t0) выражает мгновенное ускорение в момент времени t0.
Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x).
Примеры
Пусть f(x) = x2. Тогда
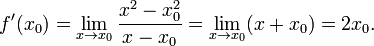
Пусть f(x) = | x |. Тогда если то
f'(x0) = sgn x0,
где sgn обозначает функцию знака. Если x0 = 0, то а следовательно f'(x0) не существует.
Теорема о непрерывности дифференцируемой функции
Непрерывность дифференцируемой функции
Теорема 1. Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция f непрерывна на (a, b).
Доказательство
Возьмем произвольное фиксированное число x (a,b).
По условию теоремы
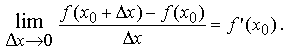
Следовательно, в малой окрестности числа x0 можно определить функцию α = α(Δx), стремящуюся к нулю при dX->0 такую, что
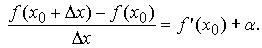
Но тогда и, следовательно, функция f непрерывна при x = x0. Так как число x0 – произвольное, то функция f непрерывна на всем интервале (a, b).
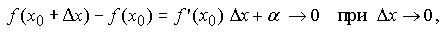
Теорема доказана.
Из доказанной теоремы непосредственно вытекает, что в точках разрыва функция не может быть дифференцируемой.
Однако из непрерывности функции на интервале (a, b) не следует дифферецируемость функции в каждой точке интервала (a, b). Например, функция непрерывна на всей числовой прямой, но эта функция недифференцируема при x = 0. В самом деле, предел (1) не зависит от знака приращения аргумента Δx. Для функции же имеем, если x = 0 придать приращение Δx > 0, то Δy = Δx, а если Δx < 0, то Δy = − Δx. Таким образом 
Следовательно, функция недифференцируема при x = 0.
Производная суммы, произведения, частного двух функций.
1) (u±v)’=u’±v’,
2) (u·v)’=u’v+v’u,
3) (v/u)'=(u’v-uv’)/u^2
