Семестр
На очном отделении:
Лекция № 1. Алгебраическая форма комплексного числа. Действия над комплексными числами, записанными в алгебраической форме.
Лекция № 2. Тригонометрическая форма комплексного числа. Действия над комплексными числами, записанными в тригонометрической форме.
Лекция № 3. Извлечение корня n-й степени из комплексного числа.
Лекция № 4. Перестановки. Инверсии. Транспозиции. Теорема о транспозиции в перестановке.
Лекция № 5. Определители порядка n. Свойства определителей.
Лекция № 6. Миноры. Алгебраические дополнения. Разложение определителя по строке (столбцу).
Лекция № 7. Элементарные преобразования систем линейных уравнений. Равносильные системы.
Лекция № 8. Решение систем линейных уравнений методом Гаусса.
Лекция № 9. Решение систем линейных уравнений методом Крамера.
На заочном отделении:
Лекция № 1. Комплексные числа.
Лекция № 2. Определители.
Семестр
На очном отделении:
Лекция № 1. Операции над матрицами. Свойства этих операций.
Лекция № 2. Обратная матрица. Критерий существования обратной матрицы.
Лекция № 3. Векторные пространства. Свойства векторных пространств.
Лекция № 4. Линейно зависимые и линейно независимые системы векторов.
Лекции № 5,6. Максимальные линейно независимые подсистемы системы. Основная теорема о линейной независимости.
Лекция № 7. Базис векторного пространства. Координаты вектора в базисе.
Лекция № 8. Эквивалентные системы векторов. Линейная оболочка системы векторов.
Лекция № 9. Ранг матрицы. Теорема о ранге матрицы.
Лекция № 10. Критерий совместности системы линейных уравнений.
Лекции № 11, 12. Однородные системы линейных уравнений. Фундаментальная система решений однородной системы.
Лекция № 13. Алгебраические операции. Свойства.
Лекция № 14. Группы. Свойства групп.
Лекция № 15. Подгруппы. Признаки подгруппы.
Лекция № 16. Кольца. Свойства колец. Подкольца.
Лекция № 17. Поля. Свойства полей. Подполя.
На заочном отделении:
Лекция № 1.Матрицы и действия с ними.
Лекция № 2. Линейные векторные пространства.
Лекция № 3. Ранг матрицы.
Лекция № 4. Однородные системы линейных уравнений.
Лекции № 5. Группы. Кольца. Поля.
Семестр
На очном отделении:
Лекция № 1. построение кольца многочленов от одной переменной.
Лекция № 2. Отношение делимости. НОД многочленов.
Лекция № 3. Взаимно простые многочлены.
Лекция № 4. Корни многочлена. Кратные корни. Схема Горнера.
Лекция № 5. Основная теорема алгебры многочленов. Следствия. Формулы Виета.
Лекция № 6. Решение уравнений 3-й степени.
Лекция № 7. Приводимые и неприводимые многочлены. Свойства.
Лекция № 8. Разложение многочлена на неприводимые множители. Неприводимость многочлена над полями  и
и 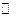 .
.
Лекция № 9. Неприводимость многочлена над полем  . Критерий Эйзенштейна.
. Критерий Эйзенштейна.
На заочном отделении (6 семестр):
Лекция № 1. Отношения делимости в кольце многочленов от одной переменной.
Лекция № 2. Основная теорема алгебры многочленов.
Лекция № 3. Рациональные корни многочленов с рациональными коэффициентами.
Лекция № 4. Приводимые и неприводимые многочлены.
Семестр
На очном отделении:
Лекция № 1. Векторные пространства. Базис и размерность пространства. Подпространство.
Лекции № 2,3 Пересечение и сумма подпространств. Прямая сумма подпространств. теорема о размерности суммы подпространств.
Лекция № 4. Изоморфизм векторных пространств.
Лекция № 5,6. Произведение числовой матрицы на векторную матрицу-столбец. Свойства этого произведения. Матрица перехода от одного базиса к другому.
Лекция № 7. Линейные операторы векторного пространства. Ядро и образ линейного оператора. Матрица линейного оператора.
Лекция № 8. Связь между матрицами одного и этого же линейного оператора в разных базисах.
Лекция № 9. Характеристический многочлен и характеристические корни матрицы линейного оператора.
Лекция № 10. Собственные векторы и собственные значения линейного оператора.
Лекция № 11. Линейные операторы с простым спектром. Приведение матрицы к диагональному виду.
Лекция № 12. Группы. Свойства групп. Подгруппы.
Лекция № 13. Циклические группы.
Лекция № 14. Классификация циклических групп.
Лекция № 15. Смежные классы по подгруппе. Свойства. Теорема Лагранжа.
Лекция № 16. Нормальные делители. Фактор-группы.
Лекция № 17. Теоремы о гомоморфизмах.
На заочном отделении (7 семестр):
Лекция № 1. Векторные пространства. Изоморфизм векторных пространств.
Лекция № 2. Преобразования координат.
Лекция № 3.Линейные операторы.
Лекция № 4. Группа. Циклические группы.




