Рассматриваемый в этом разделе метод применяется при проектировании сложных автоматических систем, включающих нелинейные элементы, а также звенья, параметры которых изменяются в процессе функционирования. Другими словами, задача синтеза регуляторов может рассматриваться в классе нелинейных нестационарных систем, поведение которых описывается дифференциальными уравнениями высокого порядка. Степень эффективности метода в основном определяется возможностями используемой ЭВМ, поскольку его базовое положение — численные методы решения дифференциальных и интегральных уравнений.
Что касается методов решения дифференциальных уравнений, то для них построены не только вычислительные схемы, но исследованы такие важные для практики вопросы, как сходимость и устойчивость, оценка погрешности, реализация алгоритмов на ЭВМ.
Численные методы решения ДУ (методы Эйлера, Рунге–Кутта и др.) являются основным инструментом исследования и анализа САУ: они являются универсальными и эффективными, так как позволяют находить приближенное решение для широкого класса, как систем, так и задач расчета и проектирования.
Однако численные методы имеют и недостатки: они не позволяют непосредственно, как аналитические методы, вскрыть причины того или иного поведения системы, поскольку они позволяют лишь получить конкретный результат (числовые значения) для конкретных исходных данных.
При решении же таких задач, как синтез регуляторов численные методы в инженерном содержании оказываются весьма эффективными, поскольку позволяют построить не только алгоритмы решения задач (иногда достаточно сложные), но и охватить широкий класс систем, включая нелинейные и нестационарные.
Изложим основное содержание метода синтеза регуляторов. Первый этап на пути построения численного метода решения задачи Коши состоит в замене отрезка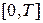 
— области непрерывного изменения аргумента множеством, которое представляет собой конечное число точек 
и называется сеткой. Сами точки 
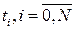называются узлами сетки с шагом 
Будем рассматривать, как правило, равномерную сетку, когда 
и 
Функции, которые определены лишь в узлах сетки, называются сеточными
Численные методы решения дифференциальных уравнений позволяют найти решение дифференциального уравнения вида
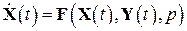(3.12)
где
— вектор-функция входа;
— вектор-функция выхода;
— вектор параметров системы.
Например, используя метод Эйлера, реализуемый по следующей вычислительной схеме
,
можно, полагая, что и 
известны, легко рассчитать функции 
Таким образом, задача анализа имеет решение в виде сеточных функций (рис. 3.4).
Рис. 3.4. К иллюстрации постановок задач анализа и синтеза регуляторов методом Эйлера
В полученном численным образом решении дифференциального уравнения в неявном виде учтены конкретные, текущие значения параметров регулятора .
Задача синтеза регулятора. Положим, что найдена система ДУ скалярной автоматической системы, представленное в форме Коши. Считаем, что регулятор включен последовательно и (или) параллельно. Численные значения параметров регулятора 
подлежат расчету (остальные параметры САУ известны).
Выполняя интегрирование дифференциального уравнения, описывающего динамику системы управления получить дискретные значения выходного сигнала. Дискретные значения зависят не только от 
, но в неявной форме и от параметров регулятора, т.е. 
(рис. 3.4).
Оптимальные значения параметров находятся минимизацией, например, функционала вида
Если же, например, система (3.54) описывает линейную многомерную стационарную САУ, т.е.
(3.13)
то численные значения параметров регулятора находятся путем минимизации функционала вида
где 
и 
— соответственно реальные и эталонные выходные сигналы системы.
