Рассмотрим линейную алгебраическую систему, записанную в виде векторно-матричного уравнения
, (4.5)
где 
– невырожденная 
матрица коэффициентов данной системы; 
– ненулевой 
-мерный вектор свободных членов; 
– -мерный вектор неизвестных (решение, если трактовать (4.5) как верное равенство).
Пусть правая часть (4.5) получила приращение («возмущение») 
, т.е. вместо истинного вектора используется приближенный вектор 
. Реакцией решения на возмущение правой части будет вектор поправок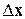 
, т.е. если – решение (4.5), то 
– решение уравнения
(4.6)
Нормы векторов.
– октоэдрическая 
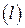норма
– сферическая (Евклидова) норма
– кубическая (С) норма
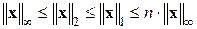
Норма матрицы связана с нормой вектора зависимостью
,
,
,
– спектральная норма, где 
– число сингулярности, 
,
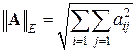
Подставляя (4.5) и (4.6) получаем
из которого находим ее явное выражение
(4.7)
Нормируя равенства (4.5) и (4.7) имеем
и 
,
где матричная норма должна быть согласованной с выбранной векторной нормой. Эти два числовых неравенства одинакового смысла можно перемножить:
.
Из последнего делением на 
получаем связь между относительными погрешностями результата и исходных данных
(4.8)
Положительное число 
– коэффициент этой связи – называют числом (мерой) обусловленности матрицы и обозначают 
(от английского слова conditioned – «обусловленный»)[2].
Легко показать, что то же самое число служит коэффициентом роста относительных погрешностей при неточном задании элементов матрицы в (4.5). А именно, если матрица получила возмущение 
и – решение возмущенной системы
,
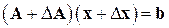то справедливы равенства
и 
(4.9)
Теорема 4.1. Пусть – данное, а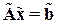 
– возмущенное линейные операторные уравнения с относительными уровнями возмущений 
и 
. Тогда, если 
, то эти уравнения одновременно однозначно разрешимы и справедлива оценка относительной погрешности решения, имеющая вид
.
Итак, неравенства (4.8) и (4.9) показывают, что чем больше число обусловленности, тем сильнее сказывается на решении линейной системы ошибка в исходных данных.
Если число велико, то система считается плохо обусловленной. Говорить о том, «что такое хорошо и что такое плохо», в отрыве от контекста решаемой задачи почти бессмысленно, так как здесь может играть роль размерность задачи, точность, с которой должно быть найдено ее решение, точность представления чисел в ЭВМ и т.п. Однако можно дать оценку снизу числа обусловленности. А именно, если используются подчиненные матричные нормы (для которых норма единичной матрицы есть единица), то, очевидно,
,
т.е. число обусловленности не может быть меньше 1. Можно также указать верхнюю границу для чисел обусловленности, превышение которой при решении линейных систем на конкретной ЭВМ может привести к заведомо ложным результатам. Так, решение считается надежным, если 
(здесь macheps – машинная eps) или даже 
. При этом заметим, что масштабированием матрицы путем умножения на скаляр 
ее обусловленность не улучшить, ибо
.
Очевидно, число обусловленности зависит от выбора матричной нормы (индуцированной, как правило, той или иной векторной нормой, в терминах которой характеризуется относительная погрешность решения алгебраической системы). Однако нетрудно получить оценку числа обусловленности через собственные числа матрицы. Действительно, пусть собственные числа 
матрицы упорядочены по модулю:
,
т.е. спектральный радиус матрицы есть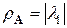 
. Тогда в силу известного неравенства 
и соотношения между собственными числами прямой и обратной матриц, имеем
.
Таким образом, оценкой снизу меры обусловленности матрицы может служить величина 
(называемая иногда числом обусловленности Тодда или Тодта). Для симметричных матриц эта оценка и на самом деле является числом обусловленности, соответствующим спектральной норме матрицы (индуцированной спектральной нормой вектора). Учитывая смысл собственных чисел матрицы, можно сказать, что число обусловленности показывает величину отношения наибольшего коэффициента растяжения вектора посредством линейного преобразования к наименьшему.
Следует отметить, что непосредственный подсчет чисел обусловленности, особенно при большой размерности матриц, является весьма дорогостоящим делом из-за необходимости обращать матрицы или находить их собственные значения. Поэтому зачастую о приемлемости порядка возможного роста относительной погрешности результата решения какой-либо алгебраической задачи относительно данной матрицы судят либо по каким-то достаточным признакам (например, по доминированию элементов главной диагонали матрицы), либо на основе теоретического изучения матрицы, либо путем применения специальных алгоритмов приближенного оценивания . Исследование матриц на обусловленность может быть естественным образом связано со способом решения той или иной алгебраической задачи относительно данной матрицы.
