Если известны изображения входа 
и передаточная функция 
то по формуле (1.5) можно найти изображение выхода, а путем обратного преобразования — и сам выходной процесс.
Таким образом, передаточная функция в целом характеризует динамические свойства системы (при нулевых начальных условиях).
Введем понятие дельта - функции 
Дельта - функцией называется функция, которая обладает следующими свойствами:
(1.10)
Иногда 
вводят как производную от единичной функции 
т.е.
(1.11)
Дельта-функция имеет производные любого порядка. Поскольку 
то, учитывая (1.11), имеем 
т.е. изображением является единица.
Теперь найдем изображение выхода, если входом является — дельта-функция.
Реакцию САУ на единичное импульсное воздействие, т.е. на 
на входе при нулевых начальных условиях называют импульсной переходной или весовой функцией (ИПФ) системы 
Найдем изображение ИПФ:
(1.12)
Отсюда следует важный факт: передаточная функция равна изображению по Лапласу от ИПФ и соответственно
(1.13)
ИПФ, как и передаточная функция, является исчерпывающей характеристикой САУ при нулевых начальных условиях. ИПФ имеет вид, представленный на рис. 1.3.
Рис. 1.3. ИПФ системы
Найдем соотношение, связывающее входной сигнал 
выходной процесс 
и ИПФ. Имеем
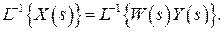(1.14)
Зависимость (1.14) представляет собой изображение вынужденного сигнала системы; формула для вынужденного процесса во временной области имеет вид
(1.15)
Эта формула, как и зависимость (1.14), справедлива при нулевых начальных условиях. ИПФ может быть построена как обратное преобразование Лапласа от ПФ 
По виду ИПФ можно определить время регулирование системы управления и другие ее характеристики. Но более важной ее особенностью является то, что с ее помощью можно, используя зависимость (1.15) определить выходной сигнал системы во временной области, используя вид входного сигнала, представленного также во временной области.
Более информативной, с точки зрения, определения динамических свойств системы управления является переходная функция. С ее помощью можно оценить качества переходного процесса, то, как он зависит от внешнего воздействия (нагрузки). Статизм или астатизм системы по отношению к управляющим воздействиям и соответственно значение ошибки системы при отработке ею заданного сигнала после окончания переходного процесса. По виду переходной функции можно определить является ли система устойчивой, или нет.
Переходной функцией (характеристикой) (ПФ, ПХ) системы называется реакция системы на единичное ступенчатое воздействие 
при нулевых начальных условиях (для нее существует специальное обозначение 
). Поскольку изображение ступенчатого воздействия имеет вид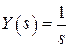 
, то соответственно имеем 
, или 
.
Вид переходной функцией определяется расположением полюсов передаточной функции системы управления.
В зависимости от их расположения на комплексной плоскости можно выделить следующие типы переходных функций (процессов) (рис. 1.4):
· колебательные (кривая 1), в которых имеет место два и более перерегулирований;
· малоколебательные (кривая 2), в которых число перерегулирований равно единице;
· без перерегулирования (кривая 3), в которых 
для всех 
· монотонные (кривая 4), характеризующиеся тем, что скорость изменения выхода не меняет знака в течение всего времени 
Рис. 1.4. Основные типы переходных функций (процессов)
С помощью переходной функции можно оценить качества переходного процесса, то, как он зависит от внешнего воздействия (нагрузки), статизм или астатизм системы по отношению к управляющим воздействиям и соответственно значение ошибки системы при отработке ею заданного сигнала после окончания переходного процесса.
Например, если переходная функция имеет вид представленный на рис 1.5., то она является статической.
Рис. 1.5. Выходной сигнал системы при 
Если переходная функция имеет вид изображенный на рис 1.6., то она является астатической.
Рис. 1.6. Выходной сигнал системы при
По виду переходной функции можно определить является ли система устойчивой, или нет.
Переходная и импульсная переходная функции связаны соотношениями
,
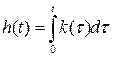или
.
Как видим, знание одной динамической характеристики позволяет определить другую. Обе динамические характеристики являются взаимосвязанными.
