RSA-ключи генерируются следующим образом:[14]
1. Выбираются два различных случайных простых числа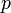 
и 
заданного размера (например, 1024 бита каждое).
2. Вычисляется их произведение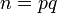 
, которое называется модулем.
3. Вычисляется значение функции Эйлера от числа 
:
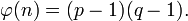
4. Выбирается целое число 
(
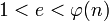), взаимно простое со значением функции 
. Обычно в качестве берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
§ Число называется открытой экспонентой (англ. public exponent)
§ Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в .
§ Слишком малые значения , например 3, потенциально могут ослабить безопасность схемы RSA.[15]
5. Вычисляется число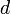 
, мультипликативно обратное к числу по модулю , то есть число, удовлетворяющее условию:
.
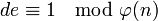§ Число 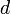называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
6. Пара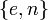 
публикуется в качестве открытого ключа RSA (англ. RSA public key).
7. Пара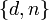 
играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.
Алгоритм шифрования:
§ Взять открытый ключ 
Алисы
§ Взять открытый текст 
§ Зашифровать сообщение с использованием открытого ключа Алисы:
Алгоритм расшифрования:
§ Принять зашифрованное сообщение 
§ Взять свой закрытый ключ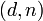 
§ Применить закрытый ключ для расшифрования сообщения:
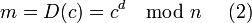
22. Схема шифрования “цифровой конверт”.
Цифровой конверт -Данные, добавляемые в конце сообщения и позволяющие определенному получателю проверить целостность содержания сообщения
Асимметричные алгоритмы позволяют легко обменяться ключами шифрования по открытому каналу связи - но работают слишком медленно. Симметричные алгоритмы работают быстро - но для обмена ключами требуют наличия защищенного канала связи и, к тому же, нуждаются в частой смене ключей. Поэтому в современных криптосистемах используются сильные стороны обоих подходов. Так, для шифрования сообщения используется симметричный алгоритм со случайным ключом шифрования, действующим только в пределах одного сеанса,- сеансовым ключом. Чтобы впоследствии сообщение могло быть расшифровано, сеансовый ключ подвергается шифрованию асимметричным алгоритмом с использованием открытого ключа получателя сообщения. Зашифрованный таким образом сеансовый ключ сохраняется вместе с сообщением, образуя цифровой конверт. При необходимости цифровой конверт может содержать сеансовый ключ в нескольких экземплярах - зашифрованный открытыми ключами различных получателей.
23. ЭЦП. Классическая схема.
Электро́нная по́дпись (ЭП) — информация в электронной форме, которая присоединена к другой информации в электронной форме (подписываемой информации) или иным образом связана с такой информацией и которая используется для определения лица, подписывающего информацию
Алгоритм шифрования:
§ Взять открытый текст
§ Создать цифровую подпись 
с помощью своего секретного ключа :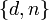
§ Передать пару 
, состоящую из сообщения и подписи.
Алгоритм расшифрования:
§ Принять пару
§ Взять открытый ключ 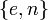Алисы
§ Вычислить прообраз сообщения из подписи:
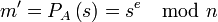
§ Проверить подлинность подписи (и неизменность сообщения), сравнив и 
24. Функция хэширования. Ее свойства.
Хеширование (иногда х э ширование, англ. hashing) — преобразование входного массива данных произвольной длины в выходную битовую строку фиксированной длины. Такие преобразования также называются хеш-функциями или функциями свёртки, а их результаты называют хешем, хеш-кодом или дайджестом сообщения (англ. message digest).
Хеширование применяется для сравнения данных: если у двух массивов хеш-коды разные, массивы гарантированно различаются; если одинаковые — массивы, скорее всего, одинаковы. В общем случае однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов входного массива; существует множество массивов, дающих одинаковые хеш-коды — так называемые коллизии. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций.
Существует множество алгоритмов хеширования с различными характеристиками (разрядность, вычислительная сложность, криптостойкость и т. п.). Выбор той или иной хеш-функции определяется спецификой решаемой задачи. Простейшими примерами хеш-функций могут служить контрольная сумма или CRC.
Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии. Для того чтобы хеш-функция H считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:
§ Необратимость: для заданного значения хеш-функции m должно быть вычислительно неосуществимо найти блок данных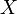 
, для которого 
.
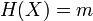§ Стойкость к коллизиям первого рода: для заданного сообщения M должно быть вычислительно неосуществимо подобрать другое сообщение N, для которого 
.
§ Стойкость к коллизиям второго рода: должно быть вычислительно неосуществимо подобрать пару сообщений 
, имеющих одинаковый хеш.
Данные требования не являются независимыми:
§ Обратимая функция нестойка к коллизиям первого и второго рода.
§ Функция, нестойкая к коллизиям первого рода, нестойка к коллизиям второго рода; обратное неверно.
Следует отметить, что не доказано существование необратимых хеш-функций, для которых вычисление какого-либо прообраза заданного значения хеш-функции теоретически невозможно. Обычно нахождение обратного значения является лишь вычислительно сложной задачей.
Атака «дней рождения» позволяет находить коллизии для хеш-функции с длиной значений n битов в среднем за примерно 
вычислений хеш-функции. Поэтому n -битная хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для неё близка к .
Для криптографических хеш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось (лавинный эффект). В частности, значение хеша не должно давать утечки информации даже об отдельных битах аргумента. Это требование является залогом криптостойкости алгоритмов хеширования, хеширующих пользовательский пароль для получения ключа.
25. Идентификация и аутентификация.
Идентификация в информационных системах — присвоение субъектам и объектам идентификатора и / или сравнение идентификатора с перечнем присвоенных идентификаторов[1]. Например, идентификация по штрихкоду.
Аутентифика́ция (англ. Authentication) — процедура проверки подлинности[1], например: проверка подлинности пользователя путём сравнения введённого им пароля с паролем в базе данных пользователей; подтверждение подлинности электронного письма путём проверки цифровой подписи письма по ключу шифрования отправителя; проверка контрольной суммы файлана соответствие сумме, заявленной автором этого файла. В русском языке термин применяется в основном в сфере информационных технологий.
Учитывая степень доверия и политику безопасности систем, проводимая проверка подлинности может быть односторонней или взаимной. Обычно она проводится с помощьюкриптографических методов.
Аутентификацию не следует путать с авторизацией[2] (процедурой предоставления субъекту определённых прав) и идентификацией (процедурой распознавания субъекта по его идентификатору).
26. Угрозы безопасности парольных систем.
