Режим гаммирования позволяет злоумышленнику воздействовать на исходный текст путем изменения битов шифрованного текста, т.к. шифрование производится побитово. Изменив один бит в зашифрованном тексте на противоположный получим изменение того же бита в расшифрованном тексте. Гаммирование с обратной связью позволяет зацепить блоки один за другой и любое изменение хотя бы одного бита в каком-либо месте шифртекста повлечет за собой при расшифровке повреждение информации во всех последующих блоках, что легко заметить.
Гаммирование с обратной связью отличается от простого гаммирования тем, что очередной элемент гаммы вырабатывается как результат преобразования по циклу зашифрования предыдущего блока зашифрованных данных, а для зашифрования первого блока массива данных элемент гаммы вырабатывается как результат преобразования по тому же циклу синхропосылки. На стойкость шифра зацепление блоков не оказывает никакого влияния.
17. Режим выработки имитовставки в ГОСТ 28147-89.
Выработка имитовставки
Имитовставка – это контрольная комбинация, зависящая от открытых данных и секретной ключевой информации. Целью использования имитовставки является обнаружение всех случайных или преднамеренных изменений в массиве данных. Для потенциального злоумышленника две следующие задачи практически неразрешимы, если он не владеет ключевой информацией: вычисление имитовставки для заданного открытого массива данных; подбор открытых данных под заданную имитовставку. Алгоритм выработки имитовставки:
· S = 0.
· Для каждого 64-битного блока данных из массива данных: S = F(S xor Ti), где Ti - блок данных, F - базовый цикл выработки имитовставки (16-З), xor - операция исключающего или.
· S - полученная имитовставка.
В качестве имитовставки можно использовать лишь часть полученного числа S, но следует помнить, что вероятность успешного навязывания ложных данных равна величине 2-L, где L - длина используемой части числа в битах. Обычно используются младшие 32 бита числа S.
18. Алгоритм шифрования Rijndael. Число циклов. Общая схема шифрования.
Advanced Encryption Standard (AES), также известный как Rijndael (произносится [rɛindaːl]) — симметричный алгоритм блочного шифрования (размер блока 128 бит, ключ 128/192/256 бит), принятый в качестве стандарта шифрования правительством США по результатам конкурса AES. Этот алгоритм хорошо проанализирован и сейчас широко используется, как это было с его предшественникомDES. Национальный институт стандартов и технологий США (англ. National Institute of Standards and Technology, NIST) опубликовал спецификацию AES 26 ноября 2001 года после пятилетнего периода, в ходе которого были созданы и оценены 15 кандидатур. 26 мая 2002 года AES был объявлен стандартом шифрования. По состоянию на 2009 год AES является одним из самых распространённых алгоритмов симметричного шифрования.[1][2] Поддержка AES (и только его) введена фирмой Intel в семейство процессоров x86 начиная с Intel Core i7-980X Extreme Edition, а затем на процессорах Sandy Bridge.
Структура алгоритма
Алгоритм AES представляет блок данных в виде двумерного байтового массива размером 4×4. Все операции производятся над отдельными байтами массива, а также над независимыми столбцами и строками.
В каждом раунде алгоритма выполняются следующие преобразования (рис. 3.7) [132, 153]:
1. Операция SubBytes, представляющая собой табличную замену каждого байта массива данных согласно табл. 3.1 (рис. 3.8).
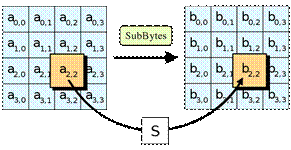
В процедуре SubBytes, каждый байт в state заменяется соответствующим элементом в фиксированной 8-битной таблице поиска, S; bij = S(aij).
2. Операция ShiftRows, которая выполняет циклический сдвиг влево всех строк массива данных, за исключением нулевой (рис. 3.9). Сдвиг /-й строки массива (для i = 1,2,3) производится на / байтов.
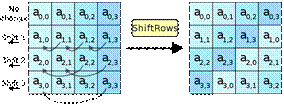
В процедуре ShiftRows, байты в каждой строке state циклически сдвигаются влево. Размер смещения байтов каждой строки зависит от её номера
3. Операция MixColumns. Выполняет умножение каждого столбца массива данных (рис. 3.10), который рассматривается как полином в конечном поле GF(28), на фиксированный полином а(х):
а(х) = 3х3 + х2 + х + 2.
Умножение выполняется по модулю х4 + 1.
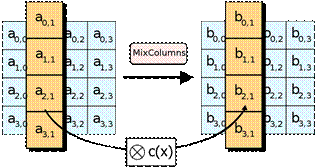
В процедуре MixColumns, каждая колонка состояния перемножается с фиксированным многочленом c(x).
- Операция AddRoundKey. Выполняет наложение на массив данных материала ключа. А именно, на /-й столбец массива данных (/ = 0…3) побитовой логической операцией «исключающее или» (XOR) накладывается определенное слово расширенного ключа W4r+i, гдег— номер текущего раунда алгоритма, начиная с 1 (процедура расширения ключа будет описана далее). Операция AddRoundKey представлена на рис. 3.11.
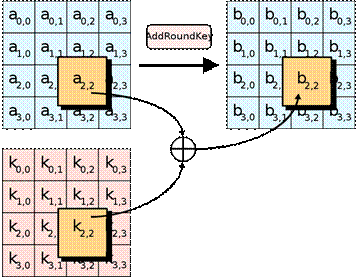
В процедуре AddRoundKey, каждый байт состояния объединяется с RoundKey используя операцию XOR (⊕).
19. Стеганографическая защита данных.
Стеганогра́фия (от греч. στεγανός — скрытый + γράφω — пишу; буквально «тайнопись») — это наука о скрытой передаче информации путём сохранения в тайне самого факта передачи. Этот термин ввел в 1499 году Иоганн Тритемий в своем трактате «Стеганография» (Steganographia), зашифрованным под магическую книгу.
В отличие от криптографии, которая скрывает содержимое секретного сообщения, стеганография скрывает сам факт его существования. Как правило, сообщение будет выглядеть как что-либо иное, например, как изображение, статья, список покупок, письмо или судоку. Стеганографию обычно используют совместно с методами криптографии, таким образом, дополняя её.
Преимущество стеганографии над чистой криптографией состоит в том, что сообщения не привлекают к себе внимания. Сообщения, факт шифрования которых не скрыт, вызывают подозрение и могут быть сами по себе уличающими в тех странах, в которых запрещена криптография.[1] Таким образом, криптография защищает содержание сообщения, а стеганография защищает сам факт наличия каких-либо скрытых посланий.
Компьютерная стеганография — направление классической стеганографии, основанное на особенностях компьютерной платформы. Примеры — стеганографическая файловая система StegFS для Linux, скрытие данных в неиспользуемых областях форматов файлов, подмена символов в названиях файлов, текстовая стеганография и т. д. Приведём некоторые примеры:
§ Использование зарезервированных полей компьютерных форматов файлов — суть метода состоит в том, что часть поля расширений, не заполненная информацией о расширении, по умолчанию заполняется нулями. Соответственно мы можем использовать эту «нулевую» часть для записи своих данных. Недостатком этого метода является низкая степень скрытности и малый объем передаваемой информации.
20. Криптография с открытым ключом. Схема выработки совместного ключа Диффи-Хеллмана.
Криптографическая система с открытым ключом (или Асимметричное шифрование, Асимметричный шифр) — система шифрования и/или электронной цифровой подписи (ЭЦП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу, и используется для проверки ЭЦП и для шифрования сообщения. Для генерации ЭЦП и для расшифровки сообщения используется секретный ключ. [1] Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL (лежащих в основе HTTPS), в SSH. Также используется в PGP, S/MIME. Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, то есть таких функций 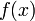 , что по известному
, что по известному 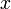 довольно просто найти значение
довольно просто найти значение 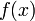 , тогда как определение
, тогда как определение 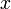 из
из 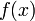 невозможно за разумный срок.
невозможно за разумный срок.
Схема выработки совместного ключа Диффи-Хеллмана.
Для заданных параметров N = 29 и g = 10 выработайте совместный секретный ключ.
1 Выберите случайное число k A, 1 < k A < N.
2 Вычислите значение y A по формуле
y A = g k A mod N.
3 Выберите случайное число k B, 1 < k B < N.
4 Вычислите значение y B по формуле
y B = g k B mod N.
5 «Обменяйтесь» значениями y A и y B.
6 Вычислите значение y BA по формуле
y BA = y B k A mod N.
7 Вычислите значение y AB по формуле
y AB = y A k B mod N.
8 Убедитесь, что значениями y AB и y BA совпадают.
21. Алгоритм шифрования RSA.
RSA (буквенная аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.
Криптосистема RSA стала первой системой, пригодной и для шифрования, и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений, включая PGP,S/MIME, TLS/SSL, IPSEC/IKE и других.[
Криптографические системы с открытым ключом используют так называемые односторонние функции, которые обладают следующим свойством:
§ Если известно 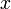 , то
, то 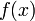 вычислить относительно просто
вычислить относительно просто
§ Если известно 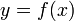 , то для вычисления
, то для вычисления 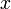 нет простого (эффективного) пути.
нет простого (эффективного) пути.
Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
В основу криптографической системы с открытым ключом RSA положена сложность задачи факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования за разумное время (обратной операции) необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложения числа на простые множители.
В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. private key). В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме RSA образуют «согласованную пару» в том смысле, что они являются взаимно обратными






