Взлом полиалфавитных шифров

Проще всего взломать полиалфавитный шифр, зная его период, то есть число используемых моноалфавитных шифров. Тогда, выбрав буквы, соответствующие каждому из моноалфавитных шифров, можно к каждому из них применить так называемый частотный анализ (или какой-нибудь другой метод взлома моноалфавитных шифров), основанный на том, что каждая буква в произвольном тексте появляется с вполне определённой частотой, а значит, посмотрев частоты появления тех или иных букв, можно узнать, как происходит замена. Одним из методов нахождения периода полиалфавитных шифров является метод, предложенный Фредериком Касиски в 1836 году. Он заключается в том, что в зашифрованном тексте находятся одинаковые сегменты длины не меньше, чем три буквы, затем вычисляются расстояния между первыми буквами соседних сегментов. Оказывается, предполагаемый период является кратным наибольшему общему делителю для этих расстояний.

8. Шифр простой замены. Криптоанализ шифра простой замены.

Шифр простой замены, простой подстановочный шифр, моноалфавитный шифр — класс методов шифрования, которые сводится к созданию по определённому алгоритму таблицы шифрования, в которой для каждой буквы открытого текста существует единственная сопоставленная ей буква шифр-текста. Само шифрование заключается в замене букв согласно таблице. Для расшифровки достаточно иметь ту же таблицу, либо знать алгоритм, по которой она генерируется.

К шифрам простой замены относятся многие способы шифрования, возникшие в древности или средневековье, как, например, Атбаш (также читается как этбаш) или Шифр Цезаря. Для вскрытия подобных шифров используется частотный криптоанализ.

Является частным случаем шифра подстановки.

Отметим, что шифр простой замены не всегда подразумевает замену буквы на какую-то другую букву. Допускается использовать замену буквы на цифру.

9. Биграммные шифры.

Бигра́ммный шифр — это криптографический алгоритм, который предназначен для шифрования групп из двух букв (биграмм).

Считается, что «отец» биграммных шифров — это немецкий аббат Иоганн Трисемус, который еще в 1508 г. в своей работе по криптологии, которая называлась «Полиграфия», впервые отметил возможность шифрования биграммами, то есть, двухбуквенными сочетаниями. Их устойчивость к вскрытию оказалась намного выше, чем у других предшественников, поэтому некоторые биграммные шифры сохранили свою актуальность вплоть до Второй мировой войны.

Биграммный «Шифр Плейфера» использовался Великобританией в годы Первой мировой войны.

Биграммный шифр «Двойной квадрат» был изобретен англичанином Чарльзом Уитстоном в 1854 году, и даже использовался немцами в годы Второй мировой войны.

Шифр Плейфера или квадрат Плейфера — ручная симметричная техника шифрования, в которой впервые использована замена биграмм. Изобретена в 1854 году Чарльзом Уитстоном, но названа именем Лорда Лайона Плейфера, который внедрил данный шифр в государственные службы Великобритании. Шифр предусматривает шифрование пар символов (биграмм) вместо одиночных символов, как в шифре подстановки и в более сложных системах шифрования Виженера. Таким образом, шифр Плейфера более устойчив к взлому по сравнению с шифром простой замены, так как затрудняется частотный анализ. Он может быть проведен, но не для 26 возможных символов (латинский алфавит), а для 26х26=676 возможных биграмм. Анализ частоты биграмм возможен, но является значительно более трудным и требует намного большего объема зашифрованного текста.

10. Шифр перестановки.

Шифр перестановки — шифр, переставляющий символы сообщения между собой для получения шифротекста, так что символы, оставаясь сами собой меняют свою позицию в сообщении.

В этой категории шифров самым интересным является так называемый „шифр нигилистов“.

При помощи пробуравленных патронов Флейснера достигается большое разнообразие замещений. При пользовании такого рода прибором буквы наносятся на бумагу посредством отверстий патронов. Как только все отверстия использованы, патрон поворачивают на 90°, и тогда вновь можно размещать буквы по свободным клеткам. Отверстия патронов устроены с таким расчетом, что после 4-кратного поворота патрона не могут занять места против клеток, уже заполненных буквами. Письмо в окончательном виде располагается правильной фигурой, но неразборчиво, и может быть дешифровано лишь владельцем точно такого же патрона.

11. Криптографическая защита информации. Потоковые и блочные шифры. Шифр Вернама.

Блочный шифр — разновидность симметричного шифра. В отличие от поточного, блоковый шифр обрабатывает открытый текст блоками по несколько (как правило 8 или 16) байт за однуитерацию. Если исходный текст (или его остаток) меньше размера блока, перед шифрованием его дополняют. Преобразование должно использовать следующие принципы:

§ Рассеивание (diffusion) — то есть изменение любого знака открытого текста или ключа влияет на большое число знаков шифротекста, что скрывает статистические свойства открытого текста;

§ Перемешивание (confusion) — использование преобразований, затрудняющих получение статистических зависимостей между шифротекстом и открытым текстом.

К достоинствам блочных шифров относят похожесть процедур шифрования и расшифрования, которые, как правило, отличаются лишь порядком действий. Это упрощает создание устройств шифрования, так как позволяет использовать одни и те же блоки в цепях шифрования и расшифрования.

Пото́чный шифр — это симметричный шифр, в котором каждый символ открытого текста преобразуется в символ шифрованного текста в зависимости не только от используемого ключа, но и от его расположения в потоке открытого текста. Поточный шифр реализует другой подход к симметричному шифрованию, нежели блочные шифры.

Шифр Вернама (другое название: англ. One-time pad — схема одноразовых блокнотов) — в криптографии система симметричного шифрования, изобретённая в 1917 году сотрудникамиAT&T Мейджором Джозефом Моборном и Гильбертом Вернамом. Шифр Вернама является системой шифрования, для которой доказана абсолютная криптографическая стойкость. Для произведения шифротекста открытый текст объединяется операцией «исключающее ИЛИ» с ключом (называемым одноразовым блокнотом или шифроблокнотом). При этом ключ должен обладать тремя критически важными свойствами:

1. быть истинно случайным;

2. совпадать по размеру с заданным открытым текстом;

3. применяться только один раз.

Шифр назван в честь телеграфиста AT&T Гильберта Вернама, который в 1917 году построил телеграфный аппарат, который выполнял эту операцию автоматически — надо было только подать на него ленту с ключом. Не будучи шифровальщиком, тем не менее, Вернам верно заметил важное свойство своего шифра — каждая лента должна использоваться только один раз и после этого уничтожаться. Это трудноприменимо на практике — поэтому аппарат был переделан на несколько закольцованных лент с взаимно простыми периодами.

12. Генераторы случайных чисел. Мультипликативный конгруэнтный генератор.

Генератор псевдослучайных чисел (ГПСЧ, англ. Pseudorandom number generator, PRNG) — алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Современная информатика широко использует псевдослучайные числа в самых разных приложениях — от метода Монте-Карло и имитационного моделирования до криптографии. При этом от качества используемых ГПСЧ напрямую зависит качество получаемых результатов. Это обстоятельство подчёркивает известный афоризм Роберта Р. Кавью из ORNL (англ.): «генерация случайных чисел слишком важна, чтобы оставлять её на волю случая».

Мультипликативный конгруэнтный метод. В качестве текущего значения случайного числа выделяют остаток от деления произведения предыдущего случайного числа и постоянного множителя a на постоянное число m:

yi=a*yi-1*(mod m),

где a, m -постоянные числа; yi - случайное число.

13. Стандарт шифрования ГОСТ 28147-89. Общая схема шифрования в режиме простой замены.

ГОСТ 28147-89 — советский и российский стандарт симметричного шифрования, введённый в 1990 году, также является стандартом СНГ. Полное название — «ГОСТ 28147-89 Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования». Блочный шифроалгоритм. При использовании метода шифрования с гаммированием, может выполнять функции поточного шифроалгоритма.

ГОСТ 28147-89 — блочный шифр с 256-битным ключом и 32 циклами преобразования, оперирующий 64-битными блоками. Основа алгоритмашифра — Сеть Фейстеля. Базовым режимом шифрования по ГОСТ 28147-89 является режим простой замены (определены также более сложные режимы гаммирование, гаммирование с обратной связью и режим имитовставки). Для зашифрования в этом режиме открытый текст сначала разбивается на две половины (младшие биты — A, старшие биты — B^[2]). На i-ом цикле используется подключ K_i:

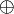( = двоичное «исключающее или»)

Для генерации подключей исходный 256-битный ключ разбивается на восемь 32-битных блоков: K₁…K₈.

Ключи K₉…K₂₄ являются циклическим повторением ключей K₁…K₈ (нумеруются от младших битов к старшим). Ключи K₂₅…K₃₂ являются ключами K₁…K₈, идущими в обратном порядке.

После выполнения всех 32 раундов алгоритма, блоки A₃₃ и B₃₃ склеиваются (обратите внимание, что старшим битом становится A₃₃, а младшим — B₃₃) — результат есть результат работы алгоритма.

Расшифрование выполняется так же, как и зашифрование, но инвертируется порядок подключей K_i.

14. Функция преобразования f(R_i,X_i) в алгоритме ГОСТ 28147-89.

Функция 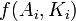вычисляется следующим образом:

A_i и K_i складываются по модулю 2³².

Результат разбивается на восемь 4-битовых подпоследовательностей, каждая из которых поступает на вход своего узла таблицы замен (в порядке возрастания старшинства битов), называемого ниже S-блоком. Общее количество S-блоков ГОСТа — восемь, то есть столько же, сколько и подпоследовательностей. Каждый S-блок представляет собой перестановку чисел от 0 до 15. Первая 4-битная подпоследовательность попадает на вход первого S-блока, вторая — на вход второго и т. д.

Если S-блок выглядит так:

1, 15, 13, 0, 5, 7, 10, 4, 9, 2, 3, 14, 6, 11, 8, 12

и на входе S-блока 0, то на выходе будет 1, если 4, то на выходе будет 5, если на входе 12, то на выходе 6 и т. д.

Выходы всех восьми S-блоков объединяются в 32-битное слово, затем всё слово циклически сдвигается влево (к старшим разрядам) на 11 битов.

 

15. Алгоритм расшифрования ГОСТ 28147-89. Общая схема. Формирование ключей в алгоритме шифрования ГОСТ 28147-89.

Для генерации подключей исходный 256-битный ключ разбивается на восемь 32-битных блоков: K₁…K₈.

Ключи K₉…K₂₄ являются циклическим повторением ключей K₁…K₈ (нумеруются от младших битов к старшим). Ключи K₂₅…K₃₂ являются ключами K₁…K₈, идущими в обратном порядке.

После выполнения всех 32 раундов алгоритма, блоки A₃₃ и B₃₃ склеиваются (обратите внимание, что старшим битом становится A₃₃, а младшим — B₃₃) — результат есть результат работы алгоритма.

Расшифрование выполняется так же, как и зашифрование, но инвертируется порядок подключей K_i.

16. Режимы гаммирования и гаммирования с обратной связью в ГОСТ 28147-89.

Гаммирование

Суть гаммирования состоит в том, чтобы не шифровать сами данные, а шифровать некоторые случайные или псевдослучайные числа, вырабатываемые специальным программным или аппаратным генератором и накладывать получившуюся гамму на массив данных с помощью операции исключающего или. При этом операция зашифрования ничем не отличается от операции расшифрования, т.к. наложение той же гаммы на массив данных два раза подряд дает исходный массив данных без искажений.

Для выработки случайных 64-битных чисел в ГОСТ 28147-89 определен специальный математический генератор, который будет рассмотрен чудь позже. Т.о. шифрование и расшифровка данных в режиме гаммирования производится путем наложения зашифрованных псевдослучайных чисел.

У этого и следующего режимов есть интересная особенность: т.к. генератор псевдослучайных чисел необходимо инициализировать начальным 64-битным значением, в качестве которого очень часто используется текущее время зашифровки, то в разное время при шифровании одного и того же массива данных под один и тот же пароль можно получить разные шифртексты! При этом значение, которым был проинициализирован генератор посылается получателю вместе с массивом зашифрованных данных и называется синхропосылкой или начальным заполнителем по терминологии ГОСТа.

Замечу, что ГОСТ 28147-89 определяет в качестве синхропосылки или начального заполнителя не само число, полученное из какого-либо источника (например, текущее время), а результат зашифровки этого числа по алгоритму зашифрования. Т.о. используя текущее время или что-то иное в качестве начального заполнителя необходимо это число предварительно зашифровать, а затем уже инициализировать им генератор.

Рекуррентный генератор последовательности чисел (РГПЧ)

Это и есть тот самый генератор чисел, который используется при шифровании гаммированием. На каждом шаге он выдает 64-битное число, которое по сути состоит из двух 32-битных чисел, которые генерируются по-отдельности. Фактически существуют два РГПЧ для старшей и младшей частей.