Дисперсионный анализ был разработан в 20-х годах ХХ-го столетия английским математиком и генетиком Рональдом Фишером.
Это метод анализа для сравнения средних более чем двух групп. В центре внимания метода находится дисперсия, то есть мера изменчивости признаков.
Базовая идея Д.А. заключается в разложении общей диперсии изучаемых признаков на сооставляющие. Д.А. являетсяпараметрическим методом и предполагает, что выборки извлечены из совокупности, распределенной по нормальному закону.
Д.А. позволяет ответить на вопрос, равны ли все сравниваемые средние.
ОПРЕДЕЛЕНИЕ: То, что оказывает влияние на конечный результат, называется фактором или факторами если их несколько.
ОПРЕДЕЛЕНИЕ: Конкретную реализацию фактора называют уровнем фактора.
ОПРЕДЕЛЕНИЕ: Значение измеряемого признака называют откликом.
Для сравнения влияния факторов на результат необходим определенный статистический материал. Обычно его получают следующим образом: каждый k способов обработки применяют несколько раз к исследуемому объекту и регистрируют результаты. Итогом подобных испытаний являются k выборок разных объемов.
ОПРЕДЕЛЕНИЕ: Дисперсионным анализом называют группу статистических методов предназначенных для исследования двух и более выборок путем сравнения выборочных дисперсий.
ОПРЕДЕЛЕНИЕ: В зависимости от количества изучаемых факторов различают однофакторный и многофакторный дисперсионные анализы.
Дисперсионный анализ применяют для изучения влияния факторов, характеризующихся несколькими уровнями.
Пусть имеются генеральные совокупности X1,X2,…,Xk такие что
- все k генеральных совокупностей распределены нормально;
- дисперсии всех генеральных совокупностей одинаковы.
При этих условиях и заданном уровне значимости α требуется проверить нулевую гипотезу равенства средних.
H0: 
(1)
Таким образом, извлекая из каждой генеральной совокупности по выборке, требуется установить значимость или незначимость различия полученных k выборочных средних.
Можно предполагать, что все k генеральных совокупностей в чистом виде идентичны, т.е. имеют не только равные дисперсии, но и одинаковые средние значения. Однако каждая из генеральных совокупностей подвержена влиянию одного или нескольких качественных факторов, входящих в эксперимент, которые могут изменять средние значения наших генеральных совокупностей.
Основная идея дисперсионного анализа состоит в разбиении этой выборочной дисперсии на две компоненты, одна из которых соответствует влиянию фактора на изменчивость средних значений (факторная дисперсия), а вторая обусловлена случайными причинами и не влияет на изменчивость средних (остаточная дисперсия).
ОПРЕДЕЛЕНИЕ: Выборочная дисперсия которая соответствует влиянию фактора на изменчивость средних значений называется факторной дисперсией.
ОПРЕДЕЛЕНИЕ: Выборочная дисперсия, обусловленная случайными причинами и не влияющая на изменчивость средних называется остаточной дисперсией.
Дальнейшее сравнение с помощью критерия Фишера этих компонент позволяет численно оценить влияние исследуемого фактора.
| Источник вариации, дисперсии | Сумма квадратов (отклонений) | Число степеней свободы | Средний квадрат MS | 
| 
|
| Межгрупповая (фактор А) |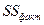 
| k-1 | 
| 
| 
|
| Внутригрупповая (остаточная) |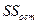 
| k(r-1) | 
| ||
| Общая | 
| kr-1 | 
|
В случае нескольких факторов идея дисперсионного анализа остается той же (сравнение факторных и остаточной дисперсий), но усложняется.
ОПРЕДЕЛЕНИЕ: Общей суммой квадратов отклонений называют сумму
(3)
где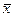 
общая средняя для всей выборки объема n.
ОПРЕДЕЛЕНИЕ: Факторной суммой квадратов отклонений называют сумму
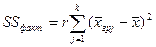(4)
Сумма 
характеризует отклонения групповых средних.
ОПРЕДЕЛЕНИЕ: Остаточной суммой квадратов отклонений называют сумму
(5)
Сумма 
характеризует степень рассеяния значений внутри групп.
Смысл введенных SS:
Если фактор А на каком –то уровне оказывает влияние на признак Х, то в выборке, соответствующей этому уровню, он изменяет групповую среднюю, и эта групповая средняя будет отличаться от общей средней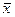 
тем сильнее, чем больше воздействие фактора. А чем больше различие групповой средней и общей средней, тем больше и величина . Оказывается, имеет место прямая зависимость степени воздействия фактора и величины .
Для введенных сумм квадратов справедливо равенство.
(6)
Для исследования влияния фактора на групповые средние можно использовать найденные суммы квадратов отклонений, однако более удобным представляется переход от SS к средним квадратам отклонений. Средний квадрат принято обозначать MS(Mean Sqare).
-общая дисперсия (7)
где n-1 число степеней свободы, n -суммарное количество значений во всех к группах.
- факторная дисперсия (8)
где к-1 число степеней свободы, к- количество групп (количество уровней фактора)
остаточная дисперсия (9)
где к(r-1) число степеней свободы для , к -количество групп, r -количество значений в каждой группе.
Для вычисления SS формулы можно преобразовать к более простому виду.
где 
, 
(10)
(11)
(12)
Методика проведения дисперсионного анализа.
- Формулируем нулевую и альтернативную гипотезы:
Н0: групповые генеральные средние равны a1=a2=…=ak, а также различие выборочных средних получилось случайно, реального влияния фактор не оказывает
H1: различие между выборочными средними не случайно и обусловлено влиянием фактора.
2. Задается уровень значимости α (например, α=0,05 или α=0,01)
3. Вычисляются 
и 
Если 
, то признается нулевая гипотеза
Если 
, то вычисляется функция 
(статистика, которая имеет распределение Фишера)
4. После вычисления находится по таблицам критических значений распределения Фишера.
должно соответствовать числам степеней свободы k-1 и k(r-1) соответственно.
5. Сравниваются и . Если < , то при заданном уровне значимости нулевая гипотеза Н0 принимается и делают вывод, что фактор не влияет существенно на средние значения. Если > , то нулевая гипотеза отвергается и влияние фактора признается существенным.
6. Таким образом, поведение статистики F, являющейся критерием, напрямую связано с принятием или отвержением нулевой гипотезы о равенстве средних, расчитанных по выборкам. Также отметим, что критерий F называют дисперсионным отношением. Результат дисперсионного анализа сводят в таблицу.
Таблица дисперсионного анализа
Пример: Влияние курения на заболеваемость дыхательных путей.
Среди взрослого населения определенной возрастной категории фиксировалось число заболеваний дыхательных путей за два года. Цель исследования статистическое доказательство влияния курения на заболеваемость органов дыхания. Случайным образом были отобраны 3 группы по 4 человека каждая, из них: І-группа-некурящие; ІІ- стаж курильщика до 5 лет, ІІІ группа-стаж курильщика более 5 лет.
Таким образом, исследуемый фактор А-курение, уровни фактора, А1 А2 А3 –стаж курильщика. Отклик на фактор курения –число заболеваний дыхательных путей. Были получены 12 значений количества заболеваний- это значения хij, где j-номер уровня фактора (j=1,2,3), i-номер элемента в соответствующей выборке, i=1,2,3,4:
(16)
Предполагаем, что 
выборка из нормальной генеральной совокупности.
Проведем дисперсионный анализ для установления влияния фактора курения на заболеваемость органов дыхания.
- Формулируем гипотезы:
H0- курение не влияет на заболеваемость органов дыхания
H1-курение существенно влияет на заболеваемость органов дыхания.
Таблица 1
| Номер испытания | Уровень фактора | ||
| A1 | A2 | A3 | |
T1=4
R1=6
| T2=8
R2=18
| T3=15
R3=59
|
2. Для вычисления SS используем формулы (3-5) или (10-12).
| 1 метод | 2 метод |
T1=1+0+1+2=4
T2=3+2+2+1=8
T3=3+4+5+3=15
R1=12+02+12+22=6
R2=32+22+22+12=18
R3=32+42+52+32=59
R=6+18+59=83
Тогда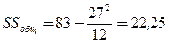    
 
| 
 
 
|
, 
Найдем число степеней свободы для каждой суммы квадратов MS по формулам (7-9).
Полученные значения занесем в таблицу дисперсионного анализа (таблица 4), в которой также кстати привести наблюдаемое и критическое значения критерия Ғ.
Число степеней свободы для 
: n-1=12-1=11
: k-1=2
: k(r-1)=3(4-1)=9
Составим таблицу
Таблица 2
| Источник вариации | Сумма квадратов SS | Число степеней свободы df | Средний квадрат MS | 
| 
|
| Межгрупповая (фактор А) Случайные отклонения (остаточная) | 15,5 6,75 | 7,75 0,75 | 
| 
| |
| Общая | 22,25 | - |
Как видим из таблицы, значения критерия , оказалось большим, чем , как при уровне значимости α=0,05, так и при α=0,01, то есть наблюдаемое значение критерия попало в критическую область, и, следовательно,нулевую гипотезу о равенстве групповых средних нужно отвергнуть. Вывод: фактор курения значимо влияет на заболеваемость дыхательных путей.
Задание. Получены следующие данные о плодовитости мышей при облучении рентгеновыми лучами:
| Группы | Число мышат от отдельных самок | |||
| Контроль | ||||
| Доза 100 р | ||||
| Доза 200 р |
Влияет ли облучение на плодовитость мышей?
