Функция (отображение) как бинарное отношение. Область определения и область значения функций. Образ и прообраз подмножества при отображении.

Фундаментальную роль в математике играет понятие функции (отображения), которое является частным случаем функционального отношения.

Определение 1. Бинарное отношение f между элементами множеств А и В (то есть ) называется функциональным отношением, если из и

Из определения 1 следует, что бинарное отношение является функциональным, когда каждому значению первой координаты пары из f соответствует единственная вторая координата, которая обозначается через y=f(x). И говорят в этом случае, что y является функцией от x.

Определение 2. называется областью определения функционального отношения.

Определение 3. Функциональное отношение f между элементами множеств А и В называется функцией или отображением А в В, если и обозначается

Множество А называется областью определения функции, множество В -областью значения функции.

Если y=f(x), то y называется образом при отображении f точки x, а x называется прообразом при отображении f точки y.

Пусть , тогда называется образом множества (подмножества) М при отображении f. В частности, образ множества А при отображении f.

Пусть тогда 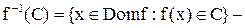прообраз множества С при отображении f. В частности,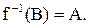

Примеры: следующие отношения являются отображениями:

Следующие отображения не являются отображениями:

 

Композиция функций. Теорема об ассоциативности произведения функций.

Определение 1. Пусть f и g – функции, причем g: A→B, f: B→C. Композицией (суперпозицией, произведением) функций f и g называется отображение A в C, значением которого для произвольного служит f(g(x)).

Обозначение: или , то есть (fg)(x)=f(g(x)).

Определение 2. Отображение и называется равными тогда и только тогда, когда f(x)=g(x)

 

Пример: Пусть и – функции, определяемые следующим образом:

; g(x)=1–x. Тогда

;

Из примера видно, что .

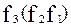Теорема 1: Пусть , и – отображения. Тогда и - отображения A в D, причем (1), то есть произведения отображений ассоциативно

Доказательство. имеем:

Следовательно, равенство (1) справедливо. Что и требовалось доказать.

 

Тождественное отображение множества на себя. Обратимое отображение. Сюръекция, инъекция, биекция. Доказательство инъективности f и сюрьективности g, удовлетворяющих условию. Теорема об обратимом отображении.

Определение 1: Отображение называется преобразованием множества A.

Определение 2: Преобразование 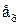множества X называется тождественным или единичным преобразованием, если , то есть преобразование 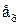каждую точку из X переводит в себя.

Определение 3: Пусть и . Если (1), то g называется левым обратным отображением для f. Если (2), то g называется правым обратным отображением для f. Если выполняются равенства (1) и (2) одновременно, то g называется обратным отображением для f.

Если для f существует обратное отображение g, то f называется обратимым отображением.Обозначение: .

Лемма 1. Пусть f – отображение X в Y. Тогда и .

Доказательство. имеем:

.

Аналогично доказывается второе равенство.

Лемма 2. Если обратное отображение для f существует, то оно единственное.

Доказательство: Пусть и пусть и – обратные отображения для f (здесь и ). Тогда для g и выполняются равенства:

и (5)

Тогда, по лемме 1, имеем: то есть .

Определение 4. Отображение называется сюръективным отображением или сюръекцией, если Imf = B. То есть сюръекция – это отображение “на” B,

Определение 5. Отображение , называется инъективным отображением (инъекцией) или взаимно однозначным отображением A в B, если из , то есть различные точки из A отображаются при f в различные точки из B.

Определение 6. Отображение называется биективным отображением (биекцией) или взаимно однозначным соответствием, если f сюръективно и инъективно.

Лемма 3: Если и и (1), то f – инъекция и g – сюръекция.

Доказательство: Покажем, что f – инъекция.

Пусть Предположим, что (*). Тогда, , то есть и, значит, f– инъективно.

Покажем, что g – сюръекция. имеем:

, то есть существует и значит, g - сюръекция.

Теорема 1. Отображение обратимо тогда и только тогда, когда f – биекция.

Доказательство. 1)Необходимость.

Пусть f – обратимо, тогда для f существует обратная функция g: (1) и (2). Из (1) по лемме 3 следует, что f – инъекция. Из (2) по лемме 3 следует, что f – сюръекция.

2)Достаточность.

Пусть f – биекция. Покажем, что f является обратимым отображением. Так как f – биекция, то – f инъекция (то есть различным точкам х₁, х₂ Х соответствуют различные точки из Y) и f – сюръекция (то есть f(Х)=Y).

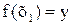Определим новое биективное отображение g по правилу Покажем, что g – функциональное отношение, то есть , g ставит в соответствие единственную точку из X. Пусть и , где . Допустим, что , тогда из инъективности f , но и . Получили противоречие следовательно, х₁=х₂.

Итак, g – функциональное отношение.

Покажем, что функциональное отношение g является отображением. Действительно, так как f – сюръекция, то 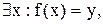а, значит,

Итак, g - отображение.

Теперь необходимо показать, что Действительно,

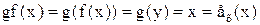и

Следовательно, g - обратная функция для f, то есть f – обратима. Что и требовалось доказать.

 

 

СОДЕРЖАНИЕ

Введение.………………………………………………………………………….
§ 1. Понятие множества, подмножества. Равенство множеств……………….
§2. Операции над множествами, их свойства…………………………………..
§3. Прямое (декартово) произведение множеств. Бинарные (n-арные) отношения, их свойства………………………………………………………….
§4. Область бинарного отношения. Операции над бинарными отношениями. ……………………………………………………………………
§ 5. Отношение эквивалентности. Теорема о разбиении множества отношением эквивалентности на классы……………………………………….
§6. Отношение порядка и предпорядка. Линейный порядок. Упорядоченные множества. Наибольший (наименьший), максимальный (минимальный) элементы упорядоченного множества……………………..
§7.Функция (отображение) как бинарное отношение. Область определения и область значения функций. Образ и прообраз подмножества при отображении…………………………………………………………………
§8. Композиция функций. Теорема об ассоциативности произведения функций…………………………………………………………………………..
§9. Тождественное отображение множества на себя. Обратимое отображение. Сюръекция, инъекция, биекция. Доказательство инъективности f и сюрьективности g, удовлетворяющих условию . Теорема об обратимом отображении…………………………………………...

 

 

 

Надежда Владимировна Силенок

 

МНОЖЕСТВА И ОТНОШЕНИЯ

Методические рекомендации по курсу «Алгебра»

 

 

Подписано в печать ___________ 2008 г. Формат 60´84 1/16

Печать офсетная. Бумага офсетная.

Усл. п. л. 1,2. Тираж 100 экз. Заказ №______

 

РИО Брянского государственного университета

Имени академика И. Г. Петровского

243036, г. Брянск, ул. Бежицкая, 14

 

 

Отпечатано в цехе полиграфии РИО БГУ