Другим важным бинарным отношением, часто встречающимся в математике, является отношение порядка.
Определение 1. Бинарное отношение 
на множестве 
Ø называется отношением порядка, если оно антисимметрично транзитивно.
Например, отношение «<» является отношением порядка на множестве N.
Определение 2. Отношение порядка на множестве А называется нестрогим, отношением порядка, если оно рефлексивно.
Например, отношение «
» является нестрогим отношением порядка на множестве N.
Определение 3. Отношение порядка на множестве А называется строгим отношением порядка, если оно антирефлексивно.
Например, отношение «<» - отношение строгого порядка на множестве N.
Определение 3 эквивалентно следующему определению:
Определение 3'. Бинарное отношение на множестве Ø называется отношением строгого порядка, если антирефлексивно и транзитивно.
Покажем, что из антирефлексивности и транзитивности на А следует антисимметричность на А.
Допустим,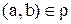 
и 
тогда, в силу транзитивности , 
, что невозможно, так как - антирефлексивно. Значит, либо 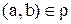, либо то есть, - антисимметрично.
Определение 4. Бинарное отношение на множестве Ø называется отношением предпорядка, если оно рефлексивно и транзитивно на А.
Определение 5. Отношение порядка на множестве А называется линейным, если оно связанно.
Определение 6. Пусть - отношение порядка на непустом множестве А. Тогда пара <А, > называется упорядоченным множеством. Если -линейный порядок, то <А, > называется линейным упорядоченным множеством.
Определение 7. Пусть <А, >-упорядоченное множество.Элемент а из А называется наименьшим (наибольшим) в А, если 
для любого элемента x из А, отличного от 
.
Определение 8. Пусть <А, > - упорядоченное множество. Элемент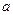 
из А называется минимальным (максимальным), в А, если выполняется условие: для любого x из а, если 
, то x = a.
Любое упорядоченное множество имеет не более одного наименьшего и не более одного наибольшего элемента, тогда, как оно может иметь несколько минимальных и максимальных элементов. В линейно упорядоченном множестве понятия наименьшего (наибольшего) и минимального (максимального) элементов совпадают.
Пример 1: пусть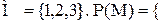 
Ø,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}. Рассмотрим на множестве Р(М) бинарное отношение «
». Это бинарное отношение рефлексивно, антисимметрично, транзитивно. Значит, оно является отношением нестрогого порядка. Отношение «» не является связанным на Р(М). Например: {1} 
{2}, но {1} 
{2} и {2} {1}. Пара 
является упорядоченным множеством, но не является линейно упорядоченным множеством. Здесь имеем единственный максимальный (он же наибольший) элемент {1,2,3} и единственный минимальный(он же наименьший) элемент Ø.
 |
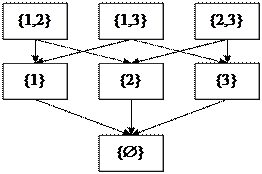
Пример 2. К={ Ø,{1},{2},{3},{1,2},{1,3},{2,3}}. <K, > - упорядоченное множество. В К наибольшего элемента нет, но в К три максимальных элемента {1,2},{1,3},{2,3}. В К единственный минимальный (он же наименьший элемент).
 |
Определение 9. Линейно упорядоченное множество <A, > называется вполне упорядоченным множеством, если каждое непустое подмножество множества А имеет наименьший элемент.
Пример 3. Если «<» - есть обычное отношение «меньше» на множестве N, то <N,< > является вполне упорядоченным множеством.
Пример 4. <R,< > - линейно упорядоченное множество, но не вполне упорядоченное множество.