Федеральное агентство по образованию РФ
БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Имени академика И. Г. Петровского
Филиал в г. Новозыбкове
кафедра математики, физики и информатики
Силенок Н. В.
МНОЖЕСТВА И ОТНОШЕНИЯ
Методические рекомендации по курсу «Алгебра»
БРЯНСК 2008
ББК 22.14я73
С - 36
Силенок Н. В. Множества и отношения. Методические рекомендации по курсу «Алгебра». – Брянск: РИО БГУ, 2008. – 20 с.
Пособие составлено в соответствии с программой курса «Алгебра» для студентов физико-математического факультета.
Рецензенты:
Анищенко А. Г. – кандидат физико-математических наук, доцент кафедры алгебры
Шубабко Е. Н. – кандидат физико-математических наук, доцент, заведующий кафедрой математики, физики и информатики филиала Брянского государственного университета в г. Новозыбкове.
Печатается по решению совета филиала Брянского государственного университета в г. Новозыбкове. Протокол №________ от _______
@ Силенок Н. В., 2008
@ РИО БГУ, 2008
Введение.
В школьном курсе математики над числами были введены некоторые отношения. Например, отношения «<», «>», «=» и др. Кроме того, некоторые отношения введены также и на других множествах. Например, на множестве всех прямых плоскости введены отношения параллельности и перпендикулярности прямых; на множестве всех треугольников плоскости введены отношения равенства и подобия треугольников и т. д.
В данном пособии изложены основные понятия теории множеств. Оно предназначено для студентов первого курса физико-математического факультета.
Понятие множества, подмножества. Равенство множеств.
Понятие множества в алгебре является первичным, т.е. неопределяемым (как например понятие точки в геометрии). Вот как Георг Кантор (1845-1918, немецкий математик) описывает понятие множества:
„Под многообразием или множеством я понимаю всякое многое, которое можно мыслить как единое, т.е. всякую совокупность определенных элементов, которая может быть связана в единое целое с помощью некоторого закона.”
Замечание: приведенная цитата не является определением множества, это его описание.
Группа французских математиков под псевдонимом Никола Бурбаки, начавшая работу в 1939г., сделала попытку обозреть всю математику с единой аксиоматической, теоретико-множественной точки зрения. У них фигурирует следующие описания понятия множества:
„Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или с элементами других множеств.”
Мы будем рассматривать интуитивную (кантовскую) теорию множеств, построенную в конце 19 в. немецким математиком Георгом Кантором.
Множества чаще всего обозначают большими буквами A, B, С,…, X, Y, а элементы множеств – малыми буквами a, b,…., α, β и т.д.
Множество, не содержащее ни одного элемента, называется пустым и обозначается Ø.
Если x есть элемент множества М, то пишут x Î М и читают „x принадлежит М”. Если x не является элементом множества М, то пишут x 
М и читают „x не принадлежит М”. Множества различают конечные и бесконечные. Конечным называется такое множество, количество элементов которого есть конечное натуральное число. Количество элементов множества А обозначается n(A) или |А|.
Определение 1. Множество В называется подмножеством множества А, если каждый элемент множества В принадлежит множеству А. Обозначение: В 
А.
Если В А и В≠А, то В называется собственным подмножеством множества А, обозначение В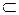 
А. Очевидно, что для любых множеств А, В и С справедливы следующие свойства:
1) А А, т. е. отношение «» - рефлексивно;
2) Если А В и В С, то А С, т. е. отношение «» - транзитивно;
3) Ø 
А.
Подмножества Ø и А множества А называются несобственными (тривиальными).
Определение 2. Два множества называются равномощными, если между их элементами можно установить взаимно однозначное соответствие, т.е. если |А|=|В|.
Определение 3. (по Кантору). Множество X называется бесконечным, если оно равномощно некоторому своему собственному подмножеству.
Символически определение 3 можно записать так:
X - бесконечно <=> 
Y 
X: |X|=|Y|.
Чаще всего для задания множеств используют два способа:
1. Перечислением всех его элементо. В этом случае элементы множества записывают внутри фигурных скобок, например: А = {1, 2, a, x} или B = {город Москва, река Десна, планета Земля}.
2. Описание множества с помощью его характеристических свойств. Чаще всего при этом используют запись A = {x: P(x)}, которую читают следующим образом: "A есть множество элементов x таких, что для них выполняется свойство P(x)".
Например, B = {x: x- натуральное число, меньшее 10 }, при этом, очевидно, что B = {1, 2, 3, 4, 5, 6, 7, 8, 9}. E = { x| x = 3k, k - любое натуральное число.}
Определение 4. Множества А и В называются равными, если каждый элемент множества А принадлежит множеству В и каждый элемент множества В принадлежит множеству А. Другими словами, множества А и В называются равными, если А является подмножеством множества В и В является подмножеством множестваА.Обозначение: А=В.
Или, символически: А=В <=> А В и В 
А.
Очевидно, чтодля любых множеств А, В и С справедливы следующие свойства:
1) Если А=В и В=С, то А=С (транзитивность отношения «=»);
2) А=А (рефлективность отношения «=»);
3) Если А=В, то В=А (симметричность отношения «=»);
Определение 5. Множество всех подмножеств заданного множества А называется булеаном множества А и обозначается Р(А).
Теорема 1. Булеан n-элементного множества А содержит 2n элементов, т.е., если │А│=n, то│Р(А)│=2n.
