Решить систему уравнений по правилу Крамера:
1.  2.
2. 
3. 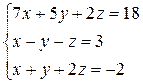
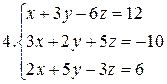







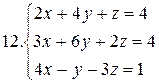

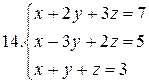
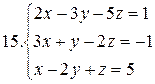




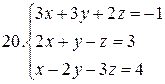

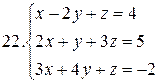


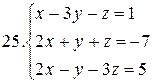 26.
26. 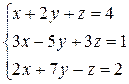
27. 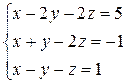



Задание № 9
Пример 12. Решить систему уравнений матричным методом
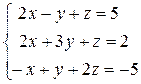 .
.
Решение. Представим данную систему в виде матричного уравнения
 , где
, где  .
.
Найдем А -1. Решение матричного уравнения имеет вид А -1× В = Х. Вычислим 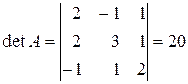 .
.
Так как det А ¹0, то матрица А имеет обратную, которая была найдена в примере №7.
 .
.
Вычислим матрицу Х:

или х = 2,55, y = – 0,75, z = – 0,85.
Примеры для самостоятельной работы
Решить систему уравнений матричным методом:
1.  2.
2. 




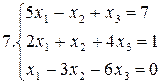
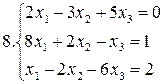







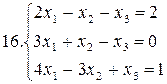



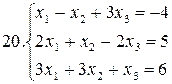


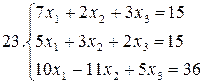

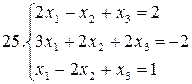 26.
26. 
27.  28.
28. 


Задание № 10
Пример 13. Решить систему уравнений методом Гаусса
 .
.
Решение. Определив первое уравнение разрешающим, перепишем систему:
 .
.
Умножим уравнение (а) на (-2) и прибавим к уравнению (б). Имеем:
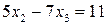 .
.
Уравнение (а) умножим на (-7) и сложим с уравнением (в) Получим:
 .
.
Составим систему уравнений:  .
.
Умножим уравнение (г) на (-3) и сложим с уравнением (д). В итоге получим:  ;
;
 ;
;
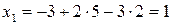 .
.
Пример 14. Решить систему методом Жордана – Гаусса:
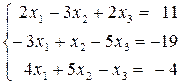 .
.
Решение. Составим расчетную таблицу, элементы которой на каждом этапе вычислений определим по правилу прямоугольника.
Правило для нахождения элементов преобразований системы, не принадлежащих разрешающим столбцу или строке, называют правилом прямоугольника.
| aij | aik | aik | bi | |||
| alj | alk | alk | bj |
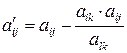 ,
,  . Таким образом, имеем следующий алгоритм преобразований:
. Таким образом, имеем следующий алгоритм преобразований:
1. элементы разрешающей строки получаются из соответствующих элементов прежней строки делением на разрешающий элемент;
2. все элементы разрешающего столбца преобразованной системы, кроме разрешающего, равны нулю;
3. все остальные элементы пересчитываются по правилу прямоугольника.
Процесс продолжается до тех пор, пока не будут использованы все уравнения системы. При этом возможны случаи.
1. В процессе исключений левая часть уравнения системы обращается в нуль, а правая часть равна некоторому числу. Это значит, что система не имеет решений, т.к. данному уравнению не могут удовлетворять никакие значения неизвестных.
2. Левая и правая части i -го уравнения обращаются в нуль. Это означает, что i -ое уравнение являются линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтому оно может быть отброшено.
3. После ряда преобразований, если число неизвестных равно числу уравнений, то система имеет единственное решение.
å - контрольный столбец, над элементами которого проводятся те же преобразования, что и над остальными элементами таблицы, при этом сумма элементов строки должна быть равна элементу контрольного столбца той же строки.
Выберем в качестве разрешающего элемента а 22 = 1. Элементы второго столбца (разрешающего) равны нулю в новой таблице, кроме а’ 22 = 1. остальные элементы пересчитываем по правилу прямоугольника.
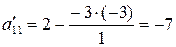 ,
, 
 ,
, 




Аналогично вычисляем последующие элементы.
| п/п | x 1 | x 2 | x 3 | своб. члены | å |
| I | -3 | ||||
| -3 | -5 | -19 | -26 | ||
| -1 | -4 | ||||
| II | -7 | -13 | -46 | -66 | |
| -3 | -5 | -19 | -26 | ||
| III | 13/7 | 46/7 | 66/7 | ||
| 4/7 | 5/7 | 16/7 | |||
| -79/7 | -237/7 | -316/7 | |||
| IV | |||||
| -1 | |||||
Из последней таблицы получаем х 1 = 1, х 2 = – 1, х 3 = 3.






