а) Вычислить определители третьего порядка:
1.  2.
2.  3.
3. 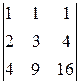
4. 
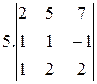 6.
6. 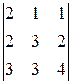
7.  8.
8.  9.
9. 
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15. 
16. 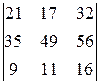 17.
17.  18.
18. 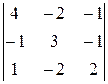
19. 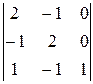 20.
20.  21.
21. 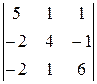
22.  23.
23.  24.
24. 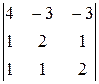
 26.
26.  27.
27. 
28. 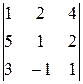 29.
29. 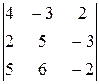 30.
30. 
б) Вычислить определители четвертого порядка:
1.  2.
2.  3.
3. 
4. 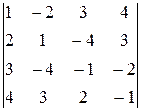 5.
5. 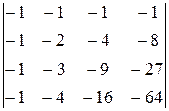 6.
6. 
7.  8.
8.  9.
9. 
10.  11.
11. 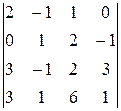 12.
12. 
13.  14.
14.  15.
15. 
16. 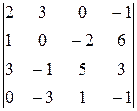 17.
17.  18.
18. 
19.  20.
20. 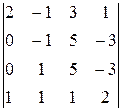 21.
21. 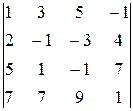
22.  23.
23.  24.
24. 
25. 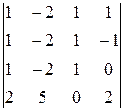 26.
26. 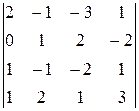 27.
27. 
28.  29.
29. 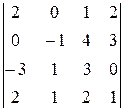 30.
30. 
Задание №4
Пример 6.Пользуясь правилом умножения матриц, представить в виде определителя произведение определителей.
Решение.

Примеры для самостоятельной работы
Пользуясь правилом умножения матриц, представить в виде определителя произведение определителей:
1.  2.
2. 
3.  4.
4. 
5. 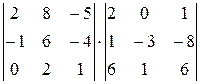 6.
6. 
7.  8.
8. 
9.  10.
10. 
11. 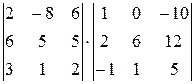 12.
12. 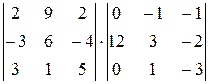
13.  14.
14. 
15.  16.
16. 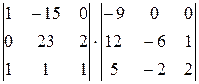
17.  18.
18. 
19.  20.
20. 
21. 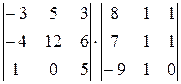 22.
22. 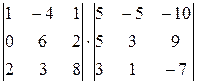
23. 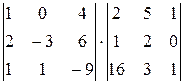 24.
24. 
25.  26.
26. 
27.  28.
28. 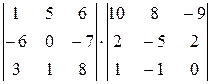
29. 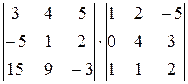 30.
30. 
Задание №5
Пример 7. Найти обратную матрицу для матрицы 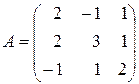 .
.
Решение. Вычислим определитель матрицы
 .
.
Определитель det А ¹0, следовательно, матрица А имеет обратную.
Составим транспонированную матрицу АТ для матрицы А:
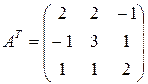 .
.
Найдем алгебраические дополнения элементов матрицы АТ:

Тогда матрица, составленная из алгебраических дополнений матрицы АТ, запишется в виде:  .
.
Запишем обратную матрицу:
 .
.
Покажем, что А × А -1= Е.
Действительно,
 .
.
Примеры для самостоятельной работы
Найти обратную матрицу для матрицы:
1.  2.
2.  3.
3. 
4.  5.
5.  6.
6. 
7.  8.
8.  9.
9. 
10. 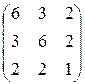 11.
11.  12.
12. 
13.  14.
14. 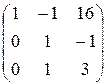 15.
15. 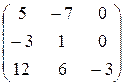
16.  17.
17.  18.
18. 
19.  20.
20.  21.
21. 
22.  23.
23.  24.
24. 
25.  26.
26.  27.
27. 
28. 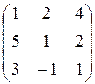 29.
29. 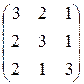 30.
30. 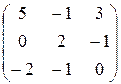
Задание № 6
Пример 8.Найти ранг матрицы.
Решение. Прибавим к четвертому столбцу первый, умноженный на (-4), затем вычеркнем 4 столбец, состоящий из нулей.
 .
.
Вычислим минор третьего порядка:  .
.
Следовательно, r (А)=3.
Примеры для самостоятельной работы
Найти ранг матрицы:
1. 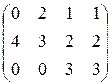 2.
2. 
3.  4.
4. 
5.  6.
6. 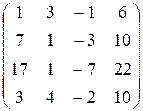
7. 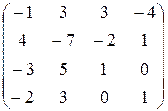 8.
8. 
9.  10.
10. 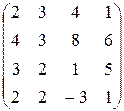
11. 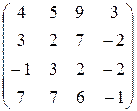 12.
12. 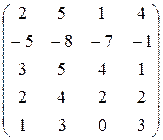
13.  14.
14. 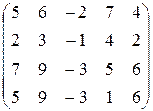
15.  16.
16. 
17. 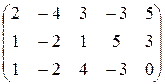 18.
18. 
19.  20.
20. 
21.  22.
22. 
23.  24.
24. 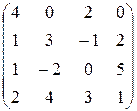
25.  26.
26. 
27.  28.
28. 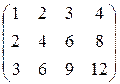
29.  30.
30. 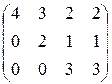
Задание №7
Пример 9. Проверить совместность системы:  .
.
Решение. Расширенная матрица системы имеет вид
 .
.
Переставим первый и третий столбцы  .
.
Прибавим элементы первого столбца, умноженные на 2, к элементам 3 -го и 4 -го столбцов, а из второго вычтем первый столбец:
 .
.
Вычеркнем второй столбец, так как его элементы пропорциональны соответствующим элементам третьего столбца. Элементы третьего столбца умножим на 2 и прибавим к элементам 4 -го:  .
.
Очевидно, что ранг основной матрицы этой системы r (А)= 2, так как минор второго порядка 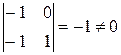 .
.
Ранг расширенной матрицы r (В)=3, так как 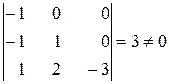 .
.
Таким образом, r (А)=2, r (В)=3, то есть r (А)¹ r (В), поэтому система несовместна.
Пример №10. Исследовать систему уравнений:  .
.
Решение. Преобразуем расширенную матрицу системы с помощью элементарных преобразований:
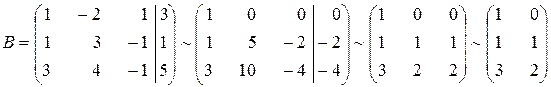 .
.
Очевидно, что r (А)= r (В)=2. По теореме Кронекера-Капелли система совместна.
Запишем первое и второе уравнения заданной системы:

За базисные неизвестные примем х 1 и х 2, так как определитель  из коэффициентов при этих неизвестных отличен от нуля. Свободным неизвестным служит х 3. Переписав систему в виде
из коэффициентов при этих неизвестных отличен от нуля. Свободным неизвестным служит х 3. Переписав систему в виде

выразим х 1 и х 2 через х 3:
 ,
,  .
.
Полагая х 3 = u, получим решение системы в виде
 ,
,  ,
,  .
.
Придавая u различные числовые значения, будем получать различные решения данной системы уравнений.
Примеры для самостоятельной работы
Исследовать систему уравнений:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13. 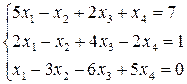 14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 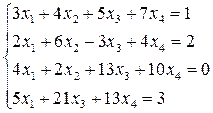
21.  22.
22. 
23.  24.
24. 
25.  26.
26. 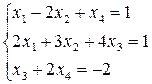
27.  28.
28. 
29.  30.
30. 
Задание № 8
Пример 11. Решить методом Крамера систему уравнений
 .
.
Решение. Вычислим определитель системы
 .
.
Следовательно, система имеет единственное решение. Найдем Dх1, Dх2, Dх3.
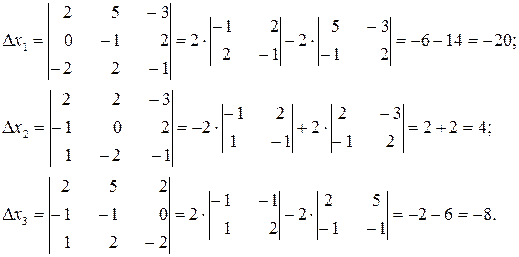
Определим решение системы уравнений по формулам Крамера:







