1) Развёртка боковой поверхности цилиндра является квадратом, диагональ которого равна 10см. Найдите площадь боковой поверхности цилиндра.
2) Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 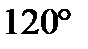 . Высота цилиндра равна 5см, радиус цилиндра -
. Высота цилиндра равна 5см, радиус цилиндра - 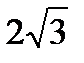 см.
см.
Найдите площадь сечения.
3) Развёртка боковой поверхности цилиндра является прямоугольником, диагональ которого равна 8см, а угол между диагоналями - 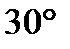 . Найдите площадь боковой поверхности цилиндра.
. Найдите площадь боковой поверхности цилиндра.
4) Сечение цилиндра плоскостью, параллельной его оси, есть квадрат. Эта плоскость отсекает от окружности основания дугу в 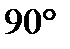 . Радиус цилиндра равен 4см. Найдите площадь сечения.
. Радиус цилиндра равен 4см. Найдите площадь сечения.
РАБОТА № 44
Объём призмы
1) Измерения прямоугольного параллелепипеда 2,5см, 5см и 5см. Найдите ребро куба, объём которого в два раза больше объёма параллелепипеда.
2) Найдите объём прямой призмы АВСА1В1С1, если 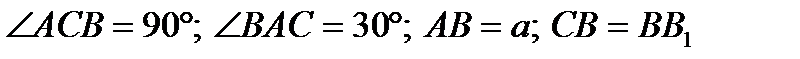 .
.
3) Измерения прямоугольного параллелепипеда 2см, 6см и 6см. Найдите ребро куба, объём которого в три раза больше объёма параллелепипеда.
4) Найдите объём прямой призмы АВСА1В1С1, если 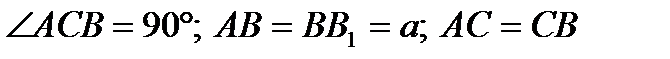 .
.
РАБОТА № 45
Площадь поверхности прямой призмы
Вычисли и заполни таблицу:
| Основание прямой призмы | Высота | Sбок. | Sполн. |
Треугольник АВС, АС=15см, ВС=20см, 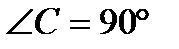
| 12см | ||
Параллелограмм АВСК,АВ=3,АК=4, 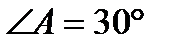
| |||
| Прямоугольник, стороны которого 14см и 5дм. | 9см | ||
Трапеция АВСК,АВ=7см,АК=3см, 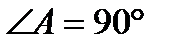 , , 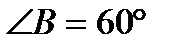
| 8см |
РАБОТА № 46
Правильная пирамида
В n-угольной правильной пирамиде a – сторона основания, к – боковое ребро, h – высота, L– апофема
| n | a | к | h | n | a | h | L | ||
| А) | 12см | 15см | Д) | 18см | 13см | ||||
| Б) | 13дм | 18дм | Е) | m | n | ||||
| В) | m | n | Ж) | 6дм | 6  дм дм
| ||||
| Г) | m | n | З) | m | n |
РАБОТА № 47
Правильные многогранники
Заполни таблицу:
| Тип многогранника | Число граней | Число вершин | Число рёбер |
РАБОТА № 48
Площадь поверхности цилиндра
В цилиндре r – радиус основания, h – высота. Найти х и у и заполнить таблицу.
| r | h | Sбок. | Sцил. | |
| А) | 1см | 2см | ||
| Б) | 2см | 1см | ||
| В) | 25м | 10,5м | ||
| Г) |  см см
| 7см | ||
| Д) | 28см2 | 40см2 | ||
| Е) | х | а | у | 2у |
| Ж) | 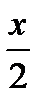
| х | 28см2 | |
| З) | 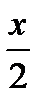
| х | 12  м2 м2
|
РАБОТА № 49
Площадь поверхности конуса
В цилиндре r – радиус основания, h – высота,
l - образующая. Найти х и заполнить таблицу.
| r | h | l | Sбок. | Sкон. | |
| А) | 1см | 2см | |||
| Б) | 12см | 5см | |||
| В) | 3м | 5м | |||
| Г) | х | х | 36 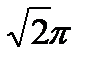 см2 см2
| ||
| Д) | 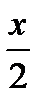
| а | х | ||
| Е) | 27см | 810  см2 см2
|
РАБОТА № 50
Объём прямоугольного параллелепипеда
В прямоугольном параллелепипеде с квадратным основанием р – сторона основания, с - высота. Заполнить таблицу.
| А) | Б) | В) | Г) | Д) | Е) | |
| р | 3 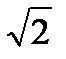
| |||||
| с | 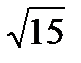
| l | ||||
| V | 1,76 | 122,4 | 12 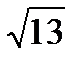
| Q |
РАБОТА № 51
Объём прямоугольного параллелепипеда
Дан прямоугольный параллелепипед, основанием которого является квадрат.
| А) | Б) | В) | Г) | Д) | Е) | |
| Сторона квадрата | 3,5 | |||||
| Диагональ квадрата | 5 
| 2 
| d | |||
| Периметр квадрата | 4 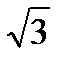
| P | ||||
| Высота паралл-да | 9,8 | c | ||||
| Объём паралл-да | 12,74 | 28,4 | V |
РАБОТА № 52
Уравнение сферы
- Укажите центр и радиус сферы, заданной уравнением
а) (х – 4)2 + (у – 2)2 + (z + 9)2 = 25;
б) (х – 3,6)2 + (у + 0,75)2 + (z + 777)2 = 1,21
- Проверьте, лежит ли точка А на сфере
а)(х + 1)2 + (у – 2)2 + (z – 3)2 = 9,если А(-1;-1;3)
б)(х - 2)2 + (у + 3)2 + (z + 4)2 = 16, если А(4;-3;-2)
- Напишите уравнение сферы радиуса R с центром в начале координат, если
а) R = 8; б)R = 2,5
- Напишите уравнение шара радиуса R с центром в начале координат, если R = 6.
- Напишите уравнение сферы радиуса R с центром в точке С, если С(-3;2;4) и R = 5
- Напишите уравнение шара радиуса R с центром в точке С, если С(5;4;-2) и R = 0,5
- Составьте уравнение сферы с центром в точке С, проходящей через точку М, если
а) С(0;-4;9), М(6;-1;0); б) С(-2;4;0), М(-2;4;3)
- Докажите, что каждое из следующих уравнений задаёт сферу. Найдите координаты центра и радиус этих сфер
а) х2 – 9х + у2 + 2у + z2 = 34;
б) х2 + у2 – 3z + z2 + 5у - х – 18 = 0
9. Найти координаты точек пересечения сферы с координатными осями
(х + 3)2 + у2 + (z - 5)2 = 25
РАБОТА № 53
Объём цилиндра
Пусть r – радиус основания, h – высота, V – объём цилиндра. Заполнить таблицу.
| r | h | V | |
| А) | |||
| Б) | 2 
| ||
| В) | 0,5 | 9 
| |
| Г) | 6,4 
| ||
| Д) | 3,6 | ||
| Е) | 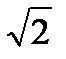
| 3 
|
РАБОТА № 54
Объём наклонной призмы
Вычисли объем фигуры:
| Основание | Высота | Объём | |
| А) | Треугольник АВС, АВ=ВС=СА=3см | 15см | |
| Б) | Треугольник АВС, АВ=5м, ВС=6м, СА=9м | 20м | |
| В) | Квадрат АВСК, АВ=12 | 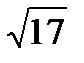
| |
| Г) | Параллелограмм АВСК, АВ=3см, АК=5см, 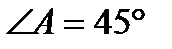
| 8см |
РАБОТА № 55
Объём конуса.
Пусть r – радиус основания, h – высота, V – объём конуса. Заполнить таблицу.
| А) | Б) | В) | Г) | Д) | Е) | |
| h | 3cм | 10м | 2,5м | m | ||
| r | 1,5см | 1,5м | А | |||
| V | 94,2м3 | 48 
| р | Р |
РАБОТА № 56






