СБОРНИК ДОМАШНИХ САМОСТОЯТЕЛЬНЫХ РАБОТ
по дисциплине «Математика»
для студентов первого курса
по специальностям СПО
Тюмень 2015
Сборник домашних самостоятельных работ по математике предназначен для студентов первого курса. В пособие включены домашние и контрольные работы по дисциплине «Математика».
Сборник может применяться для организации учебной деятельности студентов очного обучения для домашней самостоятельной работы.
Разработчик: Дедова Н.Н.,преподаватель математики ЧПОУ ТОСПО «Тюменский колледж экономики, управления и права»
Рецензент: Текутьева А.С. преподаватель математики ГАПОУ ТО «ТСИ и ГХ»
| СОГЛАСОВАНО Протокол заседания цикловой комиссии общеобразовательных дисциплин от___.____.2015 №____ Председатель комиссии ________ Л.А. Скоробогатова | СОГЛАСОВАНО Протокол заседания методического совета от___.____.2015 №____ |
© ЧПОУ ТОСПО «Тюменский колледж экономики, управления и права»
РЕЦЕНЗИЯ
на сборник самостоятельных домашних работ
по математике для студентов первого курса
по специальностям СПО
Сборник разработан по учебной дисциплине «Математика» преподавателем Частного профессионального образовательного учреждения Тюменского областного союза потребительских обществ «Тюменский колледж экономики, управления и права» Дедовой Н.Н. в соответствии с требованиями Федерального государственного образовательного стандарта для специальностей среднего профессионального образования. Подготовка специалистов любого профиля предусматривает изучение дисциплин естественнонаучного цикла. Настоящая работа составлена в целях формирования математических умений студентов самостоятельно применять полученные теоретические знания по предмету в рамках, изученных тем, а также способствует формированию знаний в области практического применения науки и развитию творческих способностей студентов.
Сборник состоит из 57 домашних самостоятельных работ и 10 контрольных работ по темам программы. Работы, включенные в практикум, дают возможность преподавателю варьировать их подбор в соответствии с успеваемостью и личными наклонностями студентов. На основании анализа проверочных работ студентов педагог сможет разработать индивидуальный образовательный маршрут. Представленные в сборнике задания позволяют организовать индивидуальную и подгрупповую работу в различных условиях обучения: дифференцированного - развивающего, интегрированного, надомного. При этом содержание адаптировано с учетом индивидуальных особенностей и уровня интеллектуального развития разных категорий студентов.
Сборник предназначен в помощь студентам для закрепления знаний и формирования профессиональных умений и навыков. Данная работа будет полезна для преподавателей и студентов колледжа и всех тех, кто хочет изучать математику.
Рецензент:
Преподаватель ГАПОУ ТО
«Техникум строительной индустрии
и городского хозяйства» А.С. Текутьева
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ | ||
| 1. | № 1 Степень с действительным показателем. | |
| 2. | № 2 Показательная функция. | |
| 3. | № 3 Показательные уравнения. | |
| 4. | № 4 Показательные неравенства | |
| 5. | № 5 Свойства логарифмов. | |
| 6. | № 6 Логарифмическая функция. | |
| 7. | № 7 Степенная функция. | |
| 8. | № 8 Логарифмические уравнения. | |
| № 9 Логарифмические неравенства. | ||
| 10. | № 10 Иррациональные уравнения. | |
| 11. | № 11 Иррациональные неравенства. | |
| 12. | № 12 Системы уравнений. | |
| 13. | № 13 Тригонометрические преобразования. | |
| 14. | № 14 Тригонометрические уравнения. | |
| 15. | № 15 Тригонометрические уравнения. | |
| 16. | № 16 Тригонометрические неравенства. | |
| 17. | № 17 Наибольшее и наименьшее значения. | |
| 18. | № 18 Производная. | |
| 19. | № 19 Уравнение касательной. | |
| 20. | № 20 Исследование функций. | |
| 21. | № 21 Интеграл. | |
| 22. | № 22 Первообразная. | |
| 23. | № 23 Площадь криволинейной трапеции. | |
| 24. | № 24 Итоговая самостоятельная работа. | |
| 25. | № 25 Основы геометрии. | |
| 26. | № 26 Взаимное расположение прямых в пространстве. | |
| 27. | № 27 Перпендикулярность прямой и плоскости. | |
| 28. | № 28 Перпендикуляр и наклонные. | |
| 29. | № 29 Параллелепипед. | |
| 30. | № 30 Пирамида. | |
| 31. | № 31 Многогранники. | |
| 32. | № 32 Координаты вектора. | |
| 33. | № 33 Скалярное произведение. | |
| 34. | № 34 Объём призмы. | |
| 35. | № 35 Объёмы тел. | |
| 36. | № 36 Взаимное расположение прямых в пространстве | |
| 37. | № 37 Параллельность прямой и плоскости. | |
| 38. | № 38 Перпендикулярность прямой и плоскости. | |
| 39. | № 39 Перпендикуляр и наклонные. | |
| 40. | № 40 Площадь поверхности прямой призмы. | |
| 41. | № 41 Пирамида. | |
| 42. | № 42 Координаты вектора. | |
| 43. | № 43 Площадь поверхности цилиндра. | |
| 44. | № 44 Объём призмы. | |
| 45. | № 45 Площадь поверхности прямой призмы. | |
| 46. | № 46 Правильная пирамида. | |
| 47. | № 47 Правильные многогранники. | |
| 48. | № 48 Площадь поверхности цилиндра. | |
| 49. | № 49 Площадь поверхности конуса. | |
| 50. | № 50 Объём прямоугольного параллелепипеда. | |
| 51. | № 51 Объём прямоугольного параллелепипеда. | |
| 52. | № 52 Уравнение сферы. | |
| 53. | № 53 Объём цилиндра. | |
| 54. | № 54 Объём наклонной призмы. | |
| 55. | № 55 Объём конуса. | |
| 56. | № 56 Площадь поверхности и объём шара. | |
| 57. | № 57 Площадь поверхности и объём тел вращения. | |
| 58. | КОНТРОЛЬНАЯ РАБОТА № 1 Действительные числа. | |
| 59. | КОНТРОЛЬНАЯ РАБОТА № 2 Степенная функция. | |
| 60. | КОНТРОЛЬНАЯ РАБОТА № 3 Показательная функция. | |
| 61. | КОНТРОЛЬНАЯ РАБОТА № 4 Логарифмическая функция. | |
| 62. | КОНТРОЛЬНАЯ РАБОТА № 5 Тригонометрические формулы. | |
| КОНТРОЛЬНАЯ РАБОТА № 6 Тригонометрические уравнения. | ||
| 64. | КОНТРОЛЬНАЯ РАБОТА № 7 Тригонометрические функции. | |
| 65. | КОНТРОЛЬНАЯ РАБОТА № 8 Производная. | |
| 66. | КОНТРОЛЬНАЯ РАБОТА № 9 Производная. | |
| 67. | КОНТРОЛЬНАЯ РАБОТА № 10 Первообразная. | |
| 68. | Литература |
ВВЕДЕНИЕ
Важнейшим направлением повышения качества обучения является совершенствование домашней самостоятельной познавательной деятельности студентов. В сборник домашних работ по математике включены домашние и практические работы, содержащие творческие, нестандартные задачи по каждой изучаемой теме, а также задачи повышенной сложности. Эти задания в полном объеме или частично предлагаются студентам в качестве зачетных, а также используются как дополнительные задания для проведения контрольных работ.
Задания, представленные в данном сборнике, можно использовать при подготовке к сдаче экзаменов.
При решении задач на вычисление следует, если это возможно, применять формулы сокращённого умножения, группировку, вынесение общего множителя за скобку и др. При решении уравнений и неравенств, и их систем следует чаще применять свойства функций: монотонность, ограниченность, чётность. При решении уравнений и неравенств, содержащих модуль, применять их свойства. При решении иррациональных, показательных, логарифмических и комбинированных неравенств - применять метод замены множителей. При решении геометрических задач следует использовать формулы нахождения объёмов и площадей для различных геометрических фигур.
РАБОТА № 1
Степень с действительным показателем
1) Найдите значение выражения
1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  7)
7)  8)
8) 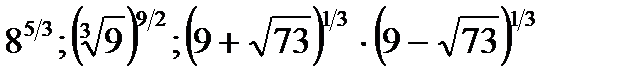 9)
9) 
|
2) Сравните числа
1)  2)
2)  3)
3)  4)
4) 
|
| 3) Дана функция f(x) = ax. Известно, что f(– 1,5) = 8. Найдите f(0,5). 4) Дана функция f(x) = ax. Известно, что f(1,5) = 1/8. Найдите f(– 2). |
4) Упростите выражение
1)  2)
2)  3)
3)  4)
4) 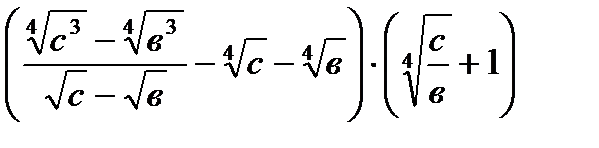 5)
5)  6)
6) 
|
РАБОТА № 2
Показательная функция
1) Изобразите схематически график и опишите свойства функции
а) у =  б) у =
б) у = 
|
2) Постройте график функции у = 2х – 1 (у = 3х – 1); назовите множество значений функции; выделите на рисунке часть графика, для которой
– 1/2 < y < 3 (– 2/3 < y < 2), и найдите соответствующие значения х.
3) Решите графически уравнение
| а) (1/2)х = 2 – х б) 3х = 2х + 3) |
4) Решите графически неравенство
| а) 3х < 1/3 б) (1/2)х > 2 |
РАБОТА № 3
Показательные уравнения
1. Решите уравнения
1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  7)
7) 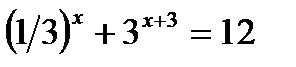 8)
8)  9)
9) 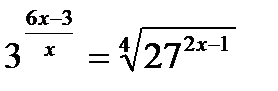 10)
10)  11)
11) 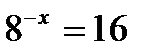 12)
12)  13)
13)  14)
14)  15)
15) 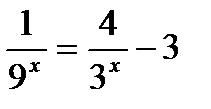 16)
16)  17)
17)  18)
18)  19)
19)  20)
20) 
|
РАБОТА № 4
Показательные неравенства
1. Решите неравенства
1)  2)
2) 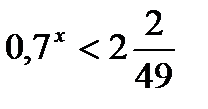 3)
3)  4)
4)  5)
5)  6)
6)  7)
7)  8)
8)  9)
9)  10)
10)  11)
11)  12)
12)  13)
13)  14)
14) 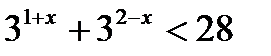 15)
15)  16)
16) 
|
РАБОТА № 5
Cвойства логарифмов
1) Вычислить


|
2) Найти область определения функции
 3)
3)

 6)
6) 
|
3) Прологарифмируйте по основанию 10 выражение:
1) х =  2) х =
2) х = 
|
3) Найдите х, если
1)  2)
2) 
|
4) Вычислите
а) log2535, если log57 = p
б)  , если , если 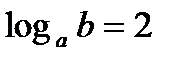 в) log4921, если log73 = c
г)
в) log4921, если log73 = c
г)  , если , если 
|
РАБОТА № 6
Логарифмическая функция
1) Изобразите схематически график и опишите свойства функции
а) у = log 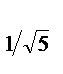 x
б) у = log x
б) у = log  x x
|
2) Постройте график функции у = log2x – 1 (у = log2(x – 1)); назовите множество значений функции; выделите на рисунке часть графика, для которой – 2 < y < 1
(– 1< y < 2), и найдите соответствующие значения х.
РАБОТА № 7
Степенная функция
1) Изобразите схематически графики функций
а) у = х  ,(х > 0);
б) у = ,(х > 0);
б) у =  с) у = х
с) у = х 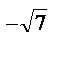 ,(х > 0);
д) у = (х – 1)п + 1,5, (х > 1)) ,(х > 0);
д) у = (х – 1)п + 1,5, (х > 1))
|
2) Возрастает или убывает функция у = х р, (х > 0), если
а) р =  ; р = lg17
б) p = ; р = lg17
б) p =  ; p = ; p = 
|
3) Решите графически уравнения
а)  ;
б) ;
б)  в)
в)  ;
г) ;
г) 
|
Найдите наибольшее значение этой функции на отрезке [0,5;8] ([1,5;9]).
4) Решите графически уравнение
| 1) log3x = 2x – 3 2) log1/2x = – 0,5x + 1) |
5) Решите графически неравенство
| 1)log1/2x > – 3 2) log3x < 2) |
РАБОТА № 8
Логарифмические уравнения
1) Решите уравнения:
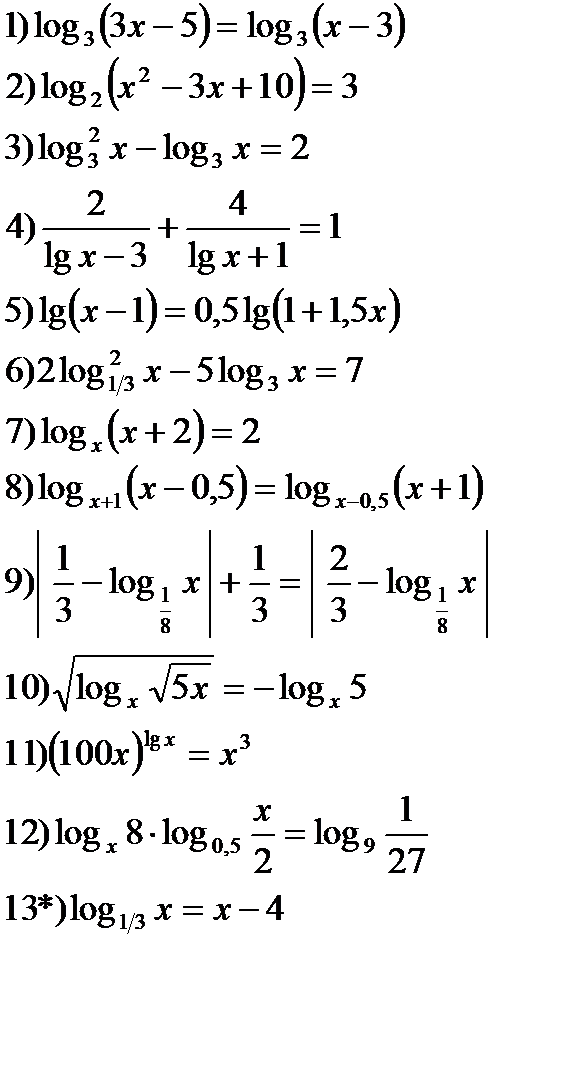

|
РАБОТА № 9
Логарифмические неравенства
1) Решите неравенства
1) log5(2x + 3) > log5(x – 1)
2) log1/2(2x – 5) < – 2
3) lg2x + 3lgx < 4
4) 4x-1 > 7
5) 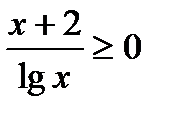 6) lg2x2 + 3lgx > 1
7)
6) lg2x2 + 3lgx > 1
7)  8*)
8*)  – x lgx > 0
9*) – x lgx > 0
9*)  10) log2x+1(3 – 2x) < 1
11) log
10) log2x+1(3 – 2x) < 1
11) log  0,8 < 0
12) 2log5x – logx5 > 1
13) log3log1/2(2x + 1) > 0
14) 0,8 < 0
12) 2log5x – logx5 > 1
13) log3log1/2(2x + 1) > 0
14)  15) (x + 1)log0,73 – log0,727 > 0
16) log3(1 – x) < log3(3 – 2x)
17) log1/2(2x + 5) > – 3
18) lg2x + 5lgx + 6 > 0
19) (3х – 1)(3х – 2)
15) (x + 1)log0,73 – log0,727 > 0
16) log3(1 – x) < log3(3 – 2x)
17) log1/2(2x + 5) > – 3
18) lg2x + 5lgx + 6 > 0
19) (3х – 1)(3х – 2)  0
20) 0
20)  21) 3log
21) 3log  x – 2log2x x – 2log2x  5
22) 5
22)  22*)
22*)  23*) logx2x
23*) logx2x   24) logx-2(2x – 7) < 1
25) log
24) logx-2(2x – 7) < 1
25) log  0,2 > 0
26) 3log7x – 2logx7 < 0
27) log2log 0,2 > 0
26) 3log7x – 2logx7 < 0
27) log2log  (x – 1) < 1
28) (x – 1) < 1
28) 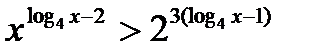 29) (5x – 2)log1,22 – 18log1,22 < 0
29) (5x – 2)log1,22 – 18log1,22 < 0
|
2) При каком значении р решением неравенства является промежуток?
| а) log2(p – 3x) > log2(x2 – 3x); (– 3; 0) б) log3(x2 + 2x) < log3(2x + p); (0; 2) |
3) Найди область определения функции:

РАБОТА № 10
Иррациональные уравнения
1)Решите уравнения
1)  2)
2)  3)
3)  4)
4)  5)
5)  6*)
6*)  7*)
7*)  8)
8)  9)
9)  10)
10)  11)
11)  12)
12)  13)
13)  14)
14)  15)
15)  16)
16)  17*)
17*) 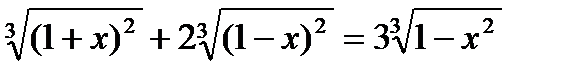 18*)
18*)  19)
19)  20)
20)  21)
21)  22)
22) 
|
РАБОТА № 11
Иррациональные неравенства
1)Решите неравенства
1)  2)
2)  3)
3)  4)
4)  5)
5) 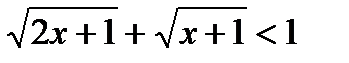 6)
6)  7)
7)  8)
8) 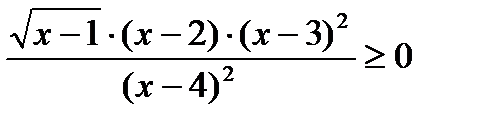 9*)
9*)  10*)
10*)  11*)
11*) 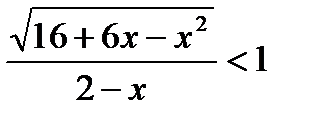 12)
12)  13)
13)  14)
14)  15)
15)  16)
16)  17)
17) 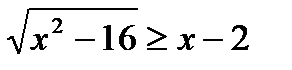 18)
18) 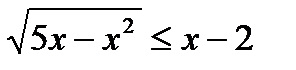 19)
19)  20*)
20*)  21*)
21*)  22*)
22*) 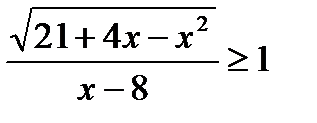
|
2) При каких значениях р решением неравенства является промежуток?
а)  ; [2; 18)
б) ; [2; 18)
б)  ; [– 1; 15) ; [– 1; 15)
|
РАБОТА № 12
Системы уравнений
1) Решите системы уравнений


РАБОТА № 13
Тригонометрические преобразования
1) Вычислить
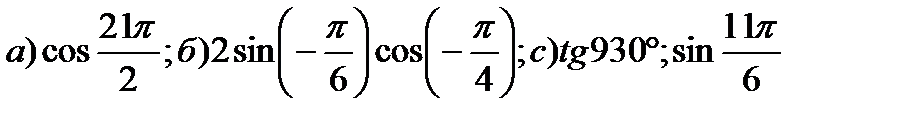
 з)
з)  , если tgx = – 2
и) , если tgx = – 2
и)  , если tgx = – 3 , если tgx = – 3
|
2) Решите уравнения
а) cos(– 3x) = – 1;
б) tg(5п + х) = 0
в) sin(2x + 6п) + cosп/4 = 
|
| г) sin(– 2x) = – 1; д) ctg(7п + х) = 0 е) cos(8п + 3х) + 1 = tgп/4 |
3) Упростите выражения
а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 
|
| 4) Вычислить: а) Дано cosp = – 5/13, п/2 < p < п Найти sin(п/3 – р) б) Дано sinp = 8/17, п/2 < p < п Найти cos(п/6 – р) |
5) Сравните с 0 выражения
| а)cos5; б)tg1,6п; в)sin11п/9 г) sin4; д)cos1,8п; е)ctg9п/7 |
6) Найти х, если
а)  б)
б) 
|
РАБОТА № 14
Тригонометрические уравнения
1)Решите уравнения
1) sinx = 0
2) 2tg3x = 0
3) – 2cosx = 1
4) 2sin(2x – 4п) =  5) sinx cos2x + cosx sin2x = 1
6) 2sinx/2 cosx/2 = – 1
7) cos22x = 2
8) 1 – sin2x = 0
9) 3sin22x + 7cos2x – 3 = 0
10) 2tg43x – 3tg23x + 1 = 0
11) (1 – cos2x)(сtgx +
5) sinx cos2x + cosx sin2x = 1
6) 2sinx/2 cosx/2 = – 1
7) cos22x = 2
8) 1 – sin2x = 0
9) 3sin22x + 7cos2x – 3 = 0
10) 2tg43x – 3tg23x + 1 = 0
11) (1 – cos2x)(сtgx +  ) = 0
12) sinx = sin3
13) tg2x = ) = 0
12) sinx = sin3
13) tg2x =  , на отрезке [– п/2;п]
14) 2cos2x – sinx – 1 = 0; 8 < x < 40
15) cosx = 0
16) 3ctgx = 0
17) – 2sinx = , на отрезке [– п/2;п]
14) 2cos2x – sinx – 1 = 0; 8 < x < 40
15) cosx = 0
16) 3ctgx = 0
17) – 2sinx =  18) 2cos(2x – 4п) =
18) 2cos(2x – 4п) =  19) cosx cos3x – sinx sin3x = 1
20) cos22x – sin22x = – 1
21) 1/2 sin4x = 1
22) 1 – cos2x = 0
23) 2cos23x + 5sin3x – 4 = 0
24) 2tgx – 2ctgx = 3
25) (sinx + 1)(ctg2x –
19) cosx cos3x – sinx sin3x = 1
20) cos22x – sin22x = – 1
21) 1/2 sin4x = 1
22) 1 – cos2x = 0
23) 2cos23x + 5sin3x – 4 = 0
24) 2tgx – 2ctgx = 3
25) (sinx + 1)(ctg2x –  ) = 0
26) cosx = cos4
27) tgx/2= ) = 0
26) cosx = cos4
27) tgx/2=  , на отрезке [– 3п/2;2п]
28) cos2x = 1 – 3cosx; 1 < x < 50 , на отрезке [– 3п/2;2п]
28) cos2x = 1 – 3cosx; 1 < x < 50
|
РАБОТА № 15
Тригонометрические уравнения
1)Решите уравнения
1) сos2x – 5sinx – 3 = 0
2) tgx + ctgx = 2
3) sinx + sin5x = 0
4) 3 – 4cos2x = 0
5) sinx – 7cosx = 0
6) 3sin2x + sinx cosx = 2cos2x
7) 3sin2x –  sin2x + 5cos2x = 2
8) tg2x = sin2x + 5cos2x = 2
8) tg2x =  9) 1 – 2sin
9) 1 – 2sin  = cos = cos  10) sin2x = sin5x
11) cos3x = sinx
12) cosx + cos2x + cos3x + cos4x = 0
13) sin2x sin6x = cosx cos3x
14)
10) sin2x = sin5x
11) cos3x = sinx
12) cosx + cos2x + cos3x + cos4x = 0
13) sin2x sin6x = cosx cos3x
14)  sin2x – sin2x –  cos2x = 1
15) sin22x + sin23x + sin24x + sin25x = 2
16) cos2x – sin2x = 3,5
17) 4sinx + 5cosx = 6
18) sinx + cosx = 2,5 + 5sinx cosx
19) cos2x = 1
15) sin22x + sin23x + sin24x + sin25x = 2
16) cos2x – sin2x = 3,5
17) 4sinx + 5cosx = 6
18) sinx + cosx = 2,5 + 5sinx cosx
19)  = sinx + 2cosx
20) = sinx + 2cosx
20) 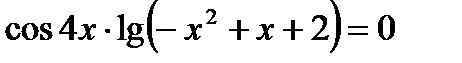 21)
21)  22) (sinx +
22) (sinx +  cosx)sin4x = 2
23) cosx)sin4x = 2
23)  24) cos2x + 3sinx = 2
25) tgx + ctgx = – 2
26) cosx + cos5x = 0
27) 1 – 4sin2x = 0
28)5sinx + 6cosx = 0
29)4sin2x = 3sinx cosx + cos2x
30)2sin2x –
24) cos2x + 3sinx = 2
25) tgx + ctgx = – 2
26) cosx + cos5x = 0
27) 1 – 4sin2x = 0
28)5sinx + 6cosx = 0
29)4sin2x = 3sinx cosx + cos2x
30)2sin2x –  sin2x = – 1
31)ctg2x = sin2x = – 1
31)ctg2x =  32)2cos
32)2cos  – 1 = cos – 1 = cos  33)cos4x = cos6x
34) sin3x = cosx
35) sinx – sin3x – sin5x + sin7x = 0
36) cos3x cos6x = cos4x cos7x
37) sin3x +
33)cos4x = cos6x
34) sin3x = cosx
35) sinx – sin3x – sin5x + sin7x = 0
36) cos3x cos6x = cos4x cos7x
37) sin3x +  cos3x = cos3x =  38)cos2x + cos22x + cos23x + cos24x = 2
39) sin4x + cos4x = 2,5
40) 3sinx + 5cosx = 4
41) sinx – cosx + 5sinx cosx = 1
42)
38)cos2x + cos22x + cos23x + cos24x = 2
39) sin4x + cos4x = 2,5
40) 3sinx + 5cosx = 4
41) sinx – cosx + 5sinx cosx = 1
42)  = cosx – 2sinx
43) = cosx – 2sinx
43)  44)
44) 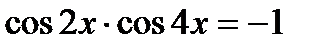 48)
48)  (sinx + cosx) = tgx + ctgx
49) 2sin7x + (sinx + cosx) = tgx + ctgx
49) 2sin7x +  cos3x + sin3x = 0 cos3x + sin3x = 0
|
РАБОТА № 16
Тригонометрические неравенства
1)Решите неравенства
1) sinx < 1/2
2) cos2x > 0
3) tg(2x – п/3)<  4) sinx > cosx
5) 3 – 4cos2x > 0
6)
4) sinx > cosx
5) 3 – 4cos2x > 0
6)  7) cos2x+5cosx+3
7) cos2x+5cosx+3  0
8) cosx > – 1/2
9) sin3x < 0
10) tg(2x + п/6)> 0
8) cosx > – 1/2
9) sin3x < 0
10) tg(2x + п/6)>  11) sinx < cosx
12) 1 – 4sin2 x < 0
13)
11) sinx < cosx
12) 1 – 4sin2 x < 0
13)  14) 2sin2x+3sinx–2
14) 2sin2x+3sinx–2  0
15) logcosxsin2x 0
15) logcosxsin2x  0
17) 2tg2x 0
17) 2tg2x  3tgx
18) 3tgx
18)  19) cosx – sinx – cos2x > 0
20)
19) cosx – sinx – cos2x > 0
20)  21)
21)  22) logxcos2x > 0
22) logxcos2x > 0
|
РАБОТА № 17
Наибольшее и наименьшее значения
1) Найдите наибольшее и наименьшее значение функции на отрезке.
а) f(x) = x3 – 2x2 + x – 3, [1/2; 2]
б) f(x) = 1/2 sin3x, [4п/9; п]
в) f(x) =  , [– 1; 2]
г) f(x) = , [– 1; 2]
г) f(x) =  , [– 1; 2]
д) f(x) = , [– 1; 2]
д) f(x) = 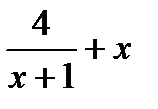 , [0; 3]
е) f(x) = x3 + 3x2 – 9x – 1, [– 4; – 1/3]
ж) f(x) = 1/3 сos2x, [п/6; п]
з) f(x) = , [0; 3]
е) f(x) = x3 + 3x2 – 9x – 1, [– 4; – 1/3]
ж) f(x) = 1/3 сos2x, [п/6; п]
з) f(x) =  , [1/e; e3]
и) f(x) = , [1/e; e3]
и) f(x) =  , [– 1; 2]
к) f(x) = , [– 1; 2]
к) f(x) =  , [– 2; 0] , [– 2; 0]
|
2) При каком значении х функция у = х3 – х2
[ у = х4 + х3] на отрезке [0,5; 1]
([– 1; – 0,5]) принимает наименьшее значение?
3) Найдите область значений функции.
1) f(x) = 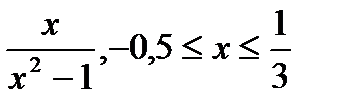 ;
;
2) f(x) =  ;
;
3) Доказать: 
4) Hаибольшее значение функции f(x) = – x2 + bx + c равно 7, а значение с на 25% меньше b. Найти положительное значение b.
5) Hаименьшее значение функции f(x) = x2 + bx + c равно 1, а значение с на 25% больше b. Найти положительное значение b.
6) Найдите наименьшее [ наибольшее ] значение функции на промежутке
| а) f(x) = 3х4 – 8x3 + 6x2 + 5, (– 2; 1) б) f(x) = 4х5 – 15х4 – 3, (– 1; 1) |
7) В каких пределах изменяются значения функции?
а) f(x) = cosx + 1/2 cos2x, x  [0; п]
б) f(x) = sinx + 1/2 sin2x, x [0; п]
б) f(x) = sinx + 1/2 sin2x, x  [– п/2; п/3] [– п/2; п/3]
|
8) Площадь прямоугольника равна 81 см2 [ 25 см2 ]. Найдите наименьший возможный периметр этого прямоугольника.
9) Периметр равнобедренного треугольника равен 20 см [60 см]. При каком значении боковой стороны [ высоты, проведённой к основанию ], площадь треугольника наибольшая?
10) Число 24 [ 18 ] представьте в виде суммы двух положительных слагаемых, таких, что
произведение их квадратов принимает наибольшее значение.
[ сумма их квадратов принимает наименьшее значение. ]
11) Требуется изготовить закрытый [ открытый ] цилиндрический бак ёмкостью V. При каком радиусе основания на изготовление бака уйдёт наименьшее количество материала?
РАБОТА № 18
Производная
1) Найти производные функций
1) f(x) = 5x3 – 3x9
2) f(x) = 6  3) f(x) =
3) f(x) =  4) f(x) = 1/6 х3 – 0,5х2 – 3х + 2
4) f(x) =
4) f(x) = 1/6 х3 – 0,5х2 – 3х + 2
4) f(x) =  5) f(x) =
5) f(x) =  6) f(x) = е – 5х
7) f(x) =
6) f(x) = е – 5х
7) f(x) =  8) f(x) = ln(2x + 1)
9) f(x) = ln cos
8) f(x) = ln(2x + 1)
9) f(x) = ln cos  10) f(x) = log3(2x2 – 3x + 1)
11) f(x) = cos(5 – 3x)
12) f(x) = ctg(2 – 5x)
13) f(x) = 2sin3x cos3x
14) f(x) = log
10) f(x) = log3(2x2 – 3x + 1)
11) f(x) = cos(5 – 3x)
12) f(x) = ctg(2 – 5x)
13) f(x) = 2sin3x cos3x
14) f(x) = log  (x2 – sinx)
15) f(x) = 2x7 + 3x3
16) f(x) = 6 (x2 – sinx)
15) f(x) = 2x7 + 3x3
16) f(x) = 6  17) f(x) =
17) f(x) =  18) f(x) = – 1/6 х3 +1,5х2 +5х – 3
19) f(x) =
18) f(x) = – 1/6 х3 +1,5х2 +5х – 3
19) f(x) =  20) f(x) =
20) f(x) =  21) f(x) = е – 0,3х
22) f(x) =
21) f(x) = е – 0,3х
22) f(x) =  23) f(x) = ln(3x – 4)
24) f(x) = ln sin
23) f(x) = ln(3x – 4)
24) f(x) = ln sin 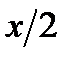 25) f(x) = log1/2(3x2 – 2x + 50)
26) f(x) = sin(3 – 2x)
27) f(x) = tg(4 – 3x)
28) f(x) = cos24x – sin24x
29) f(x) = log
25) f(x) = log1/2(3x2 – 2x + 50)
26) f(x) = sin(3 – 2x)
27) f(x) = tg(4 – 3x)
28) f(x) = cos24x – sin24x
29) f(x) = log  (x2 + cosx) (x2 + cosx)
|
2) Найти значение выражения
а) f '(0,5), если f(x) =  б) f '(– п/4), если f(x) = 3sin2x
в) f '(1) + f(1), если f(x) =
б) f '(– п/4), если f(x) = 3sin2x
в) f '(1) + f(1), если f(x) =  г)f '(–3), если f(x) = e –1/3x –1 + ln(3 – 3x)
д) f '(0) + f '
г)f '(–3), если f(x) = e –1/3x –1 + ln(3 – 3x)
д) f '(0) + f '  ,f(x) = (x2 – 3х)cos3x
е) f '(– 0,5), если f(x) = ,f(x) = (x2 – 3х)cos3x
е) f '(– 0,5), если f(x) =  ж) f '(– 3п/4), если f(x) = 5сos2x
з) f '(1) – f(1), если f(x) =
ж) f '(– 3п/4), если f(x) = 5сos2x
з) f '(1) – f(1), если f(x) =  и) f '(– 2), если f(x) = e 0,5x +1 + ln(1 – 2x)
к) f'(0) + f'
и) f '(– 2), если f(x) = e 0,5x +1 + ln(1 – 2x)
к) f'(0) + f' 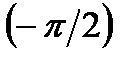 ,f(x) = (3x2 + х)cos2x ,f(x) = (3x2 + х)cos2x
|
3) Решите уравнение у '(х) = 0, если
а) у =  б) у = ln sinx
в) у =
б) у = ln sinx
в) у =  г) у = ln cosx
г) у = ln cosx
|
4) Решите неравенство f '(x) < 0 [ f '(x) > 0 ], если
а)  б)
б) 
|
5) При каких значениях х функция не дифференцируема?
а)  б)
б) 
|
РАБОТА № 19
Уравнение касательной
1)Напишите уравнение касательной к графику функции в точке с абсциссой х0.
| а) f(x) = – x2 – 4x + 2, x0 = – 1 б) f(x) = ln(2x – e), x0 = e в) f(x) = – x2 + 6x + 8, x0 = – 2 г) f(x) = e0,5x, x0 = ln4 |
2) Найдите уравнение касательной к графику функции
| а) f(x) = x2 – 4x + 5 б f (x) = x2 + 3x + 5) |
если эта касательная проходит через точку (0; 4)
[ (0; 1) ] и абсцисса точки касания положительна
[ отрицательна ].
3) К графику функции у = 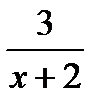 [ у =
[ у =  ] проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой
] проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой
х0 = – 1
[ х0 = 1 ].
Найдите абсциссу точки, в которой другая касательная касается графика данной функции.
4) Какой угол (острый, прямой или тупой) образует с положительным направлением оси Ох касательная к графику функции в точках – 1; 0; 1?
| у = х3 – х2 | у = х2 – х3 |
5) В какой точке касательная к графику функции у = – х2 + 4х – 3 параллельна оси абсцисс?
6) В какой точке касательная к графику функции у = 0,5х2 + 1 параллельна прямой у = – х – 1?
7) Прямая у = х – 2 [ у = – х + 3] касается графика функции у = f(x) в точке х0 = – 1 [ х0 = – 2 ]. Найдите f(– 1) [f(– 2) ].
8) Найдите координаты точки, в которой касательная к графику функции у = log4(x – 2) [ у = log3(5 – x) ] в точке х0 = 3 [ х0 = 4 ] пересекает ось Оу.
9) При каком значении р прямая у = ех + р,
[ у = 2ех + р ] является касательной к графику функции f(x) = lnx?
10) При каком значении р прямая у = 3 + х [ у = 4 – х ] является касательной к графику функции f(x) = e x – p
[ f(x) = e – x – p ]?
11) Найдите уравнение касательной к графику функции 
если эта касательная проходит через точку (– 0,5; 0)
РАБОТА № 20
Исследование функций
1) Найти стационарные (критические) точки функции.
| а) f(x) = – x3/3 + x2/2 + 2x – 3 б f(x) = – x3/3 – x2/4 + 3x – 2) |
2) Найти точки экстремума функции.
а) f(x) = 0,5х4 – 2х3;
б) f(x) = xe  в) f(x) = 1,5х4 + 3х3;
г) f(x) = x(1/e)
в) f(x) = 1,5х4 + 3х3;
г) f(x) = x(1/e) 
|
3) Найти экстремумы функции.
1) f(x) =  2) f(x) =
2) f(x) =  3) f(x) =
3) f(x) =  ; 4) ; 4) 
|
4) Найти промежутки убывания функции.
| 1 f(x) = х3 – 6х2 + 5 2 f(x) = х3 + 9х2 – 4 3) f(x) = lg sinx |
5) Найти промежутки возрастания функции.
6) Найти промежутки возрастания и убывания функции.
1) у =  ;
2)у = 1,5lg2x + lg3x
3) у = ;
2)у = 1,5lg2x + lg3x
3) у =  ;
4)y = (x2 – 2x + 1)x ;
4)y = (x2 – 2x + 1)x  5) у =
5) у = 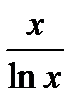
|
7) При каком значении р функция имеет экстремум в точках х1 и х2?
а) f(x) =  , х1 = 2, х2 = – 2
б) f(x) = , х1 = 2, х2 = – 2
б) f(x) =  , х1 = 0, х2 = 6 , х1 = 0, х2 = 6
|
8) Постройте график функции
.
а) у = х3 – 12х + 2
б) у =  в) у = – х4 + 2х3 + 2
г) у = 3х5 – 5х3 + 1
д) у =
в) у = – х4 + 2х3 + 2
г) у = 3х5 – 5х3 + 1
д) у =  е) у = – х3 + 3х + 1
ж) у =
е) у = – х3 + 3х + 1
ж) у =  з) у = х4 – 2х3
и) у = 10х6 – 12х5 – 15х4 + 20х3
к) у =
з) у = х4 – 2х3
и) у = 10х6 – 12х5 – 15х4 + 20х3
к) у =  л) у = cos2x – 2cosx
м) у =
л) у = cos2x – 2cosx
м) у =  н) у = 10
н) у = 10  о) y =
о) y = 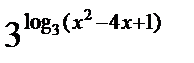 д) у =
д) у = 
|
РАБОТА № 21
Интеграл
1) Вычисли интеграл:

| 
|
2) При каком значении р верно равенство: а) 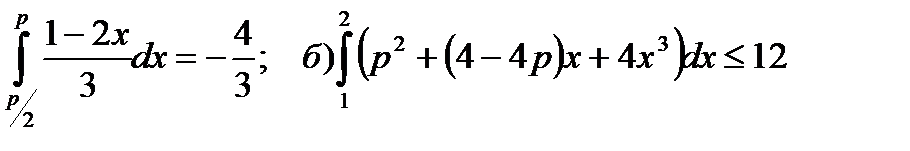
РАБОТА № 22
Первообразная
1) Найти первообразные функций
а) f(x) =  б) f(x) =
б) f(x) =  в) f(x) =
в) f(x) = 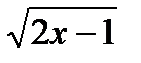 ,
при х > 0,5
г) f(x) = ,
при х > 0,5
г) f(x) =  , если
F(4) = – 2
д) f(x) = , если
F(4) = – 2
д) f(x) =  , если F(1,5) = 1
e) f(x) =( , если F(1,5) = 1
e) f(x) =( ) –1+ ) –1+  , при х > –0,5
ж) f(x) = , при х > –0,5
ж) f(x) =  з) f(x) =
з) f(x) =  и) f(x) = и) f(x) =  к) f(x) =
к) f(x) = 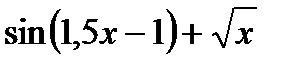 л) f(x) =
л) f(x) = 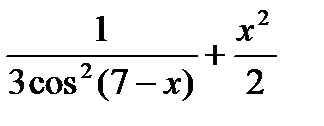 м) f(x) =
м) f(x) = 
| н) f(x) =  о) f(x) =
о) f(x) =  п) f(x) =
п) f(x) =  ,
при х > – 0,5
р) f(x) = ,
при х > – 0,5
р) f(x) =  , если
F(– 15) = 6
с) f(x) = , если
F(– 15) = 6
с) f(x) = 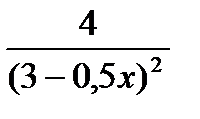 , если F(– 2) = 5
т) f(x) =( , если F(– 2) = 5
т) f(x) =(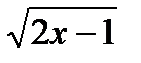 ) –1 – ) –1 –  , при х > 0,5
у) f(x) = , при х > 0,5
у) f(x) =  ф) f(x) =
ф) f(x) =  х) f(x) =
х) f(x) =  ц) f(x) =
ц) f(x) =  щ) f(x) =
щ) f(x) =  ш) f(x) =
ш) f(x) = 
|
2) Для функции f(x) найти первообразную, график которой проходит через данную точку.
1) f(x) = 2sin3x, М(п/3; 0); 2) f(x) = 3сos2x, М(п/4; 0)
3) Найти ту первообразную F(x) функции f(x) = 3х – 1
[f(x) = 2х – 4], для которой уравнение F(x) = 5 [ F(x) = 1 ] имеет 2 равных корня.
4) Найти те первообразную функции f(x) = х2 – 5х + 3 [f(x) = х2 – 2х + 1 ], графики которых касаются прямой
у = – 3х – 1 [у = 4х – 2].
5) В каких точках касательная к у = 1/3х3 – х2 – х + 1 параллельна у = 2х – 1?
РАБОТА № 23
Площадь криволинейной трапеции
1)Вычислите площади фигур, ограниченных графиками
1) у = – х2 + 4х – 3, у = 0
2) у = х2 – 2, у = 2х – 2
3) у = – х2 + х + 2, у = 0
4) у = х2 – 2, у = 2х – 2
5) у = х2 – 2х + 5, х = 0, и касательной в точке х0 = 2
6) у = х2 + 4х + 10, х = 0, и касательной в точке х0 = – 3
7) y = sinx, y = cosx, x = п/4, х = п
8) y = sinx, y = cosx,  9) f(x) = 2x, F(x), если график функции f(x) пересекает график своей первообразной F(x) в двух точках, одна из которых (3; 6).
10) f(x) = – 2x – 4, F(x), x = – 4, если
график функции f(x) является касательной для графика F(x).
11) у =
9) f(x) = 2x, F(x), если график функции f(x) пересекает график своей первообразной F(x) в двух точках, одна из которых (3; 6).
10) f(x) = – 2x – 4, F(x), x = – 4, если
график функции f(x) является касательной для графика F(x).
11) у =  , у = 4 – х
12) у = е -х, у = е, х = е
13) f(x) = 4x, F(x), еслиграфик
функции f(x) пересекает график своей первообразной F(x) в двух точках, одна из которых (– 1; – 4).
14) f(x) = – 2x + 4, F(x), x = 1, если
график функции f(x) является касательной для графика F(x).
15) у = , у = 4 – х
12) у = е -х, у = е, х = е
13) f(x) = 4x, F(x), еслиграфик
функции f(x) пересекает график своей первообразной F(x) в двух точках, одна из которых (– 1; – 4).
14) f(x) = – 2x + 4, F(x), x = 1, если
график функции f(x) является касательной для графика F(x).
15) у =  , у = 6 – х
16) у = ех, у = е2, х = 0 , у = 6 – х
16) у = ех, у = е2, х = 0
|
РАБОТА № 24
Итоговая самостоятельная работа.
1)Найти:
а)sin(arccos4/5);
б)cos(arcsin1/6);
в)cosxcosy, если х=  ,у=
,у= 
г)  ;
;
д) tg  , если
, если  ;
;
е) 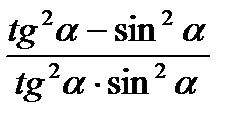
ж) 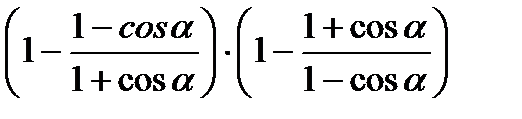 , если tg
, если tg 
з) (1/9) 
и) lg(x3 + 8) – 0,5lg(x2 + 4x + 4) – lg(x2 – 2x + 4)
2) Решить уравнения.
а) arсcos(x – 1) = п/4
б) arctg(4x + 2) = – п/6
в) 
г) 
д) logx – 1(x2 – 5x + 10) = 2
е) 
ж) 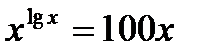
3) Решить неравенства.
а)sinx+  cosx <0;
cosx <0;
б)sin2x  ;в)2cos2x+5cosx– 3<0
;в)2cos2x+5cosx– 3<0
г)5lgx – 3lgx – 1 < 3lgx + 1 – 5lgx – 1;
д)log2(9 – 2x) < 3 – x;
е)2logx25 – 3log25x > 1
4) Найти угловой коэффициент и угол наклона касательной, проведённой к графику функции у = 1 + sinx в точке с абсциссой х0 = п.
РАБОТА № 25
Основы геометрии
1) Найти площадь равнобедренного треугольника с углом  при основании, если
при основании, если
а) боковая сторона равна с;
б) основание равно р
2) Стороны параллелограмма 6 и 10см, а острый угол равен  . Найти S.
. Найти S.
3) Длина тени дерева 10,2м, а длина тени человека ростом 1,7м равна 2,5м. Найти высоту дерева.
4) В треугольнике АВС:  см. Найти СВ.
см. Найти СВ.
РАБОТА № 26
Взаимное расположение прямых в пространстве
1) Даны четыре точки А; В; С; Е, не лежащие в одной плоскости. Могут ли пересекаться прямые АС и ВЕ? Ответ по






