Тема 3. Дифференциальное исчисление функций нескольких переменных

Понятие функции нескольких переменных. Частные производные 1-го и 2-го порядка. Дифференциал функции

3.1. Вычислить:

1) значения F(2,3), F(1,2), F(2,1), F(a,0), F(0,a), если

2) значения F(2,4), F(4,2), F(1,a), если

3.2. Найти области определения функций:

1) 2) 3)

4) 5) 6)

7)

 

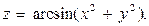
3.3. Построить несколько линий уровня функций:

1) z=xy; 2) z=y-x²; 3) z=

4) z=ln(x²+y²); 5) z=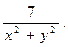

Найти частные производные 1-го порядка функции:

3.4. z=x²-2xy-5y³. 3.5. z=2x³+3x²y-y+5.

3.6. z= e . 3.7. z=ln(x²+y²).

3.8. z= 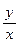. 3.9. z= .

3.10. z= x^y. 3.11. z=x²e^xy.

3.12. z= arctg(). 3.13. z= arcsin .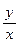

Найти частные производные 2-го порядка:

3.14. z= x²-2xy+5y². 3.15. z= .

3.16. z= . 3.17. z= ln(x²-y²).

3.18. Найти частные производные 3-го порядка для функций:

1) z=2x³+xy²-y³+y²-x; 2) z= .

Производная по направлению и градиент функции

3.19. Найти grad z(x,y) для функции:

1) 2)

3) ; 4)

 

3.20. Построить линии уровня и grad z в точке А(1;2) для функций:

1) z=4-x²-y²; 2) z=x²-y;

3) z=2x+y-3; 4) z= .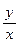

Экстремум функции двух переменных

Найти экстремумы функции:

3.21. z= 3x² +xy+2y²+4x-7y+15.

3.22. z= -x²+2xy-2y² +2x+20.

3.23. z= 5x² +2xy - y²-4x-8y+10.

3.24. z= x³ +8y³ -6xy +1.

3.25. z= 2x³ -xy² +5x²+y².

3.26. z= .

Литература: [1; 2; 6; 7; 9]

Учебно-методическая литература:[5]

Раздел 2. Интегральное исчисление.
Дифференциальные уравнения. Ряды

Тема 4. Интегралы

Понятие неопределенного интеграла.

Нахождение неопределенных интегралов

4.1. Проверить, что:

 

Найти интегралы:

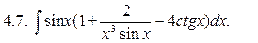
Найти интегралы:

Понятие определенного интеграла. Вычисление определенного интеграла

4.19. Составлением интегральных сумм и переходом к пределу найти интегралы:

4. 20. Вычислить интегральную сумму S₅ для интеграла , разбив отрезок [1;2] на пять равных частей и взяв в каждой части ее середину. Сравнить с точным значением интеграла.

4.21. Выполнить задание предыдущей задачи для интеграла

Вычислить:

4.22. 4.23.

4.24. 4.25.

4.26. 4.27.

Геометрические приложения определенного интеграла

Найти площади фигур, ограниченных линиями:

4.28. у= e^x, х=0, х=1, у=0.

4.29. у= x²+5x+6, х=-1, х=2, у=0.

4.30. у= -x²+2x+3, у=0.

4.31. у=x⁷, х=2, у=0.

4.32. у= ln x, х=e, у=0.

4.33. у= sin x, у=0, .

Найти объемы тел, образованных вращением фигуры, ограниченной линиями:

4.34. у= 4-x², у=0, х=0, где , вокруг: 1) оси Ох; 2) оси Оу.

4.35. у= e^x, x=0, x=1, у=0 вокруг: 1) оси Ох; 2) оси Оу.

4.36. у= x²+1, у=0, х=1, x=2 вокруг: 1) оси Ох; 2) оси Оу.

 

Несобственные интегралы

Исследовать сходимость и вычислить сходящиеся интегралы:

4.37.

4.38. 4.39.

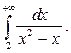4.40. 4.41. 4.42.

 

Литература: [1; 2; 6; 7; 9]

Учебно-методическая литература:[5]

Тема 5. Дифференциальные уравнения

Понятие о дифференциальных уравнениях.

Уравнения 1-го порядка с разделяющимися переменными.

5.1. Выяснить, является ли функция у= решением дифференциального уравнения .

5.2. Выяснить, является ли функция решением дифференциального уравнения

5.3. Является ли функция решением дифференциального уравнения

5.4. Является ли функция решением дифференциального уравнения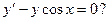

Найти общий интеграл дифференциального уравнения:

5. Линейные дифференциальные уравнения 1-го порядка

Найти общее решение дифференциального уравнения:

Литература: [1; 2; 6; 7; 9]

Учебно-методическая литература: [2; 5]

 

Тема 6. Ряды

Понятие числового ряда. Необходимое условие сходимости ряда.