Понятие функции
1.1. Найти области определения и построить графики функций:
1.2. Найти области определения функций
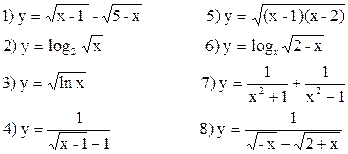
1.3. По заданным функциям 
построить сложную функцию 
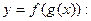
Числовая последовательность и ее предел
1.4. Написать пять первых членов последовательности:
1.5. Написать формулу общего члена последовательности:
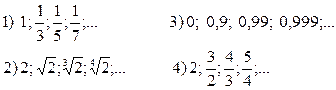
Используя определения предела последовательности, доказать равенства:
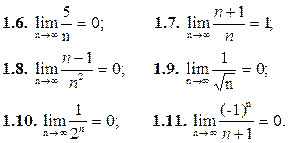
Предел функции
Используя определения предела функции, доказать равенства
Найти пределы:
Используя первый замечательный предел, найти:
Непрерывность функций. Точки разрыва
Найти точки разрыва функции
1.81. Исследовать на непрерывность функцию 
на отрезке:
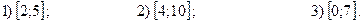
1.82. Исследовать на непрерывность функцию 
на отрезке:
Определить характер точек разрыва:
Литература: [1; 2; 6; 7; 9]
Учебно-методическая литература:[5]
Тема 2. Дифференциальное исчисление функций одной переменной
Понятие производной. Нахождение производных
Исходя из определения производной, найдите производную функции:
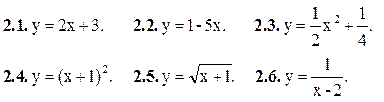
Найти производные:
Пользуясь правилом дифференцирования сложной функции, найти производные функций:
2.9. y=cos (x2 +2x - 4). 2.10. y=sin (x3 - 3x +5).
2.11. y=sin ex. 2.12. y=cos ln x.
2.13. y=e 2x-3. 2.14. y=e 
.
2.15. y=etgx . 2.16. y=esinx.
2.17. y= ln(1+2 
). 2.18. y= ln(2x2 +4x -1).
Составить уравнения касательных к графикам функций:
2.19. y=x2 - 3x + 2 в точке (3;2).
2.20. y= в точке (4;2).
2.21. y= ln x в точке пересечения с осью Оx.
2.22. y= x2 - 5x + 6 в точках пересечения с осью Оx.
2.23. y=e7x в точке пересечения с осью Оy.
Понятие дифференциала.
Производные и дифференциалы высших порядков
Найти дифференциалы функций:
2.24. y= x3 - 3ln x. 2.25. y= cos 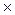x 
ex.
2.26. y= sin 3x. 2.27. y= tg ln x.
2.28. y= x2 arctg x. 2.29. y= 
.
2.30. y=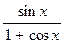 
. 2.31. y= 
.
2.32. Найти приближенно приращение 
у:
1) функции у= 
, если х= 4, х= 0,08;
2) функции у= sinx, если х=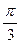 
, х= 0,02;
Найти дифференциалы 2-го порядка от функций:
2.33. y= x3 - 3x2 + x + 1. 2.34. y= (0,1x+1)5.
2.35. y= xcos2x. 2.36. y= sin2x.
Найти производные 3-го порядка от функций:
2.37. y=ex 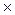cosx. 2.38. y= x2 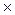ex.
2.39. y=ln(2x+5). 2.40. y= xlnx.
Найти производные n-го порядка от функций:
2.41. y= 
. 2.42. y= e2x.
2.43. y= 5x. 2.44. y= ln(1+x).
Основные теоремы дифференциального исчисления.
Правило Лопиталя
2.45. Удовлетворяют ли условиям теоремы Ролля функции:
1) f(x)=x, x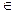 
[0,1];
2) f(x)= 
;
Найти пределы с помощью правила Лопиталя:
2.46. 
2.47. 
2.48. 
2.49. 
2.50. 
2.51. 
2.52. 
2.53. 
2.54. 
2.55. 
Исследование функций и построение графиков.
2.56. Найти максимумы и минимумы и промежутки возрастания и убывания функций:
1) f(x)=x3 - 3x2 - 9x + 5; 2) f(x)=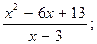 
3) f(x)=xlnx; 4) f(x)= x - arctg2x;
Применение дифференциального исчисления в экономических вопросах.
2.57. Зависимость спроса (объема продаж) от цены выражается формулой d(p)= 
. Определить, для каких p спрос эластичен, неэластичен, нейтрален.
2.58. Зависимость спроса от цены при р 
выражается формулой d(p)= 
, где 
>0-const. Определить, когда спрос будет эластичен, неэластичен, нейтрален.
2.59. Пусть х – объем продаж некоторого товара торговой фирмой, р(х) – функция спроса (выражает зависимость между ценой и объемом продаж), Z(х) – функция издержек (затраты фирмы на реализацию товара). Учитывая, что прибыль от продажи товара находится по формуле V(x) = x p(x) – Z(x), определить:
а) интервалы значений объемов продаж, при которых торговля этим товаром будет прибыльной (убыточной);
б) оптимальные значения объема продаж х* и цены р*, обеспечивающие максимум прибыли V(x), вычислить Vmax.
Используя эскизы графиков функций выручки W(x) =x p(x) и функции издержек Z(x), дать геометрическую интерпретацию полученным результатам.
Выполнить задание для случаев:
1) р(х)=155-3х, Z(x)=1800+5х;
2) р(х)= 100-2х, Z(x)= 375+3х2;
3) р(х)= 
Z(x)=21+х;
Литература: [1; 2; 6; 7; 9]
Учебно-методическая литература: [5]
