Графический способ решения систем логических уравнений.

Рассматривая алгебру высказываний, мы сопоставляем ее с алгеброй чисел. Обратимся к сравнению еще раз. В школьной алгебре для решения уравнений и систем уравнений широко используется графический метод.
В алгебре высказываний графические методы применяются не менее успешно.
При решении логических задач очень часто полезно вычертить “дерево логических условий”. Это “дерево” выражает в виде простого чертежа логическую взаимосвязь между данными высказываниями.
Научимся “выращивать” логические деревья на простых примерах. Выращивание любого дерева начинается с рассмотрения исходной формулы.
Логической сумме на логическом дереве будет соответствовать “разветвление” ветвей.
Логическому произведению на выращиваемом дереве будет соответствовать “следование” ветвей друг за другом.
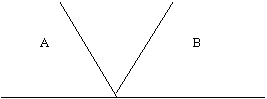
Пример 1. Построить дерево для высказывания А+В.
Решение. Каждому простому высказыванию в формуле на выращиваемом дереве будет соответствовать одна ветвь.

Пример 2.

Пример 3.

Пример 4.

 

Пример 5.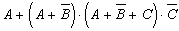

 

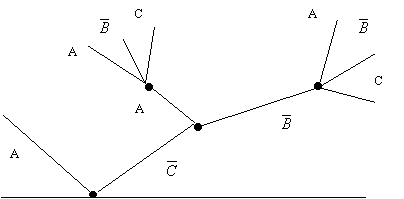
Пример 6.

Пример 7.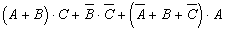

Вернемся к условию задачи № 1, построим к ней графическое дерево и проанализируем каждую его ветвь.
Для вычерчивания графического дерева нам понадобятся уравнения (1), (2), (3).

Проанализируем каждую ветвь.
Ветвь 1:

т.к. T₁× T₂º 0, A₂× T₂º 0
Ветвь 2:

т.к. T₁× T₂º 0
Ветвь 3:

Ветвь 4:
,
т.к. D₃× D₄ º 0
Ветвь 5:
,
т.к. W₂× T₂º 0, T₂× A₂º ₀
Ветвь 6:
,
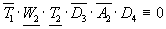т.к. W₂×_{T 2}º ₀
Ветвь 7:
,
т.к. W₂× _{A 2}º ₀
Ветвь 8:
,
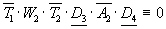т.к. D₃× D₄ º ₀
Итак, только выражение ветви 3 эквивалентно 1:

Из этого выражения следует:
Таня - первая;
Алла - вторая;
Даша - третья;
Валя - четвертая.

Решение логических задач на ЭВМ.

Имея математическую модель для задачи № 1 в виде системы уравнений (1), (2), (3) можно составить алгоритм.

Паскаль-программа.

PROGRAM LOGIKA;
USES CRT;
LABEL 20,30,40,50,60,70;
VAR
T1,W2,T2,D3,A2,D4:INTEGER;
F1,F2,F3,F4,F5,F6,F7,F8,F:INTEGER;
BEGIN
CLRSCR;
T1:=0;
20: W2:=0;
30: T2:=0;
40: D3:=0;
50: A2:=0;
60: D4:=0;
70: F1:=(T1 AND NOT W2) OR (NOT T1 AND W2);
F2:=(T2 AND NOT D3) OR (NOT T2 AND D3);
F3:=(A2 AND NOT D4) OR (NOT A2 AND D4);
F4:=NOT(A2 AND W2);
F5:=NOT(T2 AND A2);
F6:=NOT(T2 AND W2);
F7:=NOT(D3 AND D4);
F8:=NOT(T1 AND T2);
F:=F1 AND F2 AND F3 AND F4 AND F5 AND F6 AND F7 AND F8;
IF F=1 THEN BEGIN WRITELN(' F ',' T1 ','W2 ','T2 ','D3 ','A2 ','D4 ');
WRITELN(F:2,T1:3,W2:3,T2:3,D3:3,A2:3,D4:3); END;
IF D4<1 THEN BEGIN D4:=1; GOTO 70;END;
IF A2<1 THEN BEGIN A2:=1; GOTO 60;END;
IF D3<1 THEN BEGIN D3:=1; GOTO 50;END;
IF T2<1 THEN BEGIN T2:=1; GOTO 40;END;
IF W2<1 THEN BEGIN W2:=1; GOTO 30;END;
IF T1<1 THEN BEGIN T1:=1; GOTO 20;END;
END.

Домашнее задание.
Задача. В спортивных соревнованиях принимали участие пять пионерских команд: "Вымпел", "Метеор", "Нептун", "Старт" и "Чайка". Об их итогах соревнования имеется пять высказываний:
1) Второе место занял "Вымпел", a "Cтарт" оказался на третьем.
2) Хорошо выступала команда "Нептун", она стала победителем, а "Чайка" вышла на второе место.
3) Да нет же, " Чайка" заняла только третье место, а "Нептун"- был последним.
4) Первое место по праву завоевал "Cтарт", а "Метеор" был четвертым.
5) Да, "Метеор" действительно был четвертым, а "Вымпел" был вторым.
Известно, что команды не делили места между собой и что в каждом высказывании одно утверждение правильное, а другое нет.
Как распределились места между командами?

III. Контрольная работа №1 "Истинность высказываний. Тавтологии. Эквивалентности. Законы логики. Тождественные преобразования."

Вариант №1.

1. Докажите эквивалентность:
   
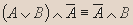
2. Докажите, является ли данное высказывание тавтологией:
   
3. Установите истинность высказывания:
   
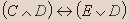
4. Для формулы придумайте формализуемое ею высказывание:
   
5. Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний:
   
6. Упростите:
   

Вариант №2.

1. Докажите эквивалентность:
   
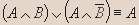
2. Докажите, является ли данное высказывание тавтологией:
   
3. Установите истинность высказывания:
   
4. Для формулы придумайте формализуемое ею высказывание:
   
5. Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний:
   
6. Упростите:
   

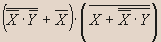
Вариант №3.

1. Докажите эквивалентность:
   
2. Докажите, является ли данное высказывание тавтологией:
   
3. Установите истинность высказывания:
   
4. Для формулы придумайте формализуемое ею высказывание:
   
5. Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний:
   
6. Упростите:
   

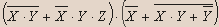
Вариант №4.

1. Докажите эквивалентность:
   
2. Докажите, является ли данное высказывание тавтологией:
   
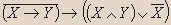
3. Установите истинность высказывания:
   
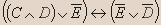
4. Для формулы придумайте формализуемое ею высказывание:
   
5. Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний:
   
6. Упростите: