С помощью таблиц истинности можно установить эквивалентность двух или нескольких высказываний.
Высказывания называются эквивалентными, если соответствующие значения каждого из них совпадают в таблице истинности.
Пример 2. Утверждается, что высказывание А+В· С эквивалентно
высказыванию (А+В)· (А+С)
Решение. Проверка ведется путем составления таблицы истинности.
| А | В | С | В· С | А+В· С | А+В | А+С | (А+В)· (А+С) |
Сравнивая 5-ю и 8-ю колонки убеждаемся, что все значения, получаемые по формуле А+В· С, совпадают со значениями, получаемыми по формуле (А+В)· (А+С), т.е. высказывания эквивалентны (равносильны). Одно может заменить другое.
Эквивалентные (равносильные) высказывания соединяют знаком 
А + В·С  (А+В)· (А+С).
(А+В)· (А+С).
Отметим различие между эквивалентностью и эквиваленцией.
Эквиваленция является логической операцией, позволяющей по двум заданным высказываниям А и В построить новое А  В.
В.
Эквивалентность же является отношением между двумя составными высказываниями, состоящим в том, что их значения истинности всегда одни и те же.
Тавтология.
Пусть дано высказывание А· 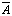 и необходимо составить таблицу истинности.
и необходимо составить таблицу истинности.
| А | 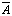
| А· 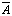
|
Рассмотрим высказывание В+ 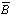 .
.
| В | 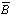
| В+ 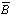
|
Высказывания, истинность которых постоянна и не зависит от истинности входящих в них простых высказываний, а определяется только их структурой, называются тождественными или тавтологиями.
Различают тождественно-истинные и тождественно-ложные высказывания.
В формулах каждое тождественно-истинное высказывание заменяется 1, а тождественно-ложное - 0. Закон исключенного третьего.
A· 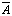
 0
0
В+ 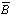
 1
1
Пример 3. Докажите тавтологию (X  Y)
Y)  (X
(X  Y)
Y)
Решение.
| X | Y | X  Y Y
| X  Y Y
| (X  Y) Y)  (X (X  Y) Y)
|
Домашнее задание.
Выучить конспект.
Выполнить примеры:
Пример 1. Докажите тавтологию ((X  Y)
Y)  (Y
(Y  Z))
Z))  (X
(X  Z)
Z)
Пример 2. Установить истинность высказывания. 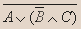
Пример 3. Эквивалентны ли высказывания:  и
и 
СОСТАВЛЕНИЕ ТАБЛИЦ ИСТИННОСТИ.
ЗАКОНЫ ЛОГИКИ.
Наглядность и оборудование: ПК, файл д_з.doc, сам_раб.doc (logika\2\11klass\file\urok5-6\...)., программа Matlog (logika\5\...).
План урока.
- Актуализация опорных знаний.
- Составление таблиц истинности.
- Самостоятельная работа.
- Изучение нового материала.
Ход урока.
I. Актуализация опорных знаний.
A) Беседа.
- Что такое таблица истинности?
- Для чего применяются таблицы истинности?
- Расскажите технологию построения таблиц истинности.
- Что такое эквивалентность?
- Чем отличается эквиваленция от эквивалентности?
- Что такое тавтология?






