Разделение параметров на определяемые и определяющие подразумевает наличие аналитических или обобщенных функциональных зависимостей, отображающих физическое явление или процесс. Эти зависимости вытекают из самой природы рассматриваемого процесса и ни в коем случае не являются придуманными и надуманными. При рассмотрении процессов пищевой технологии можно выделить следующие основные законы: сохранения массы и энергии (уравнения материального баланса и неразрывности потока, уравнения теплового баланса), равновесия системы (принцип Ле-Шателье и правило фаз Гиббса), переноса массы и энергии и принцип движущей силы (кинетические уравнения, базирующиеся в основном на дифференциальных и критериальных уравнениях). Некоторые параметры (например, толщина детали или диаметр вала) определяются из прочностных расчетов. Помимо этого в распоряжении проектировщика имеются геометрические соотношения, связывающие, например, геометрические параметры аппарата с площадью теплообмена и массой отдельной детали и всего аппарата. Могут иметь место и другие зависимости. Принятый критерий оптимизации также связан с определяемыми и определяющими параметрами и представляет собой в математической модели целевую функцию. На полученных таким образом аналитических зависимостях и базируется математическая модель.
Математическую модель необходимо представить в виде сводки формул, записанных в такой последовательности, которая обеспечивает возможность расчета каждого определяемого параметра, зависящего от известных (заданных или вычисленных до этого) численных значений других параметров.
Таким образом, математическая модель – это записанная в математических символах абстракция реального явления, так конструируемая, чтобы анализ ее давал возможность проникнуть в сущность явления. Математическая модель процесса не является его копией, она отражает только самые основные соотношения его характеристик или множество подобных процессов, отбрасывая несущественные или случайные явления. Поэтому наряду с принятыми допущениями по факторам, для математической модели также принимаются допущения. Важно, чтобы допущения, принятые в математической модели, были обоснованными.
При разработке математической модели следует обращать на единицы измерения. Расчеты производятся строго в международной системе единиц СИ. Встречающиеся в справочной литературе формулы и данные в других единицах необходимо сразу переводить в систему СИ.
Допустим, что общее число функциональных зависимостей составляет k, которое меньше n. Тогда можно выразить k определяемых переменных через оставшиеся (n – k) переменные. Причем одним из этих определяемых переменных является критерий оптимизации 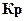 .
.
Таким образом, задача по проектированию аппарата сводится к определению m = (n – k – 1) переменных из условия
Кр(x1, …, xm)→min,
где Кр(x1, …, xm) выступает в качестве целевой функции.
Данная задача относится к задачам математического программирования и решается с помощью специальных методов оптимизации.






