Напомним читателю, что теория массового обслуживания являющаяся одним из важных разделов прикладной математики, в соответствии с интересующими нас вопросами рассматривается как один из аппаратов для анализа и расчетов процессов, связанных с передачей, распределением и обработкой информации вычислительными системами и сетями. Конкретными задачами теории в данном случае является изучение явлений простоев, ожиданий, времени ответа и обслуживания. В связи с этими исходными посылками, применительно к предмету нашего внимани, системой массового обслуживания является любая вычислительная система, в которой поток задач, поступающих в нее, встречает ограничен-
ные ресурсы (например, число процессоров), способные их обработать.
В нашем же учебнике поставлена задача, лишь обратить внимание читателя на то, где можно найти ответы на вопросы, связанные с подробным анализом и описанием этих явлений, сопутствующих процессам функционирования средств вычислительной техники и информационных сетей. С этой целью мы проиллюстрировали некоторые базовые элементы названной теории, общий подход и приемы исследований – «технологию».
10.3.1 Уравнения равновесия
Теория и практика подтвердили, что существуют системы, в которых возможны переходы не только в ближайшие (соседние) состояния, но и в другие, находящиеся «на некотором удалении» от исходного состояния. При исследованиях и расчетах таких систем, как оказалось, также можно использовать свойства марковских цепей. Одним из таких свойств является условие равновесия общего эргодического непрерывного марковского процесса с дискретным множеством состояний.
Основная идея условия равновесия заключается в том, что интенсивность потока вероятностей, входящего в рассматриваемое сосояние, равна интенсивности потока вероятностей, исходящего из этого состояния.
«По-русски», это можно прокомментировать следующим образом. В процессе перехода системы из одного состояния в другое изменяются какие-то характеристики (параметры) системы, которые можно представить некоторым потоком, а сами изменения («мелькания событий») происходят с различными «скоростями» - интенсивностями. Все процессы происходят случайно с различными вероятностями, которые также можно интерпретировать потоком, характеризующимся той же интенсивностью, что и интенсивнось изменения характеристик (параметров).
Математически, в основу этого принципа Марков положил условие:
 (10.16)
(10.16)
где p=[p0, p1, p2, …pk] – вероятности изменений состояний, а Q – матрица интенсивностей потоков между состояниями (интенсивностей переходов).
С учетом дополнительного условия, обозначаемого равенством  , уравнение 10.16 и называют уравнением равновесия системы.
, уравнение 10.16 и называют уравнением равновесия системы.
Интенсивности переходов из рассматриваемого состояния в это же состояние или между двумя различными состояниями определяются по Маркову следующими выражениями:


 ;
;  ,
,
где  - вероятность перехода процесса из состояния
- вероятность перехода процесса из состояния 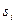 в состояние
в состояние 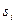 за время
за время  (из рассматриваемого состояния в это же самое состояние) равна
(из рассматриваемого состояния в это же самое состояние) равна  . Аналогично
. Аналогично  - вероятность перехода процесса из состояния
- вероятность перехода процесса из состояния 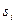 в
в 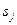 в течение промежутка времени
в течение промежутка времени  равна
равна  . Вы обратили внимание, на то, что величины рассматриваются как бесконечно малые, стремящиеся к нулю? Такие величины называются инфинитезимальными в абстрактномпредставлении «бесконечно малыми». При этом суммарные интенсивности переходов должны удовлетворять условию:
. Вы обратили внимание, на то, что величины рассматриваются как бесконечно малые, стремящиеся к нулю? Такие величины называются инфинитезимальными в абстрактномпредставлении «бесконечно малыми». При этом суммарные интенсивности переходов должны удовлетворять условию:
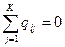 ,
, 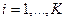 . (10.17)
. (10.17)
Чтобы нагляднее проиллюстрировать содержание условия равновесиия системы, мы воспользовались широко известным примером, имеющим место в многочисленных литературных источниках. В качестве примера в технической литературе рассматривается цепь Маркова с тремя состояниями, приведенная на рисунке 10.8.
На основании такого графа легко составить матрицу интенсивностей переходов:
S1 S2 S3
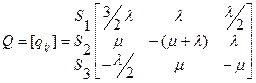 (10.18)
(10.18)

Теоретики считают, что для составления уравнений равновесия, чаще более подходящим является графическое представление системы, чем словесное, математическое или матричное.
По данному графу путем перебора состояний, направлений и интенсивностей перехо-
дов выписываем уравнения, характеризующие динамику системы с учетом того, что в каждом состоянии входящий поток должен равняться исходящему потоку. Получаем систему уравнений:

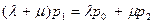 ; (10.19)
; (10.19)
 ,
,
где уравнения (10.18) соответствуют условиям сохранения потока в состояниях  . Последнее уравнение является суммой первых двух. Утверждается, что для цепей Маркова всегда получается точно одно избыточное уравнение. Дополнительным уравнением является нормирующее условие:
. Последнее уравнение является суммой первых двух. Утверждается, что для цепей Маркова всегда получается точно одно избыточное уравнение. Дополнительным уравнением является нормирующее условие:  .
.
Решение системы уравнений имеет вид:
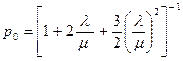 ;
;
 ;
;
 .
.
Таким образом, имеем выражения для вычисления количественных значений вероятностей переходов системы, из одного состояния в другое (не обязательно соседнее) в зависимости от интенсивностей потоков переходов между состояниями для выбранной нами конкретной схемы цепи.
10.3.2 Процессы размножения и гибели
Еще одним подходом при исследованиях поведения различных моделей систем массового обслуживания, к которым относятся и вычислительные системы, широко используется аппарат описания процессов в виде «размножения и гибели». Процесс размножения в вычислительной системе легко связывается с ситуацией последовательного поступления на обработку новых задач (загрузка в память системы новой программы для ее выполнения). Выгрузка только, что законченной программы, - это уход ее из системы – гибель в терминах теории массового обслуживания. При этом рассматривается достаточно многочисленная группа систем. Мы, для знакомства с этим аппаратом исследований, рассмотрим систему общего вида с дискретным пространством состояний и, пред-
ставляющим больший интерес, непрерывным процессом размножения и гибели (по сравнению с дискретным). Поясним, что процесс размножения и гибели был использован как соответствующая модель для описания изменений, происходящих в объеме популяций (каких-то организмов), где отмечалось, что процесс находится в состоянии  , если объем популяции равен
, если объем популяции равен  . Далее переход из состояния
. Далее переход из состояния  в состояние
в состояние  соответствовал рождению (размножению), а переход в
соответствовал рождению (размножению), а переход в  - гибели. Таким образом, рассматривались изменения, переводящие процесс из состояния
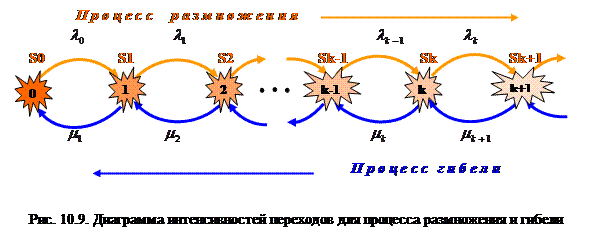
- гибели. Таким образом, рассматривались изменения, переводящие процесс из состояния  только в ближайшие состояния. Для лучшего понимания, обратите внимание на рисунок 10.9 графа интенсивностей переходов для процесса размножения и гибели.
только в ближайшие состояния. Для лучшего понимания, обратите внимание на рисунок 10.9 графа интенсивностей переходов для процесса размножения и гибели.
 |
Процесс характеризуется интенсивностью размножения - 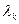 , то есть скоростью, с которой происходит размножение в популяции объема
, то есть скоростью, с которой происходит размножение в популяции объема  и интенсивностью гибели -
и интенсивностью гибели -  , задающей скорость, с которой происходит гибель в популяции объема
, задающей скорость, с которой происходит гибель в популяции объема  . Следует заметить, что интенсивности размножения и гибели не зависят от времени, а зависят только от состояния
. Следует заметить, что интенсивности размножения и гибели не зависят от времени, а зависят только от состояния  .
.
Численные значения 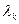 и
и  , принимают соответственно равными:
, принимают соответственно равными: 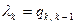 и
и  . Требование о допустимости переходов в ближайшее состояние означает, что популяция должна быть больше 1, то есть
. Требование о допустимости переходов в ближайшее состояние означает, что популяция должна быть больше 1, то есть 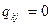 , при
, при 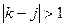 . Более того,
. Более того,  , что означает
, что означает  . При всех вышеперечисленных условиях матрица интенсивностей переходов для общего однородного процесса размножения и гибели принимает вид:
. При всех вышеперечисленных условиях матрица интенсивностей переходов для общего однородного процесса размножения и гибели принимает вид:

Обратите внимание, что главная и соседние с ней диагонали имеют значения, все остальные элементы матрицы равны нулю.
Процесс является процессом размножения и гибели, если он является однородной цепью Маркова с множеством состояний {0, 1, 2, …}, если рождение и гибель являются независимыми событиями и если выполняются следующие условия:
-  , при точно 1-м рождении в промежутке
, при точно 1-м рождении в промежутке 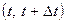 и объеме популяции равном
и объеме популяции равном  ;
;
-  , при точно 1-й гибели в промежутке
, при точно 1-й гибели в промежутке 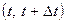 и объеме популяции равном
и объеме популяции равном  ;
;
- 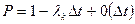 , при отсутствии рождений в промежутке
, при отсутствии рождений в промежутке  в объеме популяции равном
в объеме популяции равном  ;
;
- 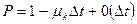 , при отсутствии гибелей в промежутке времени
, при отсутствии гибелей в промежутке времени  в объеме популяции равном
в объеме популяции равном  .
.
Согласно этим условиям кратные рождения, кратные гибели, одновременные рождения и одновременные гибели запрещены.
Задача заключается в определении вероятностей переходов. Не вдаваясь в подробности выкладок, отметим, что в результате некоторых, чисто математических преобразований, получают систему уравнений (уравнения Колмогорова) вида:
 ; (10.19)
; (10.19)
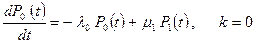 .
.
Решение этой системы представляет собой характеристику 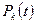 и может быть, например, найдено при условии
и может быть, например, найдено при условии 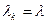 для всех
для всех  и
и  при всех
при всех  , то есть для процесса чистого размножения.
, то есть для процесса чистого размножения.
Решение имеет конечный вид  (10.20)
(10.20)
Это есть ничто иное, как знаменитое распределение Пуассона, занимающее центральное место в теории массового обслуживания.
Граф интенсивностей переходов системы из одного состояния в другое, представленный в виде вытянутой цепочки на рисунке
10.9, является другим способом описания информации, содержащейся в матрице  .
.
В представленной на рисунке 10.9 цепочке состояний некоторой вычислительной системы, каждое из средних состояний (S1, S2, …, Sk-1, Sk, …) связано прямой и обратной стрелкой с каждым из соседних состояний – правым и левым. А крайние состояния (S0,..., Sn) - только с одним соседним состоянием. Такой граф называют графом для схемы гибели и размножения.
Пользуясь таким графом, составим и решим алгебраические уравнения для финальных (конечных) вероятностей состояний:
для первого узла
1) 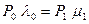 (10.21)
(10.21)
Для второго узла
 ,
,
или
 ,
,
С учетом (10.10) получим для второго узла 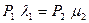 .
.
Из соотношения 1) выразим  через
через 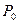 :
:
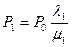 (10.22)
(10.22)
Из соотношения 2) с учетом (10.11) получим
 . (10.23)
. (10.23)
Очевидно, для третьего узла
2) 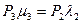 .
.
Рассуждая далее последовательно, по аналогии с предыдущими рассуждениями, можем записать:
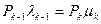 или
или 






