Общим уравнением плоскости называется уравнение
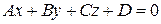, (3.6)
полученное из уравнения плоскости, проходящей через данную точку 
перпендикулярно данному вектору 
:
. (3.7)
Уравнение плоскости, проходящей через три заданные точки: 
, 
, 
имеет вид:
. (3.8)
Каноническими уравнениями прямой в пространстве называют уравнение
. (3.9)
Геометрический смысл канонических уравнений прямой заключаются в том, что они описывают прямую, проходящую через точку параллельно вектору 
, который называется направляющим вектором прямой.
Пример 3.6. Даны координаты вершин A (3;–2;–4), B (–5;3;4), C (1;–3;2), D (4;1;–2) пирамиды ABCD. Найти: а) уравнение прямой АВ, б) уравнение плоскости АВС.
Решение. Найдем координаты векторов 
:
.
а) Для того чтобы найти уравнение прямой AB, воспользуемся формулой прямой, проходящей через две точки:
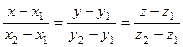. (3.10)
Подставим координаты точек A и B:
, или 
.
б) Для того чтобы найти уравнение плоскости ABC, воспользуемся формулой (3.8). Подставим координаты точек A, B и C:
.
Вычислим этот определитель, разлагая его по первой строке:
Раскрывая скобки и приравнивая нулю полученное выражение, получим уравнение искомой плоскости:
,
или
.
Пример 3.7. Составить канонические уравнения прямой, заданной общими уравнениями:
L: 
Решение. Чтобы составить канонические уравнения прямой, нужно знать какую-либо точку на этой прямой и какой-либо направляющий вектор. Найдем координаты точки. Для этого нужно найти общее решение данной системы двух уравнений, а затем выбрать какое-либо частное решение. Мы поступим несколько иначе, сразу выберем частное решение, для этого придадим какой-либо переменной числовое значение. Тогда останется только две переменные и система станет определенной. Решая полученную систему, найдем числовые значения оставшихся переменных, а, следовательно, и координаты точки на заданной прямой. Пусть x =0, тогда система примет вид:
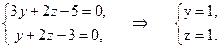
Таким образом, M (0,1,1)Î L. В качестве направляющего вектора прямой можно взять вектор
,
где 
и 
– направляющие векторы плоскостей, входящих в общие уравнения прямой. Так как
={1;3;2}, ={5;1;2},
то
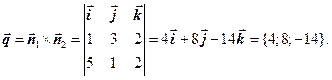
Таким образом,
L: 
Пример 3.8. Найти уравнение плоскости, проходящей через две параллельные прямые:
L 1: 
и L 2: 
.
     L 1 L 2
M 1
M 2
|
Решение. Первая прямая проходит через точку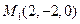 
, вторая через точку 
. Найдем нормальный вектор искомой плоскости:
.
Так как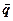 
= {3;2;1}, M 1(2;–2;0), M 2(1;1;1),
={–1;3;1}, то
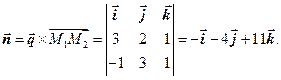
Поскольку M 1Î L, то уравнение искомой плоскости будет иметь вид (см. формулу (3.7)):
P: –1(x– 2)–4(y +2)+11 z =0 Þ P: – x –4 y +11 z– 6=0.
Пример 3.9. Найти координаты точки пересечения плоскости
P:2 x + y–z– 4=0 и прямой L: 
, а также угол между ними.
         L
j
P
|
Решение. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость. Однако гораздо проще определить угол между векторами 
и 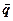. Поскольку
,
то
|cos(
)| = |cos(900 ± j)| = sinj.
Отсюда следует формула для определения угла между плоскостью и прямой:
. (3.11)
В нашем случае
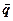= {2;–1;2} и = {2;1;–1}.
Тогда
Þ j» 80.
Чтобы найти точку пересечения L и P, нужно решить систему трех уравнений (одно уравнения дает уравнение плоскости и два уравнения дают уравнения прямой). Однако мы поступим по-другому, представив уравнение прямой в параметрической форме:
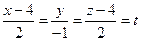Þ 
Подставим выражения для x, y и z в уравнение плоскости и найдем после этого параметр t:
2 x+y–z– 4=0 Þ 2(4+2 t)+(–t) – (4+2 t)–4=0 Þ t =0.
Найдем значения
которые являются координатами точки M пересечения прямой L и плоскости P:
= M (4;0;4).
Кривые второго поряка
Линия – геометрическое понятие, точное и достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах математики различно. В аналитической геометрии линия на плоскости определяется уравнением F (x,y)=0. Если в декартовой системе координат F (x,y) – многочлен какой-либо степени, то линия называется алгебраической, а степень многочлена – порядком линии. В противном случае, линия называется трансцендентной (например, sin x, ln x и др.).
С алгебраической точки зрения наиболее простыми после линий 1-го порядка (прямых) являются линии 2-го порядка, которые в декартовой системе координат в общем виде описываются многочленом второго порядка:
. (3.12)
Наиболее простой линией второго порядка является окружность, каждая точка которой равноудалена от некоторой точки, называемой центром. Чтобы задать окружность, нужно знать координаты ее центра C (x 0, y 0) и ее радиус R. Тогда уравнение окружности можно записать в следующем виде:
. (3.13)
Это есть каноническое уравнение окружности.
Эллипсом называется линия, которая в некоторой прямоугольной декартовой системе координат определяется уравнением
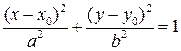(3.14)
при условии a ³ b. Параметры a и b называются большой и малой полуосями эллипса. Точка C (x 0, y 0) – центром эллипса. Точки F 1 и F 2 – это фокусы эллипса, отстоящие от центра на расстояние 
, называемое фокальным расстоянием. Число 
(0 £ e < 1) называется эксцентриситетом эллипса и является мерой его «сплюснутости»
Гиперболой называется линия, которая в некоторой прямоугольной декартовой системе координат определяется уравнением
(3.15)
Параметры a и b называются действительной и мнимой полуосями гиперболы. Точка C(x 0, y 0) – центром гиперболы. Точки F 1 и F 2 – это фокусы гиперболы, отстоящие от центра на расстояние 
, называемое фокальным расстоянием. Уравнения асимптот имеют вид
. (3.16)
Число называется эксцентриситетом, только в случае гиперболы это число e>1. Если a=b, то гипербола называется равносторонней.
Параболой называется линия, которая в некоторой прямоугольной системе координат определяется каноническим уравнением
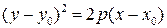. (3.17)
где p >0. Число p называется фокальным параметром параболы, точка C (x 0, y 0) есть вершина параболы, точка F, отстоящая от вершины на расстояние p /2, называется фокусом параболы. Прямая D, перпендикулярная к оси параболы и проходящая на расстоянии p /2 от ее вершины, называется директрисой параболы.
Пример 3.10. Составить уравнение окружности, если известно, что точки A (–7;4) и B (17;–6) являются концами ее диаметра.
Решение. Известно, что центр окружности делит любой диаметр пополам. Поэтому координаты центра окружности находим как координаты точки, делящей отрезок АВ пополам (см. формулу (2.6)):
Радиус окружности будет равен половине диаметра АВ (см. формулу (2.5)):
.
Таким образом, уравнение окружности имеет вид (x –5)2 + (y +1)2 = 132.
Пример 3.11. Вывести уравнение кривой, сумма расстояний от каждой точки которой до двух точек A(–4;0) и B(4;0) есть величина постоянная и равная 10.
Решение. Обозначим через M (x, y) произвольную точку кривой. Запишем геометрическое свойство точек кривой:
| AM | + | BM | = 10.
Распишем это уравнение:
.
Перепишем это уравнение следующим образом:
.
Возведем обе части в квадрат:
,
после упрощений получим
.
Сократив полученное уравнение на 4, возведем его еще раз в квадрат:
.
Раскроем скобки
16 x 2–200 x +625 = 25 x 2–200 x +400+25 y 2 Þ 9 x 2+25 y 2 = 225.
Отсюда получаем
.
Это есть каноническое уравнение эллипса.
Рассмотрим уравнение второго порядка:
.
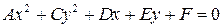Здесь нет смешанного произведения xy. Такое уравнение приводится к каноническому виду при помощи параллельного переноса координат. Аналитически это эквивалентно методу выделения полного квадрата.
Пример 3.12. Показать, что данное уравнение
16 x 2 + 25 y 2 + 32 x – 100 y – 284 = 0
определяет эллипс, приведя его к каноническому виду. Найти центр эллипса, его полуоси и эксцентриситет. Сделать чертеж
Решение. Сгруппируем слагаемые, содержащие x и y:
16(x 2 + 2 x) + 25(y 2– 4 y) – 284 = 0
После этого выражения в скобках преобразуем таким образом, чтобы можно было воспользоваться формулой полного квадрата, т.е. в каждой скобке добавим и отнимем такое число, чтобы можно было воспользоваться формулой: a 2+2 ab + b 2=(a + b)2:
.
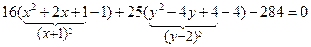Отсюда получаем:
16(x 2+1)2 – 16 + 25(y 2–2)2 – 100 – 284 = 0,
или
16(x 2+1)2 + 25(y 2–2)2 = 400.
Разделив это уравнение на 400, получим
.
Это уравнение – каноническое уравнение эллипса, центр которого находится в точке О (–1,2). Большая полуось равна a =4, малая b =3, фокальное расстояние 
, эксцентриситет e= c / a = 4/5.
Пример 3.13. Показать, что уравнение
9 x 2 –16 y 2 + 18 x + 64 y – 199 = 0
определяет гиперболу, приведя его к каноническому виду. Найти центр гиперболы, ее полуоси, эксцентриситет и уравнения асимптот. Сделать чертеж.
Решение. Дополняя члены, содержащие x и y, до полного квадрата:
9(x 2+2 x) – 16(y 2–4 y) – 199 = 0,
или
9(x +1)2 – 9 – 16(y –2)2 + 64 – 199 = 0.
Отсюда получаем каноническое уравнение гиперболы:
.
Следовательно, центр гиперболы находится в точке С(–1;2), действительная полуось a =4, мнимая b =3, фокальное расстояние 
, эксцентриситет e= c / a = 5/4. Уравнения асимптот имеют вид
,
или 3 x –4 y –10 = 0 и 3 x +4 y –2 = 0.
Построение гиперболы лучше начинать с построения асимптот, а затем уже отмечать вершины, фокусы и другие точки.
Вид уравнения линии зависит не только от вида самой линии, но и от выбора системы координат. Для задания некоторых линий часто используют недекартовы системы координат, поскольку в этих координатах уравнение линии может иметь более простой вид. Большое распространение получила полярная система координат.
Для того чтобы ввести полярную систему координат, нужно задать некоторую точку О, называемую полюсом, и некоторый луч, выходящий из точки О, называемый полярной осью. Тогда любая точка на плоскости однозначно определяется двумя числами (полярными координатами): полярным радиусом r и полярным углом j. Полярный радиус r точки М равен длине радиус-вектора этой точки: 
, а полярный угол j равен углу между радиус-вектором и полярной осью, если полярную ось вращать против часовой стрелки.
Установим теперь взаимосвязь между полярными и декартовыми координатами. Пусть начало прямоугольной декартовой системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Если точка М имеет декартовы координаты x и y и полярные координаты r и j, то, очевидно, что
x = r cosj, y = r sinj, (3.18)
. (3.19)
Уравнение линии в полярной системе координат имеет вид F (r,j)=0 или r= f (j). Для того чтобы соответствие между точками плоскости и полярными координатами было взаимно однозначными, обычно полагают, что r и j изменяются в следующих границах:
0 £ r < +¥, 0 £ j < 2p.
Пример 3.14. Построить кривую, заданную в полярных координатах: r = 4sin3j (трехлепестковую розу).
Решение. Найдем область изменения заданной функции. Поскольку r³0, то и
sin3j ³ 0. Тогда
2p k £ 3j £p+2p k Þ 
.
В результате получаем: при k =0 00£j£600, при k =1 1200£j£1800, при k =2 2400£j£3000. Таким образом, область определения исходной функции состоит из трех секторов. Поскольку все они равноправны, в силу периодичности синуса, то достаточно построить график только в одном секторе.
| j | 100 | 150 | 200 | 300 | 400 | 450 | 500 | 600 | |
| r | 
| 
|
|
|
В итоге получаем следующий график трехлепестковой розы:
ЛИТЕРАТУРА
1. Высшая математика для экономистов. /Под ред. Н.Ш. Кремера. М: ЮНИТИ, 2003.
2. Красс М.С. Математика для экономических специальностей. М: ИНФРА-М, 2001.
3. Гусак А.А. Высшая математика. В 2-х т.: Учеб. пособие. Мн: ТетраСистемс, 2002.
4. Шипачев В.С. Высшая математика. М: Высш. шк., 2003.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М: Высш. шк., 2002.
6. Солодовников А.С., Байбацев В.А., Браилов А.В. Математика в экономике. В 2-х ч. М: Финансы и статистика, 2000.
7. Письменный Д.Т. Конспект лекций по высшей математике. М: Айрис-пресс, 2003.
