Декартовой системой координат называется совокупность точки и базиса. Если базис – ортонормированный, то декартова система называется прямоугольной. Точка в этом случае называется началом координат и обозначается буквой О. Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат. В случае прямоугольной системы координат координатные оси называются, соответственно, абсциссой, ординатой и аппликатой.
Радиус-вектором точки M в заданной системе координат называется вектор 
. Координатами точки М называются координаты ее радиус-вектора и обозначают М (x,y,z).
Рассмотрим две точки A (x 1, y 1, z 1) и B (x 2, y 2, z 2). Координаты вектора 
вычисляются по формуле:
. (2.4)
Расстоянием между двумя точками А и В называется длина вектора 
и обозначается | AB |. Следовательно,
(2.5)
Координаты точки М, делящей отрезок АВ пополам вычисляются по формуле
(2.6)
Пример 2.4. На оси ординат найти точку М, равноудаленную от точек А (1;–4;7) и В (5;6;–5).
Решение. Поскольку точка М лежит на оси Oy, то М (0; y;0). По условию задачи | AM |=| BM |, отсюда
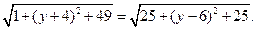
Решая это уравнение, получим y =1. Таким образом, М (0;1;0).
Векторная алгебра
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
. (2.7)
Скалярное произведение векторов обладает следующими свойствами:
10.  ,
| 20.  ,
|
30.  ,
| 40.  .
|
Отметим, что поскольку 
, то для скалярного квадрата используют обозначение 
.
Пример 2.5. Вычислить выражение 
, если 
, 
|, j=2p/3.
Решение. Раскроем скобки, учитывая свойства скалярного произведения векторов:
.
Далее из определения скалярного произведения следует:
18–24–64 = –70.
Тройка векторов называется правой, если вектора, приведенные к одному началу, располагаются также, как расставленные пальцы правой руки: большой палец – по первому вектору, указательный – по второму, средний – по третьему. Если смотреть во внутрь телесного угла, образованного этими векторами, то движение от первого ко второму, от второго к третьему будет совершаться против часовой стрелки. Обычно на практике рассматриваются только правые системы векторов.
| 
|
| Правая тройка | Левая тройка |
Векторным произведением вектора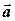 
на вектор 
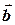называется вектор 
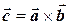, удовлетворяющий следующим условиям:
а) 
,
б) вектор 
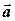перпендикулярен к обоим векторам и ,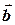
в) упорядоченная тройка 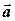, , 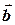– правая.
Векторное произведение векторов обладает следующими свойствами:
10.  ,
| 20.  ,
|
30.  ,
| 40.  .
|
Пример 2.6. Вычислить выражение 
, если 
, 
и j = 2p/3.
Решение. Раскроем скобки внутри модуля, учитывая свойства векторного произведения:
.
Далее, из определения векторного произведения следует:
.
Отметим еще некоторые свойства скалярного и векторного произведений:
Два вектора 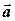и 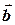перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю: 
.
Два вектора 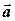и 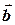коллинеарны тогда и только тогда, когда их векторное произведение равно нулю: 
.
Если два вектора 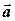и 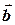определены своими координатами в ортонормированном базисе: 
, 
, то скалярное произведение вычисляется по формуле:
, (2.8)
а векторное произведение по формуле
(2.9)
Геометрический смысл векторного произведения: модуль векторного произведения 
равен площади параллелограмма, построенного на этих векторах, как на сторонах.
Смешанным произведением векторов 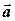, 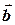и называется число 
и обозначается 
.
Смешанное произведение векторов обладает следующими свойствами:
10.  ,
| 20.  ,
|
30.  ,
| 40.  .
|
Отметим еще некоторые свойства смешанного произведения:
Три вектора 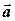, 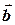и компланарны тогда и только тогда, когда их смешанное произведение равно нулю:
Если три вектора 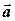, 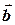и определены своими координатами в ортонормированном базисе: , , 
, то смешанное произведение вычисляется по формуле:
(2.10)
Геометрический смысл смешанного произведения: модуль смешанного произведения 
равен объёму параллелепипеда, построенного на этих векторах, как на сторонах.
Пример 2.7. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, если A (3;–2;–4), B (–5;3;4), C (1;–3;2), D (4;1;–2).
Решение. Найдем координаты векторов 
:
.
а) Объем пирамиды ABCD вычислим по формуле:
.
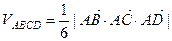Поскольку
,
то,
б) Площадь грани ABC вычислим по формуле:
.
Поскольку
,
то площадь грани ABC будет равна
в) Для того чтобы найти косинус угла между ребрами AB и AC найдем косинус угла между векторами 
и 
:
.
Тогда 
.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Уравнение прямой
Общим уравнением прямой называется уравнение
, (3.1)
полученное из уравнения
. (3.2)
Геометрический смысл общего уравнения прямой заключается в том, что оно описывает прямую, проходящую через точку 
перпендикулярно вектору 
, который называется нормальным вектором прямой
Каноническим уравнением прямой называется уравнение
. (3.3)
Геометрический смысл канонического уравнения прямой заключается в том, что оно описывает прямую, проходящую через точку параллельно вектору 
, который называется направляющим вектором прямой:
Уравнением прямой с угловым коэффициентом называется уравнение
, (3.4)
или
. (3.5)
Геометрический смысл коэффициента k – это тангенс угла наклона прямой к положительному направлению оси O x, т.е. k =tga, b – это отрезок, отсекаемый прямой на оси O y.
Пример 3.1. Определить при каких значениях a и b две прямые
(a– 1) x– 2 y– 1 = 0 и 6 x– 4 y+b= 0
а) пересекаются; б) параллельны; в) совпадают.
Решение. Две прямые L 1: 
и L 2: 
параллельны, если
.
В частности, прямые совпадают, если
.
В случае
,
прямые пересекаются. В нашем случае, из условия
находим, что две прямые совпадают, если a =4 и b =-2. Две прямые параллельные, если a =4 и b ¹-2. Если a ¹4 при любом значении b, то прямые пересекаются.
Пример 3.2. Определить при каком значении параметра t прямая
а) параллельна оси абсцисс; б) параллельна оси ординат; в) проходит через начало координат.
Решение. Прямая 
параллельна оси абсцисс, если A =0; параллельна оси ординат, если B =0; проходит через начало координат, если C =0.
В нашем случае, если 
, т.е. при 
и 
, прямые будут параллельны оси абсцисс: 
и 
.
Если 
, т.е. при 
, то прямая пройдёт параллельно оси ординат: 
.
Прямая будет проходить через начало координат, если 
, т.е. при 
: 
.
Пример 3.3. Заданы точка M (–1;2) и прямая L: –2 x + y –1=0. Написать уравнения прямых L 1 и L 2, проходящих через точку M и L 1|| L и L 2^ L.
      y
L 2
M o L
L 1 x
|
Решение. Сделаем чертеж. Чтобы построить прямую, достаточно знать две ее точки. Очевидно, что A (0;1), B (1;3)Î L. Через найденные точки проводим прямую. Прямая L задана общим уравнением прямой, тогда ее нормальный вектор имеет координаты n ={–2;1}. Поскольку L 1|| L Þ L 1^ n, то вектор n будет нормальным вектором также и для прямой L 1. Тогда используя формула (3.2), получим
–2(x +1)+(y –2)=0,
или
L 1: –2 x + y –4=0.
Поскольку L 2^ L Þ L 2|| n, то вектор n будет направляющим вектором L 2. Тогда используя формулу (3.3), получим
,
или
L 2: x +2 y –3=0.
Пример 3.4. Найти координаты точки М, лежащей на одной прямой с точками A (–1;1) и B (1;5), если абсцисса и ордината этой точки равны между собой.
Решение. Найдем уравнение прямой (АВ), воспользовавшись формулой прямой, проходящей через две точки:
.
Разделив последнее уравнение на 2, получим
(AB): 2 x–y+ 3=0.
Пусть исходная точка имеет координаты M (a;a). Так как она принадлежит прямой (AB), то ее координаты должны удовлетворять уравнению:
2 a–a+ 3=0 Þ a= –3.
Таким образом, искомая точка имеет координаты М (–3;–3).
Пример 3.5.. Из точки M (3;2) выходит луч света под углом j = arctg2 к оси O x. Найти уравнения падающего и отраженного лучей.
   y
L 2 L 1
j j K x
|
Решение. Найдем уравнение падающего луча. Эта прямая L 1 проходит через точку M с угловым коэффициентом
k 1 = tgj = 2.
Тогда используя уравнение (3.5), получим
y– 2 = 2(x –3),
или
L 1: 2 x–y– 4=0.
Это есть уравнение падающего луча. Чтобы составить уравнение отраженного луча L 2, нужно знать координаты точки отражения K и угловой коэффициент k 2. Координаты точки отражения K можно найти как точку пересечения прямой L 1 и оси O x:
Þ 
т.е. K (2;0). Угловой коэффициент k 2 найдем из того условия, что «угол падения равен углу отражения». Тогда очевидно, что j2 = 1800–j. Отсюда
k 2 = tgj2 = tg(1800–j) = –tgj = –2.
Теперь известны все параметры, чтобы записать уравнение отраженного луча:
y = – 2(x– 2),
или
L 2: 2 x + y –4=0.
