Наименьшее общее кратное нескольких натуральных чисел

Признаки делимости чисел

Ключевые слова: натуральное число, делимость чисел, признаки делимости

Если каждое слагаемое делится на некоторое число, то и сумма делится на это число.
Если в произведении хотя бы один из множителей делится на некоторое число, то и произведение делится на это число.
Натуральное число делится на 2 тогда и только тогда, когда последняя цифра делится на 2.
Натуральное число делится на 5 тогда и только тогда, когда его последняя цифра либо 0, либо 5.
Натуральное число делится на 10 тогда и только тогда, когда его последняя цифра 0.
Натуральное число, содержащее не менее трех цифр, делится на 4 тогда и только тогда, когда делится на 4 двузначное число, образованное последними двумя цифрами заданного числа.
Натуральное число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.
Натуральное число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

Основная теорема арифметики. Любое составное натуральное число можно представить единственным образом в виде произведения простых чисел.

Например, 12=2 2 3. Можно сказать, что число 12 разложено на простые множители.

Пример: Разложить на простые множители число 270

Решение:

270=2

5=2

Теорема. Если n составное число, то среди его простых делителей есть хотя бы один делитель p такой, что p2 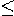n

Наибольший общий делитель нескольких натуральных чисел

Пусть даны числа 48 и 60. Выпишем все делители числа 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48. Также выпишем все делители числа 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. Среди выписанных чисел есть одинаковые: 1, 2, 3, 4, 6, 12. Все эти числа назывыаются общими делитьелями чисел 48 и 60, наибольшее среди них число 12 называется наибольшим общим делителем.

Замечание. Для того чтобы выписать все делители, надо узнать сколько их всего будет у даного числа. Для этого надо разложить число 48 на простые множители: 48=24 3. Число делителей числа 48: 4+1 1+1 =5 2=10. Т.е. степень числа 2 плюс 1 умножить на степень числа 3 плюс 1.

Для любых заданных натуральных чисел a и b можно найти наибольший общий делитель. Он обозначается HOD(a,b) и читается: " HOD от a и b ". Например, HOD(a,b) = HOD(48,60) = 12.

Взаимно простие числа. Если числа a и b таковы, что HOD(a,b) = 1, то такие числа называют зваимно простые.

Пример: Числа 26 и 35 являются взаимно простыми, хотя сами они составные. Так как 26=2 13 и 35=5 7, то HOD(26,35) = 1.

Чтобы найти наибольший общий делитель нескольких чисел, надо разложть их на простые множители, найти общие простые множители и вычислить произведение общих простых множителей, взяв каждый из них с наименьшим, из имеющихся, показателем.

Пример: Найти HOD(56,84,96)

Решение:

56=2 2 2 7=23 7

96=2 2 2 2 2 3=25 3

84=2 2 3 7=22 3 7

и тогда HOD(56,84,96) = 22 = 4

Наименьшее общее кратное нескольких натуральных чисел

Пусть даны числа 14 и 16. Выпишем все числа, кратные числа 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120. Также выпишем все числа, кратные числа 16: 16, 32, 48, 64, 80, 96, 112, 128. Среди выписанных чисел есть одинаковые: 48 и 96. Все эти числа назывыаются общими кратными чисел 14 и 12, наименьшее среди них число 48 называется наименьшим общим кратным чисел 14 и 12.

Для любых заданных натуральных чисел a и b можно найти наименьшее общее кратное. Он обозначается HOK(a,b) и читается: " HOK от a и b ". Например, HOK(a,b) = HOK(14,12) = 48.

Замечание. Любое общее кратное чисел a и b делится на HOK(a,b).

Чтобы найти наименьшее общее кратное нескольких чисел, надо разложть их на простые множители, и вычислить произведение всех простых множителей, взяв каждый из них с наибольшим, из имеющихся, показателем степени.

Пример: Найти HOK(56,84,96)

Решение: 56=2 2 2 7=23 7

96=2 2 2 2 2 3=25 7

84=2 2 3 7=22 3 7

и тогда HOK(56,84,96) = 25 3 7 = 672

Теорема. Для любых натуральных чисел a и b справедливо равенство HOD(a b) HOK(a b)=ab. Если числа a и b взаимно простые, т.е. HOD (a,b) = 1, то HOK (a,b) = ab.

Наименьшее общее кратное двух взаимно простых чисел равно произведению этих чисел.

Дроби

Ключевые слова: дробь, числитель, знаменатель, смешанное число, приведение к общему знаменателю, сложение, вычитание, умножение и деление дробей, правильная и неправильная дробь

Определение: Выражение вида ba или a: b, где а и b целые числа, b =0, называется дробью

Число a называется числителем дроби. Число b называется знаменателем дроби

Если a < b, то выражение ba правильная дробь

Если a > b, то выражение ba неправильная дробь. Из любой неправильной дроби можно выделить целую часть и дробную часть. Примеры: 67=161, 518=353

Основное свойство дроби: Две дроби ba и cd называются равными если a d=b c.

Действия над дробями (ba и cd):

ba=b ka k - Дробь не изменится, если числитель и знаменатель дроби умножить на одно и то же число

Если b = d, то ba cd=ba c

Если b =d, то дроби нужно привести к общему знаменателю: ba cd=bdad cb. Общим знаменателем будет НОК (b, d)

Если k целое число, то k ba=bk a или ba:k=ab k

Две дроби можно умножать ba cd=a cb d или делить ba:cd=b ca d

Операции над числами

Свойства сложения:

a + b = b + a - переместительное свойство

(a + b) +c = a + (b + c) - сочетательное свойство

a + 0 = a - свойство нуля

a + (-a) = 0 - сумма противоположных чисел

Свойства вычитания:

a - (b + c) = a - b - c вычитание суммы чисел от числа

(a + b) - c = (a - c) + b = a + (b - c) - вычитание числа от суммы

a - 0 = a - свойство нуля

0 - a = -a - свойство нуля

Свойства умножения:

a· b = b· a - переместительное свойство

(a · b)· c = a· (b · c) -сочетательное свойство

(a - b)· c = a · c - b · c - распределительное свойство

(a + b)· c = a · c + b · c - распределительное свойство

a · 1 = a - свойство единицы

a · 0 = 0 - свойство нуля

a a1=1 a =0 - свойство обратных чисел

Свойства деления:

(a · b): c = a · (b: c) = (a: c) · b - деления произведения на число

(a + b): c = a: c + b: c - деление суммы на число

(a - b): c = a: c - b: c - деление разности на число

a: (b ·c) = (a: b):c = (a: c): b - деление числа на произведение

a: 1 = a; 0: a = 0; a: a = 1, a =0- свойство единицы и нуля

Процент. Сложный процент

Ключевые слова: процент, сложный процент

Процентом называется сотая часть от числа, т.е. 1%А = 0,01А

1% = 0,01, 2% = 0,02, 45% = 0,45, 350% = 3,5. Часто встречающиеся проценты: 5% = 0,05 = 120, 10% = 0,1 = 110, 20% = 0,2 = 51, 25% = 0,25 = 41, 50% = 0,5 = 21, 75% = 0,75 =43

Основные типы задач.

Сколько процентов составляет число А от числа В? Решение: x=ВА 100%

Число А увеличилось на 20%, а затем полученное число уменьшилось на 25%. Как, в итоге, изменилось исходное число? Решение: 1) А₁= (100% + 20%)А = 120%А = 1,2А 2) А₂= (100% - 25%)А₁ = 75%А₁ = 0,75А₁ = 0,75 1,2А = 0,9А = 90%А 3) А₂ - А = 90%А - 100%А = -10%. Ответ: число уменьшилось на 10%.

Как изменится время, если скорость движения увеличится на 25%? Решение: 1) t=SV 2) t1=SV1=S1 25V=11 25SV=0 8SV=80%t. Ответ: уменьшится на 20%.