В первой лекции был рассмотрен принцип относительности Галилея, который утверждал, что промежутки времени, расстояния и ускорения инвариантны т.е. одинаковы во всех инерциальных системах отсчёта. Легко показать, что инвариантны и силы, действующие на материальную точку, а следовательно второй и третий законы Ньютона.
В общем случае принцип относительности Галилея можно записать следующим образом: законы механики одинаковы во всех инерциальных системах отсчёта (механический принцип относительности).
После того как во второй половине ХIХ в. Максвеллом были сформулированы основные законы электродинамики, возник вопрос: распространяется ли принцип относительности, справедливый для механических явлений, и на электромагнитные процессы, одинаково во всех инерциальных системах отсчёта.
В электродинамике Максвелла скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям и равна с = 3.108 м/с. Но с другой стороны, в соответствии с законом сложения скоростей, вытекающем из преобразований Галилея, скорость может равняться с только в одной избранной системе отсчёта.
В 1905 г. А.Эйнштейн в работе «К электродинамике движущихся тел» был дан ответ на поставленный выше вопрос.
В специальной теории относительности (СТО) также как в классической механике предполагается, что время однородно, а пространство однородно и изотропно.
Первый постулат СТО (релятивистский принцип относительности Эйнштейна): в любых инерциальных системах отсчёта все физические явления при одних и тех же условиях протекают одинаково, т.е. физические законы инвариантны по отношению к выбору инерциальной системы отсчёта, а уравнения, выражающие эти законы, имеют одинаковую форму во всех инерциальных системах отсчёта.
Второй постулат СТО выражает принцип инвариантности скорости света: скорость света в вакууме не зависит от движения источника света, она одинакова во всех направлениях и во всех инерциальных системах отсчёта. Опыт показывает, что скорость света в вакууме с – предельная скорость в природе: скорость любых тел, а также скорость распространения любых сигналов и взаимодействий не может превосходить с.
Постоянство скорости света приводит к тому, что понятие одновременности, считающееся в ньтоновской механике абсолютным, в действительности является относительным.
Пример с поездом
Световой сигнал из середины поезда для пассажира поезда (в системе отчёта К *) приходит в точки 1 и 2 одновременно, а для наблюдателя, находящегося на платформе (в системе отсчёта К) точка1 движется навстречу сигналу, а точку 2 сигналу приходится «догонять».
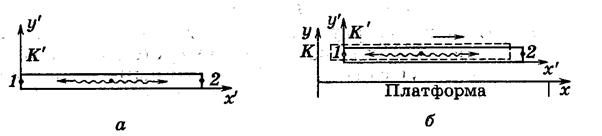
Таким образом в разных системах отсчёта время течёт неодинаково.
Чтобы описать «точечное» событие (например, распад элементарной частицы) нужно указать, в каком месте и в какой момент времени оно происходит. Эта задача может быть осуществимой, если создать в пространстве равноотстоящие координатные метки и совместить с каждой такой меткой часы. Синхронизацию часов можно сделать, посылая от одних часов к другим световой согнал.
Постоянство скорости света приводит к тому, что пространство и время оказываются взаимносвязанными, образуя единое пространство-время. Эта взаимосвязь может быть представлена в виде виртуального четырёхмерного пространства
Х, у, z, ct.
Преобразования Лоренца
.
Подобно тому как классические представления о пространстве и времени формулируются количественно с помощью преобразований Галилея для координат и времени, новые релятивистские представления о пространстве и времени формулируются с помощью преобразований Лоренца.
Пусть имеется инерциальная система отсчёта К. координаты любой точки, например, точки В, в этой системе обозначим через х, у, z, а время через t. Другая инерциальная система К* движется с постоянной скоростью 
относительно системы К, а оси y* и z* параллельны соответствующим осям y и z (это означает рассмотрение частных преобразований, а не общих). Начало отсчёта времени выбраны таким образом, чтобы в момент времени t = 0 точки О и О* совпадали.
и 
в К-системе
в К*-системе. Следовательно
, где
– некоторая константа.
Аналогично: 
в К*-системе
в К-системе и
.
Из равноправия систем К и К* вытекает, что коэффициент пропорциональности в обоих случаях должен быть один и тот же.
Для произвольной точки В получаем
Для нахождения коэффициента используем 2-ой постулат СТО. Пусть в момент времени t = t* = 0 в направлении осей х и х* посылается световой сигнал, который производит вспышку на экране в точке В. Это событие описывается координатой х и моментом t в системе К и координатой х* и моментом t* в системе К*, причём
и 
, тогда
Перемножив два последних уравнения, получаем
или 
.
Для координат получаем
и 
, где
.
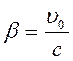Для получения формулы, определяющей t по известным t* и х* исключаем координату х из исходной системы уравнений
или
Так же получают
.
Зависимости 
; 
; 
и 
называют преобразованиями Лоренца.
В пределе, при 
и при β << 1 преобразования Лоренца практически не отличаются от преобразований Галилея.
Различие в течение времени в разных системах отсчёта обусловлено существованием предельной скорости распространения взаимодействий.
При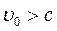 
выражения для 
становятся мнимыми. В этом проявляется то обстоятельство, что движение со скоростями, большими с невозможно.
Для запоминания удобна следующая запись
.
Кинематические следствия из преобразований Лоренца
1). Одновременность событий в разных системах отсчёта
Пусть в системе К в точках х 1 и х 2 происходят одновременно два события в момент времени t 1 = t 2 = τ. Тогда в системе К* этим событиям будут соответствовать моменты
и 
т.е.
если в К-системе события пространственно разобщены, то в К*-системе они не будут одновременными 
.
Это означает, что в одних системах событие 1 будет предшествовать событию 2, а в других системах может быть наоборот. Сказанное относится лишь к событиям, между которыми отсутствует причинная связь. (Рождение элементарной частицы во всех системах отсчёта происходит раньше её распада и ни в одной из систем ребёнок не рождается раньше его родителей).
