Прилади: тверде тіло правильної геометричної форми (циліндр),
ваги з важком, мікрометр, штангенциркуль.
Ноніус
Ноніусом називається прилад, який служить для визначення з точністю до частин міліметра довжин прямолінійних відрізків (лінійний ноніус) чи довжин кругових дуг, якими виміряються кути, які опираються на них (круговий чи кутовий ноніус).
Лінійний ноніус є доповненням до звичайної шкали. Він являє собою невелику лінійку, що ковзає уздовж основної шкали (рис. 1). На цій лінійці нанесена шкала, що складається з m розподілів. Сумарна довжина всіх її m розподілів дорівнює (m - 1) найменших розподілів основної шкали, тобто
, (1)
де x і y – ціна розподілів ноніуса й основної шкали відповідно.
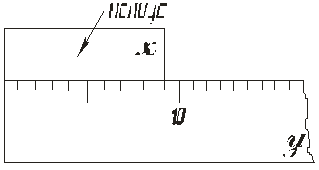
Рис.1
Рис.2
Звідси
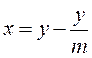, (2)
а різниця в ціні розподілів шкали і ноніуса
, (3)
де α - точність ноніуса, визначає собою максимальну погрішність ноніуса.
Розглянемо процес виміру за допомогою ноніуса. Нехай L - вимірюваний відрізок (рис. 2). Розташуємо на його початку нульовий розподіл основної шкали. Кінець виявиться між К та (К+1) розподілами цієї шкали. Тоді
,
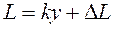де ∆L < - невідома частка (К+1) розподілу шкали.
Прикладемо тепер до кінця відрізка L нуль ноніуса. Тому що розподіли ноніуса не дорівнюють розподілам основної шкали, то знайдеться розподіл n ноніуса, що буде ближче усього до (К+n) розподілу основної шкали. Якби ці розподіли зійшлися, то, як видно з рис. 2,
, (5)
звідси
, (6)
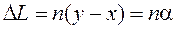, (7)
вся довжина дорівнює
, (8)
чи згідно з (3)
, (9)
що можна сформулювати так: довжина відрізка, вимірювана за допомогою ноніуса, дорівнює числу цілих розподілів основної шкали до нуля ноніуса, помноженому на ціну розподілу основної шкали, плюс точність ноніуса (зазначеного на приладі), помножена на номер розподілу ноніуса, що співпадає з будь-яким розподілом основної шкали.
Штангенциркуль
Штангенциркуль (рис.3) служить для виміру довжин, зовнішніх і внутрішніх діаметрів трубок і глибин отворів. Складається з розділеної на міліметри шкали LM, уздовж якої може переміщатися ніжка В з рамкою Д, яка фіксується гвинтом С та хвостом К. В обоймі рамки проти розподілів шкали зроблений виріз, на скошеному краї якого, що прилягає до шкали, нанесений ноніус; коли ніжки зсунуті впритул, то «0» ноніуса збігається з «0» шкали. Нерухома ніжка LA служить упором при вимірі довжини тіла.
Вимір. Розсунувши ніжки штангенциркуля, поміщають між ними вимірюване тіло; ніжку підводять так, щоб тіло було злегка затиснуте, і роблять відлік. Тому що ніжка В, а отже, і «0» ноніуса перемістилися на довжину вимірюваного тіла, то відраховують на шкалі ціле число міліметрів до «0» ноніуса і дивляться, яка дільниця ноніуса збігається з деякою дільницею шкали LM.
Помножимо це число на точність ноніуса (яка зазначена на приладі), додаємо до відліку за шкалою LM.
Для вимірів глибин отворів служить хвіст ДО, що задвигається у вимірювану глибину. Відлік у цьому випадку робимо так само, як зазначено вище.
Рис.3
Мікрометр
Мікрометр (рис.4) служить для виміру діаметра дроту, невеликих товщин пластинок і т.ін. Він має вигляд тисків, у яких вимірюваний об'єкт затискується за допомогою гвинта.
Хід гвинта дорівнює 0,5 мм. На гвинті укріплений барабан В з нанесеною на ньому шкалою, що має 50 розподілів. При затиснутому гвинті «0» барабана стоїть проти «0» шкали, що нанесена на корпус тисків С. Ця шкала має два масштаби: верхній і нижній. Нижній стосовно верхнього здвигнутий на 0,5 мм. Вимірюваний предмет поміщають між гвинтом і упором. Потім доводять гвинт до зіткнення з досліджуваним предметом і починають відлік. По нерухомій шкалі відраховуються міліметри, а по шкалі барабана – соті частки міліметра. Через те, що хід гвинта дорівнює 0,5 мм, при записуванні відліку можуть бути два випадки.
Рис.4
Вимірюваний предмет має довжину, рівну а міліметрам і декільком сотим часткам міліметра, що лежать в інтервалі («а» мм) і («а» +0,5); у цьому випадку соті частки міліметра прямо приписуються «а» мм (рис.6).
Вимірюваний предмет має довжину, рівну («а» +0,5) мм і декільком сотим часткам його, що лежать в інтервалі («а» + 0,5) мм -... («а» +1) мм. У цьому випадку соті частки міліметра приписуються до («а» +0,5) мм (рис. 5). Із того, 1-й чи 2-й випадок має місце, судять за верхньою шкалою: якщо край барабана стоїть ближче до розподілу нижньої основної шкали, то це є 1-й випадок; якщо до розподілу верхньої, то 2-й випадок.
Головним джерелом помилок є нерівномірність натискання гвинта на вимірюваний предмет. Для усунення цього недоліку сучасні мікрометри забезпечуються спеціальним пристроєм – трещіткою D, що не допускає занадто сильного натискання. Дія трещітки заснована на терті, що виникає між стрижнем гвинта С та рукояткою А, за якою він обертається.
Рис. 5 Рис. 6
Теоретичні відомості
Густиною речовини називається фізична величина, вимірювана масою речовини в одиниці об'єму. Густина речовини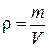 
, де m – маса тіла, V – його об’єм.
Цей вираз справедливий лише для однорідних тіл. У неоднорідних тілах щільність різних ділянок неоднакова. Тому обирають малий об’єм ∆V, усередині якого тіло вважається однорідним. Тоді щільність 
. Переходячи до межі, одержимо 
.
У міжнародній системі одиниць за одиницю щільності приймають щільність такої речовини, 1 м3 якої має масу 1 кг. Найменування одиниці щільності в SI 1кг/м3.
У даній роботі визначається щільність металевого тіла, що має форму циліндра. Об’єм суцільного циліндра дорівнює 
, де d – його діаметр, h – висота.
Порядок виконання роботи
1) Ознайомитися з вимірювальними приладами, установити їхню точність.
2) Масу циліндра визначити зважуванням на технічних вагах (зважувати один раз).
3) Діаметр циліндра вимірювати мікрометром, висоту циліндра – штангенциркулем (вимір проводити по п'ять разів).
4) Результати вимірів занести в таблицю.
5) Визначити щільність зразка за формулою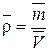 
, де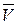 
= 0,78 
.
Таблиця
| № п/п | hi | ∆hi | ∆hi 2 | di | ∆di | ∆di2 | 
| 
| r | er | s, % | r |
6) Обчислити довірчий інтервал 
при вимірі ρ.
Для цього знайти відносну помилку за формулою
,
де 
- довірчі інтервали маси m, діаметра d, висоти h,
, y = 0,5 ціни розподілу при Р = 0,95,
;
; 
;
тоді 
.
Результати записати у вигляді:
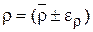при 
, 
.
Контрольні запитання
1) Що таке густина речовини?
2) Якими методами вимірюється щільність т
вердих речовин, рідин і газів?
3) Чому рекомендуються виміри однієї і тієї ж величини робити в різних місцях циліндра?
4) Як обчислюється довірчий інтервал?
5) Які правила округлення при запису результату вимірів?
Лабораторна робота № 2
