ВВЕДЕНИЕ
Скорость и ускорение прямолинейного движения в общем случае определяются формулами
u =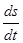 
, a = 
В случае прямолинейного равномерного движения
u = 
= const, a = 0.
Для прямолинейного равнопеременного движения
s =u 0 t +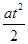 
, u = u 0 + at, a = const.
В этих уравнениях ускорение a положительно при pавноускоренном движении и отрицательно при pавнозамедленном.
При криволинейном движении полное ускорение
a = 
.
Здесь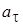 
— тангенциальное (касательное) ускорение и 
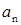— нормальное (центростремительное) ускорение, причём
= 
, = 
,
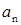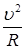где u — скорость движения и R — радиус кривизны траектории в данной точке.
При вращательном движении в общем случае угловая скорость и угловое ускорение находятся по формулам
w = 
, e =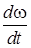 
= 
.
В случае равномерного вращательного движения угловая скорость
w=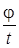 
= 
= 2p n,
где T — период вращения, n — частота вращения, т.е. число оборотов в единицу времени.
Угловая скорость w связана с линейной скоростью u соотношением
u = w R.
Тангенциальное и нормальное ускорения при вращательном движении могут быть выражены в виде
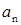= e R, =w2 R
Основной закон динамики (второй закон Ньютона) выражается уравнением
F dt = d(mu).
Если масса m постоянна, то
F = m = ma,
где a — ускорение, которое приобретает тело массой m под действием силы F.
Работа силы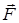 
на пути s может быть выражена формулой
A = 
,
где Fs — проекция силы на элементарное перемещение d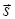 
, ds — длина элементарного перемещения. Интегрирование должно быть распростра-нено на весь путь s. В случае постоянной силы, действующей под углом a к перемещению, имеем
A = F s сosa,
где a — угол между силой 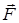и перемещением .
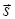Мощность определяется формулой
.
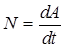В случае постоянной мощности
.
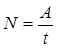Здесь A — работа, совершаемая за время t. Мощность может быть определена также формулой
N = Fu сosa,
т.е. произведением скорости движения на проекцию силы на направление движения.
Для кинетической энергии тела массой m, движущегося со скоростью u, имеем
.
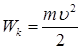Формулы для потенциальной энергии имеют разный вид в зависимости от характера действующих сил.
Импульс замкнутой механической системы постоянен при любых взаимодействиях тел системы, т.е.
+ 
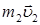+¼+ 
= const.
Полная механическая энергия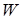 
системы, между телами которой действуют консервативные силы, постоянна, т.е.
= 
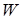= const,
где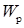 
— потенциальная энергия системы.
Работа A неконсервативных сил равна изменению механической энергии системы, т.е. A = 
, 
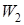и 
— механическая энергия системы в конечном и начальном состоянии.
При криволинейном движении сила, действующая на материальную точку, может быть разложена на две составляющие — тангенциальную и нормальную. Нормальная составляющая
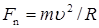
является центростремительной силой. Здесь u — линейная скорость движения тела массой m, R — радиус кривизны траектории в данной точке.
Сила, вызывающая упругую деформацию x, пропорциональна деформации, т.е.
F = k x,
где k — жёсткость (коэффициент, численно равный силе, вызывающей деформацию, равную единице).
Потенциальная энергия упругого тела
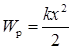
Две материальные точки (т.е. такие тела, размеры которых малы по сравнению с их взаимным расстоянием) притягиваются друг к другу с силой
,
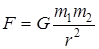где G = 6,672×10–11 Н×м/кг2 — гравитационная постоянная, m 1 и m 2— массы взаимодействующих материальных точек, r — расстояние между ними. Этот закон справедлив и для однородных шаров; при этом r — расстояние между их центрами масс.
Потенциальная энергия гравитационного взаимодействия тел
.
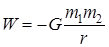Знак "минус" соответствует тому, что при r = ¥ потенциальная энергия двух взаимодействующих тел равна нулю; при сближении этих тел потенциальная энергия убывает.
Момент M силы F относительно какой-нибудь оси вращения определяется формулой
M = F l,
где l — расстояние от прямой, вдоль которой действует сила, до оси вращения.
Моментом инерции материальной точки относительно какой-нибудь оси вращения называется величина
I = m r2,
где m — масса материальной точки и r — её расстояние до оси вращения.
Момент инерции твёрдого тела относительно оси его вращения
,
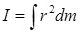где интегрирование должно быть распространено на весь объём тела. Производя интегрирование, можно получить момент инерции тела любой формы.
Момент инерции сплошного однородного цилиндра (диска) относительно оси цилиндра
,
где R — радиус цилиндра и m — его масса.
Момент инерции полого цилиндра (обруча) с внутренним радиусом R 1 и внешним R 2 относительно оси цилиндра
,
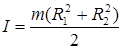для тонкостенного полого цилиндра R 1» R 2 = R и I» mR 2.
Момент инерции однородного шара радиусом R относительно оси, проходящей через его центр:
.
Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно к нему,
.
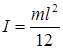Если для какого-либо тела известен его момент инерции I c относительно любой оси, проходящей через его центр масс, то момент инерции I относительно любой оси, параллельной первой, может быть найден по формуле Штейнера
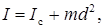
где m — масса тела и d — расстояние от центра масс тела до оси вращения.
Основной закон динамики вращательного движения выражается уравнением
M×dt = dL = d (I w),
где M — момент сил, приложенный к телу, L — момент импульса тела (I — момент инерции тела, w — его угловая скорость). Если I = const, то
,
где e — угловое ускорение, приобретаемое телом под действием момента сил M.
Кинетическая энергия вращающегося тела
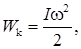
где I — момент инерции тела и w — его угловая скорость.
ЗАДАЧИ
1 (1.2). Первую половину своего пути автомобиль двигался со скоростью u 1 = 80 км/ч, а вторую половину со скоростью u 2 = 40 км/ч. Какова средняя скорость u движения автомобиля?
2 (1.8). Тело, брошенное вертикально вверх, вернулось на землю через время t = 3 с. Какова была начальная скорость u 0 тела и на какую высоту h оно поднялось?
3 (1.9). Камень бросили вертикально вверх на высоту h = 10 м. Через какое время t он упадёт на землю? На какую высоту h поднимется камень, если начальную скорость камня увеличить вдвое?
4 (1.10). С аэростата, находящегося на высоте h = 300 м, упал камень. Через какое время t камень достигнет земли, если: а) аэростат поднимается со скоростью u = 5 м/с; б) аэростат опускается со скоростью u = 5 м/с; в) аэростат неподвижен?
5 (1.12). Тело падает с высоты h = 19,6м с начальной скоростью u 0 = 0. Какой путь пройдёт тело за первую и последнюю 0,1 с своего движения?
6 (1.14). Свободно падающее тело в последнюю секунду движения проходит половину всего пути. С какой высоты падает тело и каково время t его падения?
7 (1.16). Расстояние между двумя станциями метрополитена l = 1,5 км. Первую половину этого расстояния поезд проходит равноускоренно, вторую — равнозамедленно с тем же по модулю ускорением. Максимальная скорость поезда u = 50 км/ч. Найти ускорение a и время t движения поезда между станциями.
8 (1.18). Поезд, двигаясь равнозамедленно, в течение времени t = 1 мин уменьшает свою скорость от u 1 = 40 км/ч до u 2 = 28 км/ч. Найти ускорение a поезда и расстояние s, пройденное им за время торможения.
9 (1.19). Поезд движется равнозамедленно, имея начальную скорость u 0 = 54 км/ч и ускорение a = –0,5 м/с2. Через какое время t и на каком расстоянии s от начала торможения поезд остановится?
10 (1.20). Тело 1 движется равноускоренно, имея начальную скорость u 10 и ускорение a 1. Одновременно с телом 1 начинает двигаться равнозамедленно тело 2, имея начальную скорость u 20 и ускорение a 2. Через какое время после начала движения оба тела будут иметь одинаковую скорость?
11 (1.22). Зависимость пройденного телом пути s от времени t даётся уравнением 
, где A = 2 м/с, B = 3 м/с2 и C = 4 м/с3. Найти: а) зависимость скорости u и ускорения a от времени t; б) расстояние s, пройденное телом, скорость и ускорениетела через время t = 2 с после начала движения.
12 (1.24). Зависимость пройденного телом пути s от времени t даётся уравнением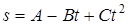 
, где A = 3 м, B = 2 м/с и C = 2 м/с2. Найти среднюю скорость u ср и среднее ускорение a ср тела за первую, вторую и третью секунды его движения.
13 (1.26). С башни высотой h = 25 м горизонтально брошен камень со скоростью u = 15 м/с. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадёт на землю? С какой скоростью он упадёт на землю? Какой угол j составит траектория камня с горизонтом в точке его падения на землю?
14 (1.27). Камень, брошенный горизонтально, упал на землю через время t = 0,5 c на расстоянии l = 5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью он брошен? С какой скоростью он упадёт на землю? Какой угол составит траектория камня с горизонтом в точке его падения на землю?
15 (1.28). Мяч, брошенный горизонтально ударяется о стенку, находящуюся на расстоянии l = 5 м от места бросания. Высота места удара мяча о стенку на D h = 1 м меньше высоты h, с которой брошен мяч. С какой скоростью u брошен мяч? Под каким углом мяч подлетает к поверхности стенки?
16 (1.29). Камень, брошенный горизонтально, через время t = 0,5 с после начала движения имел скорость u в 1,5 раза большую скорости u x в момент бросания. С какой скоростью u x брошен камень?
17 (1.32). Мяч брошен со скоростью u 0 = 10 м/с под углом a = 40° к горизонту. На какую высоту поднимется мяч? На каком расстоянии l от места бросания он упадёт на землю? Какое время t он будет в движении?
18 (1.33). На спортивных состязаниях в Ленинграде спортсмен толк-нул ядро на расстояние l 1 = 16,2м. На какое расстояние l 2 полетит такое же ядро в Ташкенте при той же начальной скорости и при том же угле наклона её к горизонту? Ускорение свободного падения в Ленинграде g 1 = 9,819 м/с2, в Ташкенте g 2 = 9,801 м/с2.
19 (1.35). Камень, брошенный со скоростью u 0 = 12 м/с под углом a = 45° к горизонту, упал на землю на расстоянии l от места бросания. С какой высоты h надо бросить камень в горизонтальном направлении, чтобы при той же начальной скорости он упал на то же место?
20 (1.40). Мяч, брошенный со скоростью u 0 = 10 м/с под углом a = 45° к горизонту, ударяется о стенку, находящуюся на расстоя нии l = 3 м от места бросания. Когда происходит удар мяча о стенку (при подъёме мяча или при его опускании)? На какой высоте h мяч ударит о стенку (считая от высоты, с которой брошен мяч)? Найти скорость u мяча в момент удара.
§ 2. КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
1 (1.41). Найти угловую скорость: а) суточного вращения Земли; б) часовой стрелки на часах; в) минутной стрелки на часах; г) искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т = 88 мин. Какова линейная скорость u движения этого искусственного спутника, если известно, что его орбита расположена на расстоянии h = 200 км от поверхности Земли?
2 (1.44). Ось с двумя дисками, расположенными на расстоянии l = 0,5 м друг от друга, вращается с частотой n =1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; при этом отверстие от пули во втором диске смещено относительно отверстия в первом диске на угол j = 12°. Найти скорость u пули.
3 (1.45). Найти радиус R вращающегося колеса, если известно, что линейная скорость u точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на расстоянии l = 5 см ближе к оси колеса.
4 (1.46). Колесо, вращаясь равноускоренно, достигло угловой скорости w = 20 рад/с через N = 10 об после начала вращения. Найти угловое ускорение колеса.
5 (1.47). Колесо, вращаясь равноускоренно, через время t = 1 мин после начала вращения приобретает частоту n = 720 об/мин. Найти угловое ускорение колеса и число оборотов N колеса за это время.
6 (1.48). Колесо, вращаясь равнозамедленно, за время t = 1 мин уменьшило свою частоту с n 1 = 300 об/мин до n 2 = 180 об/мин. Найти угловое ускорение колеса и число оборотов N колеса за это время.
7 (1.49). Вентилятор вращается с частотой n = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки?
8 (1.50). Вал вращается с частотой n = 180 об/мин. С некоторого момента вал начал вращаться равнозамедленно с угловым ускорением e = 3 рад/с2. Через какое время t вал остановится? Найти число оборотов N вала до остановки.
9 (1.51). Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением a t= 5 см/с2. Через какое время после начала движения нормальное ускорение a nточки будет: а) равно тангенциальному; б) вдвое больше тангенциального?
10 (1.52). Точка движется по окружности радиусом R = 10 см с поcтоянным тангенциальным ускорением a t. Найти тангенциальное ускорение a t точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки u = 79,2 см/с.
11 (1.53). Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением a t. Найти нормальное ускорение a nточки через время t = 20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки u = 10 см/с.
12 (1.54). В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью u. Найти угловую скорость вращения электрона вокруг ядра и его нормальное ускорение a n. Считать радиус орбиты r = 0,5×10 – 10 м и линейную скорость электрона на этой орбите u = 2,2 106 м/с.
13 (1.55). Колесо радиусом R = 10 см вращается с угловым ускоре-нием e = 3,14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость w; б) линейную скорость u; в) тангенциальное ускорение a t; г) нормальное ускорение a n; д) полное ускорение a; е) угол a, составляемый вектором полного ускорения с радиусом колеса.
14 (1.56). Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени даётся уравнением 
, где C = 0,1 см/с3. Найти нормальное a n и тангенциальное a tускорения точки в момент, когда линейная скорость точки u = 0,3 м/с.
15 (1.57). Точка движется по окружности так, что зависимость пути от времени даётся уравнением 
, где B = 2 м/с и C = 1 м/с2. Найти линейную скорость u точки, её тангенциальное a t, нормальное a nи полное a ускорения через время t = 3 c после начала движения, если известно, что при t = 2 с нормальное ускорение точки a n= 0,5 м/с2.
16 (1.58). Найти угловое ускорение колеса, если известно, что через время t = 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол a = 60° с вектором её линейной скорости.
17 (1.59). Колесо вращается с угловым ускорением e = 2 рад/с2. Через время t = 0,5 с после начала движения полное ускорение колеса a = 13,6 см/с2. Найти радиус колеса.
18 (1.60). Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени даётся уравнением 
, где B = 2 рад/с и C = 1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловую скорость; б) линейную скорость u; в) угловое ускорение; д) тангенци-альное a tи нормальное a nускорения.
19 (1.61). Колесо радиусом R = 5 см вращается так, что зависимость угла поворота радиуса колеса от времени даётся уравнением 
где D = 1 рад/с3. Для точек, лежащих на ободе колеса, найти изменение тангенциального ускорения D a tза единицу времени.
20 (1.63). Колесо вращается так, что зависимость угла поворота радиуса колеса от времени даётся уравнением 
где B = 1 рад/с, C = 1 рад/с2 и D = 1 рад/с3. Найти радиус R колеса, если известно, что к концу второй секунды движения для точек, лежащих на ободе колеса, нормальное ускорение a n=3,46 102 м/с2
ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
1 (2.1). Какой массы m балласт надо сбросить с равномерно опускающегося аэростата, чтобы он начал равномерно подниматься с той же скоростью? Масса аэростата с балластом M = 1600 кг, подъёмная сила аэростата F = 12 кН. Считать силу сопротивления F сопр воздуха одной и той же при подъёме и при спуске.
2 (2.3). Стальная проволока некоторого диаметра выдерживает силу натяжения T = 4,4 кН. С каким наибольшим ускорением a можно поднимать груз массой m = 400 кг, подвешенный на этой проволоке, чтобы она не разорвалась?
3 (2.5). К нити подвешена гиря. Если поднимать гирю с ускоре нием a 1= 2 м/с2, то сила натяжения нити T 1 будет вдвое меньше той силы натяжения T 2 при которой нить разрывается. С каким ускорением a 2надо поднимать гирю, чтобы нить разорвалась?
4 (2.6). Автомобиль массой m = 1020 кг, двигаясь равнозамедленно, останавливается через время t = 5 с, пройдя путь s = 25 м. Найти начальную скорость u 0 автомобиля и силу торможения F.
5 (2.7). Поезд массой m = 500 т, двигаясь равнозамедленно в течение времени t = 1 мин уменьшает свою скорость от u 1 = 40 км/ч до u 2 = 28 км/ч. Найти силу торможения F.
6 (2.9). Какую силу F надо приложить к вагону, стоящему на рельсах, чтобы вагон стал двигаться равноускоренно и за время t = 30 с прошёл путь s = 11 м? Масса вагона m = 16 т. Во время движения на вагон действует сила трения F тр, равная 0,05 действующей на него силы тяжести mg.
7 (2.11). Вагон массой m = 20 т движется равнозамедленно, имея начальную скорость u 0 = 54 км/ч и ускорение a = – 0,3 м/с2. Какая сила торможения действует на вагон? Через какое время t вагон остановится? Какое расстояние s вагон пройдёт до остановки?
8 (2.12). Тело массой m = 0,5 кг движется прямолинейно, причём зависимость пройденного телом пути s от времени t даётся уравнением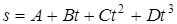 
, где C = 5 м/с2 и D = 1 м/с3. Найти силу F, действующую на тело в конце первой секунды движения.
9 (2.14). Тело массой m = 0,5 кг движется так, что зависимость пройденного телом пути s от времени даётся уравнением s = A sinw t, где A = 5 см и w = p рад/с. Найти силу F, действующую на тело через время 1/6 с после начала движения.
10 (2.15). Молекула массой m = 4,65×10 – 26 кг, летящая по нормали к стенке сосуда со скоростью u = 600 м/с, ударяется о стенку и упруго отскакивает от неё без потери скорости. Найти импульс силы F×t, полученный стенкой за время удара.
11 (2.16). Молекула массой m = 4.65×10 – 26 кг, летящая со скоростью u = 600 м/с, ударяется о стенку сосуда под углом a = 60° к нормали и упруго отскакивает от неё без потери скорости. Найти импульс силы полученный стенкой за время удара.
12 (2.19). Трамвай, трогаясь с места, движется с ускорением a = 0,5 м/с2. Через время t = 12 с после начала движения мотoр выключается и трамвай движется до остановки равнозамедленно. Коэффициент трения на всем пути k = 0,01. Найти наибольшую скорость и время t движения трамвая. Каково его ускорение a при равнозамедленном движении? Какое расстояние s пройдёт трамвай за время движения?
13 (2.20). На автомобиль массой m = 1 т во время движения действует сила трения F тр, равная 0,1 действующей на него силы тяжести mg. Какова должна быть сила тяги F, развиваемая мотором автомобиля, чтобы автомобиль двигался а) равномерно; б) с ускорением a = 2 м/с2?
14 (2.22). Шар на нити подвешен к потолку трамвайного вагона. Вагон тормозится, и его скорость за время t = 3 с равномерно уменьшается от u 1 = 18 км/ч до u 2 = 6 км/ч. На какой угол a отклонится при этом нить с шаром?
15 (2.23). Вагон тормозится, и его скорость за время t = 3,3 с равномерно уменьшается от u 1 = 47,5 км/ч до u 2 = 30 км/ч. Каким должен быть предельный коэффициент трения k между чемоданом и полкой, чтобы чемодан при торможении начал скользить по полке?
16 (2.25). На автомобиль массой m = 1 т во время движения действует сила трения F тр, равная 0,1 действующей на него силы тяжести mg. Найти силу тяги F, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью: а) в гору с уклоном 1 м на каждые 25 м пути; б) под гору с тем же уклоном.
17 (2.26). На автомобиль массой m = 1 т во время движения действует сила трения F тр, равная 0,1 действующей на него силы тяжести mg. Найти силу тяги F, развиваемую мотором автомобиля, если автомобиль движется с ускорением a = 1 м/с2 в гору с уклоном 1 м на каждые 25 м пути.
18 (2.30). Две гири с массами m 1 = 2 кг и m 2 = 1 кг cоединены нитью и перекинуты через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити T. Трением в блоке и массой блока пренебречь.
19 (2.31). Невесомый блок укреплён на конце стола. Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью и перекинуты через блок. Коэффициент трения гири 2 о стол k = 0,1. Найти ускорение a, с которым движутся гири, и силу натяжения нити T. Трением в блоке и массой блока пренебречь.
