Участок АВ
Проводим поперечное сечение 1-1 на произвольно выбранном расстоянии Х1 от сечения А, (
). Строим расчетную схему «отсеченной» части балки (рис.2.1), при этом действие «оставшейся» части на «отсеченную» заменяем крутящим моментом. (Согласно теории сопротивления материалов при кручении в поперечном сечении балки возникает только крутящий момент 
сопротивления.)
Рис.2.1
Уравнение равновесия моментов
Из уравнения равновесия
М1=М=50 кНм
Согласно полученному выражению момент сил сопротивления на первом участке не зависит от координаты Х1, эпюра М1 – прямая линия, параллельная оси Х, (рис.2).
Участок ВС
Проводим поперечное сечение 2-2 на произвольно выбранном расстоянии Х2 от сечения А (
). Строим расчетную схему «отсеченной» части балки, (рис.2.2).
Рис.2.2
Уравнение равновесия «отсеченной» части балки
Из уравнения равновесия
Эпюра момента М2 – прямая линия, параллельная оси Х, (рис.2).
Участок СД
Проводим поперечное сечение 3-3 на произвольно выбранном расстоянии Х3 от сечения А (
). Строим расчетную схему «отсеченной» части балки, (рис.2.3).
Рис.2.3
Уравнение равновесия «отсеченной» части балки
Из уравнения равновесия
Эпюра момента М3 – прямая линия, параллельная оси Х,(рис.2).
3. Определяем опасное сечение вала. Вал имеет постоянное поперечное сечение, поэтому опасным является сечение участка с наибольшим крутящим моментом. Согласно эпюре моментов опасными являются все сечения участка ВС
.
4. Находим диаметр вала из условия прочности при кручении
,
где 
- полярный момент сопротивления бруса круглого сечения.
Отсюда находим формулу для определения диаметра вала
мм.
Принимаем диаметр вала равным 190 мм.
4. Определяем углы закручивания ji на участках вала по выражению
(1)
где МKi - крутящий момент на i - том участке вала; 
- длина участка вала; JP - полярный момент инерции участка вала, который является геометрической характеристикой поперечного сечения вала и определяется по формуле:
мм4.
Подставляя значения величин в (1), определяем углы закручивания на участках вала:
- на третьем участке:
- на втором участке:
,
- на первом участке
.
Построение эпюры углов закручивания a начинаем от заделки, где угол закручивания равен нулю, далее углы суммируются с их значениями на предыдущих участках. Таким образом, должны выполняться равенства:
a3 = j3; a2 = j2 + j3 и a1 = j1 + j2 + j3.
Эпюра углов закручивания показана на рис.2.
Пример 3.На балку (рис.3.1) на участке ВС действует распределенная нагрузка q=2 кН/м. Линейный размер a =2м. Допускаемое напряжение 
МПа.
Построить эпюры внутренних силовых факторов, определить диаметр балки из условия прочности по изгибающему моменту.
Рис.3.1
Решение:
1. Определяем реакции связей балки.
Строим расчетную схему (рис.3.2): заменяем действие связи А реакциями FAX,FAY,, действие связи В – реакцией FВУ,. Распределенную нагрузку q заменяем равнодействующей силой 
.
Рис.3.2
Уравнения равновесия балки 
Из уравнения 1) 
.
Из уравнения 3) 
.
Из уравнения 2)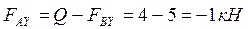 
.
2. Строим расчетную схему для определения внутренних силовых факторов: заданные внешние силы и реакции связей показываем в направлении их фактического действия (рис.3.3).
Согласно расчетной схеме на балку действуют силы, приложенные в сечениях А,В,С, следовательно балка имеет участки нагружения: АВ и ВС.
Рис.3.3
3. Определение внутренних силовых факторов и построение эпюр на участке ВС.
Проводим поперечное сечение 1-1 на произвольно выбранном расстоянии Х1 от сечения С, (). Строим расчетную схему «отсеченной» части балки, (рис.3.4): действие «оставшейся» части на «отсеченную» заменяем реакциями, действие распределенной нагрузки на «отсеченную» часть заменяем равнодействующей силой R=qX1.
Рис.3.4
Уравнения равновесия «отсеченной» части балки
Из уравнения 1) 
.
Из уравнения 2) 
Из уравнения 3) 
.
Значение силы Q1 зависитот координаты Х1 линейно - график прямая линия. Определим значение силы Q при двух значениях координаты Х1 и проведем прямую, проходящую через эти точки
Х1=0; 
;
Х1= a; 
.
Значение момента М1 имеет квадратичную зависимость от координаты Х1 – график изменения момента парабола. Для построения графика определим значение момента при двух значениях координаты Х1 и проведем параболу, проходящую через эти точки, обращенную выпуклостью против направления действия распределенной нагрузки
Х1=0; 
=0
Х1=a; 
