У данного микрометра на барабане С имеется шкала, содержащая 50 делений, а шаг винта b = 0,5 мм, поэтому точность микрометра
(4)
В данной работе при помощи микрометра необходимо измерить диаметр проволоки (или диаметр стержня). Значение диаметра можно найти по формуле:
(5)
Где 
- число наименьших делений шкалы
b – цена наименьшего деления шкалы
m = 50 – число всех делений на шкале барабана
n – номер того деления барабана, который в момент отсчёта совпадает с осью шкалы стебля D.
У данного микрометра цена деления линейной шкалы стебля b = 0,5 мм. Соседние верхние и нижние риски шкалы сдвинуты относительно друг друга на 0,5 мм, цифры поставлены только для делений нижней шкалы, т.е. нижняя шкала представляет собой обычную миллиметровую шкалу.
Пример 2. Так как в данной работе применяется микрометр, у которого b = 0,5 мм, m = 50, то формула (5) примет вид:
(6)
На рис. 2 отсчёт по микрометру показывает:
Так как толщина чёрточек на стебле D составляет несколько сотых долей миллиметра, то трудно определить, прошёл ли барабан данную чёрточку или нет. Когда барабан сдвинется от нуля шкалы на целое число оборотов, то он должен стать на какой-либо чёрточке основной шкалы, и на нём будет цифра 0 против основной линии стебля. Если же сделан немного неполный оборот, то на барабане будет цифра, близкая к 50, если же сделано немного больше целого оборота, то цифра на барабане будет близкая к нулю. Таким образом, если на барабане стоит число, близкое к нулю, то барабан прошёл данное деление, если на барабане стоит число, близкое к 50, то барабан ещё не прошёл данное деление.
Порядок выполнения работы
В данной работе определяются размеры цилиндра при помощи штангенциркуля. Вычисляется объём цилиндра, а также плотность вещества цилиндра.
Определяется диаметр проволоки при помощи микрометра и вычисляется площадь поперечного сечения проволоки.
1. Штангенциркулем измеряются внешний диаметр 
, внутренний диаметр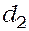 
, высота h цилиндра. Полученные данные записываются в таблицу 1.
2. Если масса цилиндра на нём не указана, то взвешиванием определяют его массу 
с точностью до 100 мг.
3. По формуле 
вычисляют объём цилиндра.
4. По формуле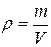 
вычисляют плотность материала цилиндра.
5. Микрометром не менее чем в 10 местах определяют диаметр d проволоки (или стержня). Вычисляют средний диаметр. Записывают полученные данные в таблицу 2.
6. Вычисляют площадь поперечного сечения проволоки. Полученные данные записывают в таблицу.
7. Вычисляют абсолютную и относительную погрешности при определении диаметра проволоки.
Таблица 1.
|
| d1 | d2 | h | V | r | |
| Един. Измер. | кг | мм | мм | мм | м3 | 
|
| Среднее |
Таблица 2.
| № | Средн. | ||||||||||
| d | |||||||||||
| Dd |
Контрольные вопросы
1. Что такое нониус? Объясните его устройство.
2. Что называется точностью нониуса. Напишите расчёт точности нониуса для данного штангенциркуля.
3. Сформулируйте правило измерения длины штангенциркулем.
4. Как устроен микрометр?
5. Чему равен шаг микрометрического винта для данного микрометра?
6. Как определить диаметр проволоки микрометром?
7. Как вычислить абсолютную погрешность измерения?
8. Как вычислить относительную погрешность?
9. Что такое плотность вещества?
10. Сколько кубических миллиметров содержится в одном кубическом метре?
Лабораторная работа № 1-02 (12)
ПРОВЕРКА ЗАКОНА ГУКА И ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ПРИ РАСТЯЖЕНИИ
Приборы и принадлежности: прибор для определения модуля Юнга, набор грузов, линейка.
Теория работы и описание приборов
Под влиянием внешних сил всякое твердое тело деформируется, т.е. изменяет свою форму. Упругой называется деформация, исчезающая с прекращением действия силы.
По закону Гука величина деформации Dх пропорциональна действующей силе F:
(1)
где С - постоянная величина для данной упругой деформации данного твердого тела.
Рассмотрим деформацию продольного растяжения.
Представим себе однородный стержень или проволоку длиной L с площадью поперечного сечения S, к концу которой приложена сила F. В результате действия приложенной силы длина стержня или проволоки изменится на величину ∆L – это абсолютная деформация. Величину деформации характеризуют также относительной деформацией стержня: 
. Для стержня поперечного сечения S под влиянием одной и той же силы относительная деформация e тем меньше, чем толще стержень, т.е. чем больше S.
Отсюда для упругой деформации растяжения получаем, что относительное изменение длины 
должно быть пропорционально
величине 
, т.е. силе, отнесенной к единице площади поперечного сечения стержня. Эту величину s= назовём напряжением. Тогда окончательно имеем:
(2)
|
где коэффициент a, носящий название коэффициента упругости,
зависит уже только от материала, из которого сделан стержень. В справочной литературе упругость материала характеризуют обратной величиной
, (3)
которую называют модулем продольной упругости, или модулем Юнга.
Вводя в (2) вместо коэффициента a модуль Юнга, получим
(4)
Откуда
(5)
или
(7)
Модуль Юнга характеризует упругие свойства материала при продольных деформациях и численно равен силе, удлиняющей стержень в два раза при его поперечном сечении, равном единице.
Прибор для определения модуля Юнга представляет собой массивную пластину А, на которой крепятся струна В, индикатор удлинения И и рычаг R, создающий растягивающее усилие. Схема прибора показана на рис. 3.
Рычаг имеет отношение плеч 
=10 или 5 и, таким образом, струну будет растягивать сила, равная 10×Р или 5Р, где Р - вес подвешенных на рычаг грузов.
Пружинный индикатор И соприкасается с рычагом в точке С. Цена деления индикатора 0,01 мм. Растяжение струны, создаваемое весом самого рычага, не учитывается и измеряется только дальнейшая деформация струны (рис.3).
Порядок выполнения работы
1. Вращением ободка устанавливают индикатор на нуль. Груз Р на рычаге при этом должен отсутствовать.
2. Измеряют при помощи линейки длину L той части струны В, удлинение которой измеряется индикатором (см. рис. 3).
3. Микрометром измеряют диаметр струны в разных местах и вычисляют площадь поперечного сечения S (по среднему значению диаметра).
4. Подвешивая на рычаг груз массой в 0,1 кг, отсчитывают удлинение по индикатору. Снимая и подвешивая груз вновь, опыт повторяют при той же нагрузке 3 раза и записывают в таблицу среднее значение удлинения для данного груза.
5. Добавляя грузы каждый раз по 0,1 кг, повторяют измерения по пункту 4, доводя нагрузку на рычаг до 0,6 кг.
6. Полученные данные заносят в таблицу.
7. Проводят вычисления и строят график зависимости напряжения 
от относительной деформации e.
Таблица
| №№ п/п | L | S | F | ∆L | 
| 
| Е | <Е> |
| Единицы измер. bbbbbbbbbbизмерений | м | м2 | Н | м | Па | – | Па | Па |
| 1. | ||||||||
| 2. | ||||||||
| 3. | ||||||||
| 4. | ||||||||
| 5. | ||||||||
| 6. |
Контрольные вопросы
1. Сформулируйте закон Гука и напишите его формулу.
2. Что называется модулемЮнга, напряжением, относительным удлинением?Какими формулами они выражаются?
3. От каких величин зависит модуль Юнга и какими единицами он измеряется в системе СИ?
Лабораторная работа № 1-03 (13)
ИЗУЧЕНИЕ ЗАВИСИМОСТИ ПЕРИОДА УПРУГИХ КОЛЕБАНИЙ ОТ МАССЫ
Приборы и принадлежности: пружина на кронштейне, набор грузов, секундомер.
Теория работы и описание приборов
При колебаниях тело совершает движения, периодически возвращаясь к положению равновесия. Время Т, в течение которого совершается одно полное колебание, называется периодом колебания. При простом гармоническом колебании смещение тела от положения равновесия у определяется уравнением
(1)
где А - амплитуда колебания - наибольшее смещение от положения равновесия, возможное для данного колебания;
w - круговая частота колебания;
t – время.
(2)
Скорость v при колебательном движении вычисляется, как первая производная смещения у по времени t:
или 
(3)
Ускорение а при колебательном движении определяется, как первая производная скорости v по времени t:
(4)
Сила, вызывающая колебание, периодически возвращает тело в положение равновесия и поэтому называется возвращающей силой. По второму закону динамики можно написать
или 
(5)
Если тело массой m совершает колебания на пружине, то в этом случае возвращающая сила определяется упругими свойствами пружины.
По закону упругих деформаций (закон Гука) упругая сила F прямо пропорциональна величине деформации (смещению) и имеет направление, противоположное смещению
(6)
где 
- коэффициент жесткости пружины.
Знак минус показывает, что сила 
по направлению противоположна смещению 
. Решая совместно уравнения (5) и (6), получаем: 
, откуда
(7)
Подставляя в формулу (7) значение wиз (2), получим:
(8)
откуда период упругих колебаний
(9)
Уравнение (9) можно записать в виде
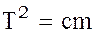(10)
где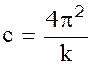 
- коэффициент пропорциональности (для определенной пружины величина постоянная).
Целью настоящей работы является:
1. Экспериментальная проверка зависимости периода упругих колебаний от массы и графическое выражение этой зависимости в координатах (m, 
).
2. Определение коэффициента жесткости пружины. Используемая в работе установка состоит из пружины, один конец которой жестко соединен с кронштейном (рис. 4). На конце пружины П имеется винт длянавинчивания грузов.
Под величиной массы колеблющегося тела 
в этой установке следует понимать не только массу навешенных грузов, но и массу m0 самой пружины, указываемую на установке.
Порядок выполнения работы
1. Навинтить на пружину по 8 грузов m, слегка оттянуть пружину и отпустить. Система придет в колебательное движение. По секундомеру определить время t, в течение которого происходит 10 или 20 полных колебаний системы. Из полученных данных определить период Т1 по формуле 
.
Не меняя груза, опыт повторить не менее трех раз и найти среднее значение Т1.
2. Снять с пружины один груз. Определить период Т2, как было описано выше.
3. Снимая каждый раз по одному грузу, определить периоды Тз. Т4 и т.д. Каждый опыт повторить не менеетрех раз и найти среднее значение периодов.
В таблицу записывается масса m всех грузов m1. Масса каждого груза указана на нем.
4. Из формулы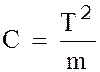 
найти коэффициент пропорциональности пружины С для всех найденных значений mi + m0, и соответствующих им значений Т. Определить среднее значение С.
5. Построить график зависимости Т2 от (mi+m0)=m.
| Таблица наблюдений | ||||||||
| №№ наблюдений | m0 | m1 | m | n | t | T | T2 | C |
| Единица измерения | кг | кг | кг | кол. | с | с | c2 | c2 /кг |
Контрольные вопросы
1. Какие колебания называются гармоническими? Что такое период колебания, амплитуда?
2. Напишите формулы скорости, ускорения и возвращающей силы при гармоническом колебательном движении, как они получаются?
2. Сделайте вывод формулы для коэффициента жесткости пружины.
Лабораторная работа № 1-04 (14)
ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ СЫПУЧИХ ТЕЛ
ВОЛЮМОМЕТРОМ ЛЕРМАНТОВА
Приборы и принадлежности: волюмометр Лермантова, сосуд с зерном, весы, разновес.
Теория работы и описание приборов
Плотность (r) численно равна отношению массы тела (вещества) к его объему.
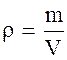
Для определения плотности зерна необходимо определить его массу и объем.
Масса тела численно равна его весу, поэтому массу зерна можно определить взвешиванием. Объем же зерна (V), как сыпучего тела, найдем как разность между внутренним объемом сосуда (V1), в который засыпано зерно, и объемом воздуха (V2), находящегося в этом сосуде между зернами и над ними.
Для определения объема сыпучих тел пользуются методом, основанном на изотермическом законе газового состояния (законе Бойля-Мариотта) с использованием прибора волюмометра, сконструированного Лермантовым (рис. 5).
Волюмометр состоит из толстостенного стального сосуда А с резьбой на конце. Этот сосуд навинчивается от руки на чугунную крышку В, от которой отходит стеклянная трубка С, имеющая расширение в виде шарика Д.
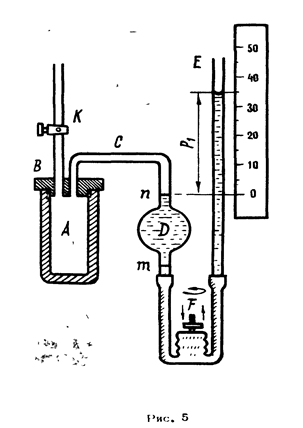
Объем шарика V0, ограниченный метками m и n, известен, и указан на приборе.
Шарик Д соединяется резиновой трубкой, наполненном водой, со стеклянной трубкой Е. Таким образом, трубка Е и трубка С образуют манометр. Сосуд А сообщается с внешним воздухом с помощью крана К.
Открыв его, можно установить воду в обоих коленах манометра на одинаковом уровне m, так как давление на поверхность воды в обоих коленах станет равным атмосферному.
Определение объема сыпучих тел (зерна) состоит из следующих двух операций: 1) определяют объем воздуха V1, заполняющего сосуд А и часть трубки С до метки n; 2) затем в сосуд А закладывается навеска зерна и определяется объем воздуха, заполняющего не занятую зерном часть сосуда А, промежутки между зернами и трубку С до метки n. Назовем этот объем V2. Очевидно, объем зерна V будет равняться разности этих объемов:
V = V1 – V2. Для определения V1 и V2 составляются уравнения на основе закона Бойля-Мариотта.
В том и в другом случаях искомый объем рассчитывается по закону изотермического процесса. Для этого объем V1 +V0 сперва берется при атмосферном давлении р, а затем поднятием воды в колене Е тонометра изотермически сжимается до объема V1, который, очевидно, будет соответствовать давлению p + p1, где
р - показание манометра.
Применяя закон изотермического процесса – закон Бойля-Мариотта, можем написать:
раскрыв скобки, получим
или 
откуда 
Затем в сосуд А закладывается навеска зерна и проделывается то же, что и в предыдущею случае. Применяя закон изотермического процесса, получим:
откуда: 
,
где 
- объем оставшегося воздуха в сосуде А и трубке С до уровня n;
- показание манометра.
Искомый объем зерна 
.
Откуда объем зерна 
.
Подставляя это выражение V в формулу плотности, 
получим расчётную формулу для определения плотности
(1)
Описанное выше определение объема производилось способом сжатия воздуха в сосуде А.
То же определение можно было бы сделать способом расширения. Последняя формула показывает, что для решения задачи необходимо определить показания манометра 
и .
Порядок выполнения работы
1. Открыть кран К. При помощи винта F установить воду в колене C против метки m.
2. Закрыть кран К. Проверить герметичность навинчивания сосуда А. Винтом p установить уровень воды в колене С против метки n, заполнив шарик D.
3. Определить по шкале высоту уровня воды в колене Е, считая от уровня n в колене С. Это и будет показанием манометра р1.
4. Операции пунктов 1, 2, 3 проделать не менее трех раз и столько же раз рассчитать p1.
5. Открыть кран К, снять сосуд А, всыпать в него на 3/4 объема зерно, сосуд А навинтить на прежнее место, проделать операции, описанные в пунктах 1, 2, 3. Будет найдено показание манометра p2. Эту величину определить столько же раз, как и величину р1.
6. Взвешиванием на весах определить массу зерна в цилиндре.
7. Определить по барометру атмосферное давление р, (поправку на температуру не производить) и все найденные величины занести в таблицу.
8. Пользуясь выведенной формулой (1), вычислить плотность зерна.
9. Результаты измерений и вычислений занести в таблицу.
Таблица наблюдений
| №№ наблюдений | p | V0 | р1 | р2 | m | r |
| Ед. измерения | Па | м3 | Па | Па | кг | кг/м3 |
| Средние значения |
Указания к работе
1. Объем шарика V0 указан на приборе.
2. 1 мм рт. ст. = 133 Па
3. 1 мм вод.ст. = 9,81 Па
Контрольные вопросы
1. Что называется плотностью вещества и в каких единицах она измеряется в системе СИ?
2. В чём состоит трудность определения объема сыпучих тел и как она определяется в данной работе?
3. Сделайте вывод расчётной формулы.
4. Сформулируйте закон изотермического процесса и напишите его формулу.
Лабораторная работа № 1-05 (15)
ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Приборы и принадлежности: прибор Обербека, маховик, грузы различной массы, штангенциркуль, масштабная линейка, секундомер, технические весы.
Теория работы и описание приборов:
Если к телу, которое может вращаться вокруг неподвижной оси, приложить вращающий момент М, то под действием этого момента изменится угловая скорость вращения тела w. Тело будет двигаться с угловым ускорением e.
Вращающий момент и угловое ускорение связаны вторым законом Ньютона для вращательного движения.
(1)
где 
– момент инерции тела относительно рассматриваемой оси вращения.
Момент инерции твердого тела равен сумме моментов инерции материальных точек 
.
(2)
Моментом инерции материальной точки называется физическая величина, характеризующая инертность точки к изменению ею угловой скорости под действием приложенного момента силы и измеряемая произведением массы точки на квадрат ее расстояния от оси вращения. Момент инерции тела зависит от распределения массы относительно заданной оси вращения и, следовательно, изменение расстояния отдельных частей вращающегося тела от оси вращения приводит к изменению момента инерции тела относительно этой оси.
Из формулы (1) можно определить момент инерции тела, если из опыта будут найдены момент силы и угловое ускорение
(3)
Для определения момента силы и углового ускорения опытным путем можно пользоваться одним из приборов, схемы которых приведены на рис. 6 и 7.
Прибор (рис. 6) состоит из шкива А, закрепленного на оси О. На шкиве укреплены четыре стержня, расположенных под углом 90° друг к другу. На стержнях помещены четыре цилиндрических тела с одинаковыми массами m. Эти тела могут перемещаться вдоль стержней и закрепляться на них в любом положении. Тела необходимо закреплять симметрично, т.е. так, чтобы их общий центр тяжести совпадал с осью вращения.
 |
Рис. 6
Груз m1, соединенный со шкивом нитью, падая вниз, приводит во вращение прибор. На тело m1 действуют две силы: сила тяжести Р направленная вниз, и сила натяжения нити Fн, направленная вверх. Следовательно, результирующая сила F, под действием которой тело m1 движется вниз, равна разности указанных сил, т.е.
(4)
Отсюда
(4a)
или, т.к. 
, то
(4б)
где g – ускорение силы тяжести, a – ускорение поступательного движения тепа m1.
Сила натяжения нити Fн создает вращающий момент и сообщает телу угловое ускорение e. Момент силы Fн будет
(5)
где r – радиус шкива.
Угловое ускорение e связано с ускорением поступательного движения тела m1 формулой
(6)
Поступательное движение тела m1 является равноускоренным, без начальной скорости и его ускорение a можно вычислить по формуле:
(7)
где h – высота, на которую опустилось тело m1 за время t. Из формул (3) и (5) получим для J:
(8)
Подставляя в формулу (6) a из формулы (7), получим выражение для e:
(8a)
Подставляя e и a в (8) для J окончательно получим:
(8б)
Формула (8б) и является рабочей формулой для определения момента инерции опытным путем.
Упражнение 1
Пусть J0 – момент инерции крестовины без цилиндрических тел, а J1, и J2 – моменты инерции крестовины для случаев, когда четыре цилиндрических тела закреплены на стержнях на расстоянии от оси R1 и R2, соответственно (R2>R1).
Момент инерции системы тел равен сумме моментов инерции отдельных тел, на основании формулы (2) можно написать
(9)
Итак, применяя эту формулу к нашему случаю, получим:
(9а)
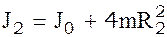(9б)
Деля почленно уравнение (9б) на (9а), получим:
(9в)
В данной лабораторной работе теоретически полученная формула (9в) проверяется на опыте.
Порядок выполнения работы
1. Подвижные тела m закрепляются на стержнях как можно ближе к оси вращения, но так, чтобы крестовина была в безразличном равновесии.
2. Измеряется штангенциркулем диаметр шкива (2r).
3. На технических весах с точностью до 0,5 г определяется масса тела m1.
4. Нить, на конце которой прикреплено тело m1. наматывается на шкив так, чтобы тело было на высоте h над уровнем пола. Высота h измеряется масштабной линейкой, укрепленной на стене.
5. Предоставив возможность телу m1 падать, по секундомеру определяют время его падения. Секундомер включают в момент начала падения тела и останавливают одновременно с ударом тела о пол.
6. Аналогичные опыты проводятся также при расположении грузов на концах стержней и со снятыми грузами m. Для каждого из трех случаев проводят не менее трех опытов, по формуле 8б вычисляют момент инерции J и далее J среднее.
7. Упрощенно по способу прямых измерений вычисляют абсолютную и относительную погрешности. Затем, воспользовавшись средними значениями J, проверяют справедливость формулы (9в), вычислив отдельно 
и 
и делают письменный вывод о справедливости формулы (9в).
Результаты вычислений и измерений заносят в таблицу.
Таблица наблюдений
| №№ наблюдений | 
| 
| 
| 
|
| 
|
| единицы измерения | кг | м | м | с | Кг×Н/м2 | Кг×Н/м2 |
| Цилиндрические грузы у шкива | ||||||
| Цилиндрические грузы на концах стержней | ||||||
| Крестовина без грузов | ||||||
 |
Упражнение 2 Для выполнения второго упражнения используется прибор, схема которого приведена на рис. 7.
Этот прибор представляет собой массивный металлический диск А (маховик), неподвижно закрепленный на валу В. Вал может вращаться с малым трением в подшипниках вокруг горизонтальной оси 00. Ось вращения проходит через центр тяжести маховика. На валу маховика плотно насажен шкив радиуса r, на который в несколько оборотов наматывается нить. Прибор приводится во вращательное движение силой натяжения с грузом m1. Рабочая формула (8б), полученная для крестовин, справедлива и для данного случая.
Из рассмотренной теории вытекает, что при различных массах m1, прикрепленных к свободному концу нити, момент инерции маховика должен оставаться неизменным. Проверка этого вывода и является целью настоящей работы.
Порядок выполнения работы
1. Измеряется штангенциркулем диаметр (d=2r) шкива.
2. На технических весах определяют величину масс m1 и m2 (с точностью до 0,5r).
3. Наматывают на шкив нить, на конце которой прикреплено тело m1 или m2 поднимая их на высоту h над уровнем пола.
4. Предоставив телу возможность падать, по секундомеру определяют время падения.
5. Опыты повторяют не менее пяти раз с каждым из двух тел m1 и m2. Данные опыта записывают в таблицу наблюдений.
Таблица наблюдений
| Измерения с первым грузом | ||||||
| №№ наблюдений |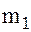 
|
|
|
| 
| 
|
| единицы измерения | кг | м | м | с | 
|
|
| Измерения со вторым грузом | ||||||
| №№ наблюдений | 
|
|
|
| 
| 
|
| единицы измерения | кг | м | м | с |
|
|
Контрольные вопросы
1. Что называется угловой скоростью и угловым ускорением?
2. Как связаны угловая скорость и угловое ускорение с аналогичными величинами при поступательном движении? Сделайте вывод формул этой зависимости.
3. Сформулируйте второй закон Ньютона для вращательного движения.
4. Что называется моментом силы?
5. Что называется моментом инерции точки, тела?
6. Дайте вывод рабочей формулы (8в).
7. Что называется абсолютной и относительной ошибками, и как они вычисляются?
Лабораторная работа № 1-06 (16)
ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТЕЛА ПИКНОМЕТРОМ И ГИДРОСТАТИЧЕСКИМ ВЗВЕШИВАНИЕМ
