Задание 2.1.
1. При расчете воздушного стального провода получили уравнение для определения усилия натяжения при гололеде F3 + 443 F 2 – 94,1∙105 = 0. Найти положительный корень (усилие натяжения).
2. При решении вопроса об излучении абсолютно черного тела встречается уравнение 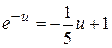 . Решить его.
. Решить его.
3. Решить уравнение 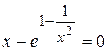 , которое встречается в задаче о наивыгоднейшей конструкции изоляции для труб.
, которое встречается в задаче о наивыгоднейшей конструкции изоляции для труб.
4. Решить уравнение ln (u) = α+βum, m ˃ 0, встречающееся в электротехнике.
5. Наибольшая скорость воды в трубе круглого сечения достигается тогда, когда центральный угол удовлетворяет уравнению tg (x) = x. Определить этот угол.
6. В задаче о распределении тепла в стержне встречается уравнение tg (x) +γx = 0. Решить его.
7. При исследовании беспроволочного излучателя получено уравнение x tg(x) = c, c = const. Для какого наименьшего положительного или отрицательного значения х постоянная равна 1.
8. Решить уравнение 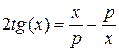 , которое встречается при решении задачи о распространении тепла в стержне при наличии лучеиспускания в окружающее пространство.
, которое встречается при решении задачи о распространении тепла в стержне при наличии лучеиспускания в окружающее пространство.
9. При определении критической нагрузки для балки, свободно опирающейся одним концом, закрепленной другим и сжимаемой продольной силой, встречается уравнение 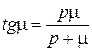 . Решить его при
. Решить его при
р = 2, полагая, что μ = π + х.
10. Площадь кругового сегмента, дуга которого α, определяется формулой 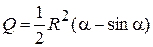 (α есть радианная мера дуги). Найти сегмент, площадь которого равна 1/5 площади круга (найти сегмент – значит, найти угловую меру его дуги).
(α есть радианная мера дуги). Найти сегмент, площадь которого равна 1/5 площади круга (найти сегмент – значит, найти угловую меру его дуги).
11. Прямоугольная стальная пластинка размерами 150 ˣ 100 см и толщиной 0,5 см защемлена по краям и подвергается действию равномерно распределенной нагрузки, равной 0,25 кг/см2. Стрела прогиба z определяется из уравнения 1,05 z 3 + 0,70 z = 96,4. Найти z, решив данное уравнение(найти корень с четырьмя значащими цифрами).
12. Шар радиуса R разделить на m частей, равных по объему, путем проведения плоскостей, параллельных между собой (m = 5; m = 10). Отношение 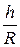 найти с пятью верными десятичными знаками (h – высота шарового слоя).
найти с пятью верными десятичными знаками (h – высота шарового слоя).
13. Найти корень уравнения 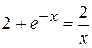 с точностью до трех десятичных знаков (уравнения такого типа встречаются при изучении колебаний стержня под действием продольного удара).
с точностью до трех десятичных знаков (уравнения такого типа встречаются при изучении колебаний стержня под действием продольного удара).
14. Найти наименьший положительный корень уравнения tg(x) = – 0,6 x с тремя верными десятичными знаками (уравнение встречается при изучении теплового режима в стенке).
15. Найти наименьший положительный корень уравнения 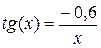 с тремя верными десятичными знаками.
с тремя верными десятичными знаками.
Задание 2.2.
Решить уравнения, приведенные в табл. 2.1.
Таблица 2.1. Варианты заданий для самостоятельного решения
| № | Уравнение | № | Уравнение |
| 3 х 4 + 4 х 3 – 12 х 2 – 5 = 0 | x – sin x = 0,35 | ||
| 0,5 х + 1 = (х – 2)2 | 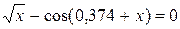
| ||
| (х – 4)2 log0,5 (x – 3) = –1 | sin (0,5 + x) = 2 x – 0,5 | ||
| x 2 cos(2 x) = –1 | ln x + (x +1)3 = 0 | ||
| (x – 2)2 2 x = 1 | 3 x – 2 ex = 1 | ||
| ((x – 2)2 – 1)2 x = 1 | 2 sin (x – 0,6) = 1,5 – x | ||
| (x – 2) cos x = 1, – 2π ≤ x ≥ 2π | 5 x – 8ln x = 8 | ||
| (x – 2)3 lg(x + 11) = 1 | x = 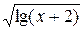
| ||
| 5sin x = x – 1 | 1,8 x 2 – sin10 x = 0 | ||
| x 4 ∙3 x = 2 | ctg(1,05 + x) – x 2 = 0 | ||
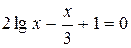
| ctg x – 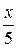 = 1 = 1
| ||
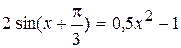
| 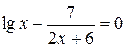
| ||
| 2 x 2 – 0,5 x – 3 = 0 | x 3 + 0,1 x 2 + 0,4 x – 1,2 = 0 | ||
| cos(x + 0,5) = x 3 | 0,5 x + lg(x – 1) = 0,5 | ||
| 2 ex = 5 x + 2 | sin0,5 x + 1 = x 2 | ||
| sin(x – 0,5) – x + 0,8 = 0 | 2 x + lg x = – 0,5 | ||
tg3 x = x – 1, – 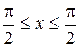
| 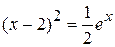
| ||
| arctg(x – 1) + 2 x = 0 | x = 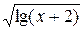 +6 +6
| ||
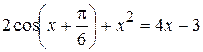
| 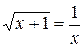
| ||
| x 2 – 5 + 0,42 x = 0 | x 2 + 4sin x = 0 |
Лабораторная работа №3






