Работа магнитного пола по перемещению проводника о током

 

На проводник с током в магнитной пола действует сила Ампера, под действием которой он перемещается. Вычислим работу, совершаемую такими силами при перемещении проводника.

Пусть отрезок проводника Δl c током перемещается в магнитном поле с индукцией В на расстояние Δх (Рис.21.6). Вектор В можно разложить на 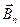и . Т.к. сила Ампера всегда перпендикулярна полю, тo сос­тавляющая вызывет силу, пер­пендикулярную перемещению Δх, и работа этой составляющей будет равна нулю. Поэтому

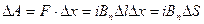
где ΔS - площадь, описываемая при движении проводника. Окончательно

 

(21.16)

 

Закон полного тока

 

Поскольку магнитные силовые линии являются замкнутыми, то соотношение между током и вызванным им магнитный полем характеризуют не потоком магнитной индукции, а циркуляцией вектора магнитной индукции вдоль замкнутой кривой. Для простоты рассмотрим магнитное поле бесконечного прямолинейного про­водника с током (Рис. 21.7). Линии магнитной индукции в этом случае являются концентрическими окружностями, лежащими в плоскос­ти, перпендикулярной току. В этом случае циркуляция равна. Т.к. b во всех точках направлен по касательной, тo α=0, а :

(21.17)

Этот результат справедлив для любого произвольного контуpa, который охватывает токи. Если внутри контура имеется несколько токов, то

(21.18)

формулы (21.17) и (21.18) выражают закон полного тока или теорему о циркуляции вектора В.

Для магнитного поля циркуляция вектора магнитной индук­ции вдоль замкнутого контура равна произведению μ₀ на алгеб­раическую сумму токов, охватываемых этим контуром.

Эта теорема выражает один из основных законов магнетизма. Сопоставляя этот результат с условием потенциальности электро­статического поля - формула (14.2), видно также, что магнитное поле не является потенциальным. Такие поля называют вихревыми.

Применим формулу (21.17) для вычисления индукции магнит­ного поля на оси тонкого соленоида - систему круговых токов, диаметр которых много меньше длины (Рис. 21.8). Индукция внутри такого соленоида направлена вдоль его оси. Применяя (21.17) к прямоугольному контуру 1-2-3-4, имеем

(21.19)

Т.к. поле сосредоточено внутри соленоида, а на участках 1-2 и 3-4 В перпендикулярен участкам контура и , то из (21.19) получаем

где l - длина соленоида, N- число витков соленоида.

Итак,

(21.20)

где n - число витков, приходящихся на единицу длины.

 

Лекция 30	Явление и закон электромагнитной индукции – его выводы на основе закона сохранения энергии и электронной теории.
	Самоиндукция и индуктивность. Взаимная индукция. Объёмная плотность энергии магнитного поля.