НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА.Ψ – ФУНКЦИЯ
1. Что такое фотоэффект? Каковы законы фотоэффекта? Формула фотоэффекта. Использование фотоэффекта.
2. В чем заключается эффект Комптона?
3. Двуличность света, волны или частицы?
4. Электрон как частица и волна.
5. Попадание микрочастиц на неопределенность Гейзенберга. Неопределнность координат и импульса, неопределенность энергии и времени.
6. Что такое волновая функция и ее свойства?
Задачи
1. Определить красную границу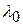 
фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны 
нм максимальная скорость фотоэлектронов равна 3,65Мм/с
2. На металлическую пластину направлен пучок ультрафиолетовых лучей (
мкм). Фототок прекращается при минимальной задерживающей разности потенциалов 
В. Определить работу выхода электронов из металла.
3. Калий (работа выхода 
эВ) освещается монохроматическим светом с длиной волны 
нм. Определить возможную кинетическую энергию фотоэлектрона.
4. При фотоэффекте с платиновой поверхности (
эВ) задерживающий потенциал оказался равным 
В. Найти длину волны применяемого облучения; максимальную длину волны, при которой еще возможен фотоэффект.
5. На фотоэлемент с катодом из рубидия (
эВ) падают лучи с длиной волны 
нм. Найти наименьшее значение задерживающей разности потенциалов, которую нужно приложить к фотоэлементу, чтобы прекратить фототок.
6. Фотон с энергией 
кэВ рассеялся под углом 
на первоначально покоившемся свободном электроне. Определить энергию рассеянного фотона.
7. При эффекте Комптона энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния равен 
. Найти энергию и импульс рассеянного фотона.
8. Определить угол 
, на который был рассеян 
квант с энергией 
МэВ при эффекте Комптона, если кинетическая энергия электрона отдачи 
МэВ.
9. Излучение возбужденного атома происходит в течение времени 
нс, длина излучения 
нм. Оценить, с какой наибольшей точностью 
может быть определена энергия излучения.
10. Атом испустил фотон с длиной волны 
нм. Продолжительность излучения 
с. Какова минимальная неопределенность 
, с которой может быть измерена длина волны излучения?
Глава 34. УРАВНЕНИЕ ШРЕДИНГЕРА. ПОТЕНЦИАЛЬНАЯ ЯМА
1. Каков вид уравнения Шрёдингера? Его суть?
2. Каков вид стационарного уравнения Шрёдингера? Суть его толкования.
3. Его решение для потенциальной ямы.
Задачи
1. Частица в потенциальном ящике шириной 
находится в основном состоянии. Определить, в каких точках интервала 
плотность вероятности нахождения частицы максимальна и минимальна.
2. Частица в потенциальном ящике находится в основном состоянии. Какова вероятность нахождения частицы в крайней трети ящика?
3. Частица в бесконечно глубоком одномерном прямоугольном ящике шириной находится в возбужденном состоянии (
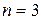). Определить, в каких точках интервала плотность вероятности нахождения частицы имеет максимальное и минимальное значения.
4. Частица в одномерном потенциальном ящике с абсолютно непроницаемыми стенками шириной 
нм находится в основном состоянии. Какова вероятность обнаружения частицы в крайней трети ящика?
5. Частица в одномерном потенциальном ящике с абсолютно непроницаемыми стенками шириной находится в возбужденном состоянии (
). Определить, в каких точках интервала плотность вероятности нахождения частицы максимальна и минимальна.
6. Электрон находится в одномерной прямоугольной потенциальной яме ширины с бесконечно высокими стенками. В каких точках интервала плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить значение плотности вероятности для этих точек.
7. В одномерной прямоугольной потенциальной яме ширины с бесконечно высокими стенками движется электрон. Вычислить вероятность обнаружения электрона на первом энергетическом уровне в интервале 
.
8. Частица в одномерном потенциальном ящике с абсолютно непроницаемыми стенками шириной находится в низшем возбужденном состоянии. Вычислить вероятность нахождения частицы в интервале 
.
9. Вычислить отношение вероятностей нахождения электрона на первом и втором энергетических уровнях в интервале 1/4, равноудаленном от стенок одномерной потенциальной ямы шириной .
