1. В каком случае используется векторное сложение?
2. Каков результат, когда складываются колебания с близкими частотами?
3. В каком случае возникает амплитудная модуляция?
4. Что происходит, кода складываются взаимно ортогональные колебания?
5. В каком случае возникают фигуры Лиссажу?
Задачи
1. Найдите амплитуду и начальную фазу гармонического колебания, полученного в результате векторного сложения колебаний: 
и 
,м. Отв. 0,46м; 62,5
2. В результате сложения двух гармонических колебаний с одинаковым периодом и одинаковой амплитудой, результирующее колебание оказывается с той же амплитудой. Найти разность фаз складываемых колебаний. Отв. 1200
3. Складываются колебания: 
м и 
, м найдите результирующее. Отв. 0,4cos2t۰cos38t, м
4. Складываются колебания: 
м и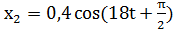 
, м найдите результирующее. Отв. 0,5cos(18t+ 530), м
5. Точка участвует в двух взаимно-перпендикулярных колебаниях х=cosπt и у=cos(π/2)t. Найдите траекторию результирующего движения. Отв. 2у2 –х=1
Глава 21. СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛА. АМПЛИТУДНАЯ МОДУЛЯЦИЯ. ФУРЬЕ-АНАЛИЗ И СИНТЕЗ
1. Что такое спектр сигнала? Как образуется спектр амплитудно-модулированного сигнала?
2. В каком случае применяется теорема Фурье? В чем она заключается?
3. Как определяются члены ряда Фурье, коэффициенты ряда?
4. Как определяется оптимальное число гармоник ряда?
5. Что называют Фурье-анализом и Фурье синтезом?
Задачи
1.Сигнал описывается функцией х=0,4(1+ 0,4(cos2t+0,6cos4t))۰cos2000t, м. Найдите амплитуды спектральных составляющих. Отв. 0,4м; 0,08м; 0,048.
|
2. Используя сигнал задачи 1, определите частотный состав. Отв.318,15Гц, 318,47Гц, 318,79Гц; 319,11Гц; 317,83Гц
3. На рис. 6 задан периодический сигнал
с периодом 0,08с и амплитудой 0,5В.
Найдите 8 первых гармоник ряда Фурье.
Отв. х(t)= 0,637 cosωt + 0,212 cos3ωt +0,127 cos5ωt +0,091 cos7ωt +0,071 cos9ωt + 0,058 cos11ωt + 0,049 cos13ωt + 0,042 cos15ωt
4.Используя условия и результат задачи 6, укажите, сколько гармоник следует оставить, если отбросить все гармоники, амплитуда которых менее 1/10 основной. Отв. 5.
5. Используя условия и результат задачи 6, укажите, сколько гармоник следует оставить, если рассматривать энергетический вклад в сигнал (90%). Отв. 3.
Глава 22. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС. ПРИМЕНЕНИЕ РЕЗОНАНСА В ИНЖЕНЕРНОЙ ПРАКТИКЕ
1. Какие колебания считаются вынужденными? Каково в этом случае дифференциальное уравнение колебательной системы?
2. Решение дифференциального уравнения в виде свободной и принужденной составляющих?
3. Что такое логарифмический декремент затухания?
4. АЧХ и ФЧХ принужденной составляющей.
5. Каковы условия резонанса. К чему ведет резонанс в электрических и механических колебательных системах?
Задачи
1. Пружинный маятник массой 0,25кг имеет коэффициент упругости 25Н/м и колеблется с амплитудой 0,2м в условиях вязкого трения с коэффициентом 0,2кг/с. В момент времени, когда начальная фаза равна нулю, начинает действовать вынуждающая сила по закону 10 cos8t, Н. Составьте дифференциальное уравнение вынужденного колебания. Отв. 
2. Используя условия задачи 1, найдите свободную составляющую. Отв. хсв= 0,2е -0,4t cos10t, м
3. Используя ответ задачи 3, определите логарифмический декремент затухания. Отв. 0,25
4. Используя условия задачи 1, найдите время релаксации. Отв. 1,6с
5. Используя условия задачи 1, определите добротность колебательной системы. Отв. 12,56
6. Используя условия задачи 1, найдите принужденную составляющую. Отв. хпр= 0,14 cos(8t – 10,20)
7. Используя условия задачи 1, определите амплитуду принужденной составляющей, если циклическая частота вынуждающего источника станет равной 10рад/с. Отв 0,78м
8. Используя условия задачи 1, найдите величину коэффициента вязкого трения, при котором система перестает быть периодической? Отв. >5кг/c
9. Дифференциальное уравнение последовательного колебательного контура 
найдите амплитуду принуждающего тока в контуре, если активное сопротивление 10 Ом. Отв.20А.
10. Используя условия задачи 9, определите индуктивность, и емкость контура. Отв. 40мГн; 25мкФ.
