Первичная обработка данных

ПРИМЕР ВЫПОЛНЕНИЯ ЛАБОРАТОРНЫХ РАБОТ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ

Лабораторная работа № 1

ПЕРВИЧНАЯ ОБРАБОТКА ДАННЫХ

При проведении экспериментов фиксировались значения случайной величины X, характеризующей время простоя оборудования в ожидании ремонта (в часах).

Задание: произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины Х.

1) Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания признака) и произведем расчеты, необходимые для вычисления числовых характеристик.

 

Таблица 1 – Расчетная таблица

Номер п/п	Выборка, час.	Вариацион-ный ряд, , час.
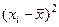
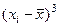
	6,72	0,21	-5,068	25,684	-130,163	659,6524
	8,2	0,4	-4,885	23,864	-116,58	569,5061
	0,4	0,64	-4,642	21,55	-100,036	464,3845
	12,9	0,69	-4,595	21,118	-97,0476	445,9774
	3,15	0,77	-4,509	20,33	-91,6644	413,3022
	34,5	0,93	-4,346	18,892	-82,1113	356,8922
	4,71	1,14	-4,142	17,158	-71,0714	294,3925
	1,14	1,51	-3,772	14,226	-53,6592	202,3917
	2,87	1,73	-3,55	12,601	-44,7323	158,7918
	3,07	1,86	-3,422	11,709	-40,0658	137,0981
	5,86		-3,277	10,741	-35,2003	115,3619
	11,4	2,1	-3,179	10,105	-32,1227	102,1135
	3,12	2,32	-2,964	8,7873	-26,0485	77,21641
	0,21	2,32	-2,961	8,7695	-25,9695	76,9043
	1,51	2,4	-2,885	8,3222	-24,0079	69,25838
	2,76	2,76	-2,521	6,3562	-16,025	40,40161
	0,93	2,87	-2,414	5,8281	-14,0699	33,96675
	2,4	2,87	-2,409	5,8055	-13,988	33,70356
	3,5	2,99	-2,294	5,2642	-12,0781	27,71187
	5,29	3,07	-2,214	4,9038	-10,8593	24,0474
	1,86	3,12	-2,163	4,6803	-10,1253	21,90503
	4,99	3,15	-2,132	4,5437	-9,68547	20,6456
	8,77	3,5	-1,776	3,1546	-5,60301	9,951645
	1,73	3,6	-1,683	2,8313	-4,76407	8,016242
	0,77	4,59	-0,691	0,477	-0,32948	0,227561
	5,99	4,61	-0,669	0,4478	-0,29968	0,200545
	7,95	4,71	-0,568	0,323	-0,18359	0,104347
	2,87	4,99	-0,292	0,0854	-0,02497	0,007299
	0,64	5,29	0,006	0,000036	0,0000002	1,66
	5,74	5,74	0,459	0,2103	0,096434	0,044222
	0,69	5,86	0,582	0,3384	0,196888	0,11454
	2,99	5,99	0,707	0,5003	0,35391	0,250336
	4,59	6,72	1,439	2,0704	2,978986	4,286387
	2,32	7,95	2,671	7,1361	19,06293	50,92364
	2,32	8,2	2,924	8,55	25,00068	73,10309
		8,77	3,492	12,193	42,57744	148,6755
	2,1	11,4	6,097	37,173	226,6467	1381,866
	4,61	12,9	7,608	57,874	440,2776	3349,414
	30,1	30,1	24,78	614,27	15224,23	377323,6
	3,6	34,5	29,26	855,97	25043,19	732688,6
Итого				1874,8	39956,09

 

2) Найдем размах выборки = 34,5- 0,21 = 34,29.

3) Длина интервала = = = 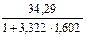5,424.

4) границы интервалов: = 0,21, =0,21+5,424 = 5,634, 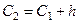= 5,634 +5,424 = 11,058,

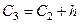= 11,058 +5,424= 16,482, = 16,482+ 5,424= 21,906, = 21,906+ 5,424 = 27,33,

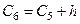= 27,33+ 5,424 = 32,754, = 32,754+ 5,424 = 38,178 .

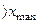5) Построим интервальный статистический ряд:

Таблица 2 – Интервальный статистический ряд

Границы интервалов 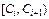, час.	Частоты	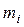Частости	Накопленные частости
[0.21; 5,634)		29/40	29/40
[5,634; 11,058)		7/40	36/40
[11,058; 16,482)		2/40	38/40
[16,482; 21,906)		0/40	38/40
[21,906; 27,33)		0/40	38/40
[27,33; 32,754)		1/40	39/40
[32,754; 38,178)		1/40
Итого

 

6) Вычислим числовые характеристики.

В качестве оценки математического ожидания используется среднее арифметическое наблюденных значений. Эта статистика называется выборочным средним.

.

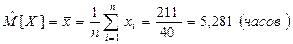Для оценивания по выборочным данным моды распределения, используется то значение сгруппированного статистического ряда 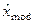, которому соответствует наибольшее значение частоты. По интервальному статистическому ряду определяется модальный интервал, в который попало наибольшее число элементов выборки, и в качестве точечной оценки моды может использоваться среднее значение этого интервала.

.

 

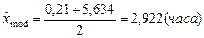Для определения выборочного значения медианы используется вариационный ряд. В качестве оценки медианы принимают средний (т. е. 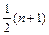-й) член этого ряда, если значение n – нечётно и среднее арифметическое между двумя средними (т. е. между -м и -м) членами этого ряда, если n – чётно. В нашем случае объем выборки 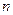= 40 - четное, т.е. в качестве оценки медианы примем

= .

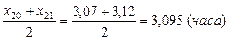В качестве оценки дисперсии используется статистика = .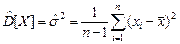

 

Оценка среднего квадратического отклонения = .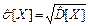

 

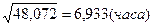Оценка коэффициента вариации .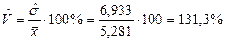

Оценка коэффициента асимметрии

.

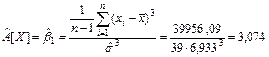Оценка коэффициента эксцесса

.

7) Для приближённого построения эмпирической функции распределения воспользуемся соотношением:

 

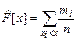
8) Построим гистограмму частот и эмпирическую функцию распределения.

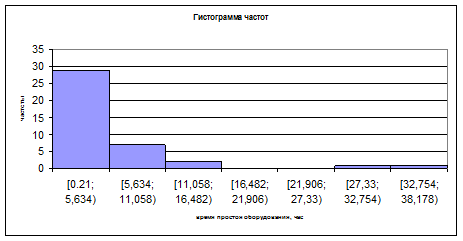
Рисунок 1 – Гистограмма частот

 

 

 

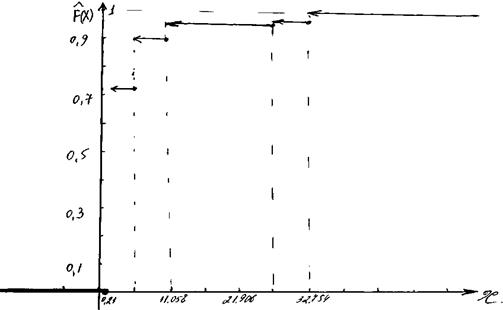
Рисунок 2 – Функция распределения

 

Вывод. В результате исследования выборки значений непрерывной случайной величины, характеризующей время простоя оборудования в ожидании ремонта, получили следующие результаты, час: минимальное время простоя – 0,21, максимальное – 34,54, среднее значение времени простоя оборудования – 5,28, наиболее вероятное время простоя оборудования – 2,922, средневероятное – 3,095, среднеквадратическое отклонение времени простоя оборудования от среднего значения составило 6,933. Оценка коэффициента вариации составила 131,3%, что указывает на большую колеблемость признака относительно среднего значения, оценка коэффициента асимметрии составила 3,074, оценка коэффициента эксцесса составила 9,423.

 

Лабораторная работа № 2

Подбор закона распределения
одномерной случайной величины

Цель работы: изучить методику применения критерия 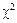Пирсона для проверки гипотезы о виде закона распределения случайной величины.

Задание: с помощью критерия 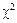проверить согласование выдвинутой гипотезы о виде закона распределения исследуемой случайной величины с имеющимися выборочными данными.

 

Алгоритм применения критерия c² для проверки гипотезы о виде
закона распределения исследуемой случайной величины.

1 Выборочные данные представляются в виде интервального или сгруппированного статистического ряда.

2 Выбирается уровень значимости a.

3 Формулируется гипотеза о виде закона распределения исследуемой случайной величины.

4 Вычисляются вероятности p_i попадания значений случайной величины Х в рассматриваемые разряды разбиения: , (), где F (x) –гипотетическая функция распределения случайной величины X.

Замечание. Если изучается непрерывная случайная величина, то при вычислении значений 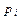необходимо изменить границы первого и последнего частичных интервалов разбиения таким образом, чтобы учесть все возможные значения, которые может принять случайная величина предполагаемого класса. В зависимости от конкретного вида проверяемой гипотезы границы частичных интервалов необходимо изменить следующим образом:

 

Вид закона распределения	Первый интервал разбиения	Последний интервал разбиения
Равномерный
Экспоненциальный
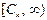
Нормальный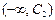

 

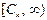
5 Определяются значения теоретических частот np_i (i = 1, 2,…, k). При необходимости для обеспечения условия np_i ³ 3 (если объем выборки 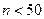), np_i ³ 5 (если объем выборки 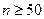), объединяются несколько соседних разрядов разбиения.

6 Вычисляется наблюдаемое значение критерия c²: .

 

7 По таблицам квантилей распределения c² определяется критическое значение 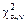, соответствующее заданному уровню значимости a и числу степеней свободы n = k – r – 1.

Если расчётное значение критерия попадает в критическую область, т. е. 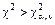, то проверяемая гипотеза отвергается (при этом вероятность отклонения верной гипотезы равна a).

В случаях, когда наблюденное значение c² не превышает критического 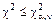, считают, что выдвинутая гипотеза не противоречит опытным данным. Подчеркнем, что полученный результат свидетельствует лишь о приемлемом согласовании проверяемой гипотезы с имеющимися выборочными данными и, в общем случае, не является доказательством истинности этой гипотезы.

 

Пример 2.1. По таблице, полученной в лабораторной работе №1 и по гистограмме частот выдвигаем нулевую гипотезу о виде закона распределения случайной величины 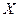(времени простоя оборудования в ожидании ремонта).

Случайная величина 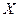(время простоя оборудования в ожидании ремонта) распределена по показательному (экспоненциальному) закону.

Выбираем уровень значимости .

Вычислим вероятности p_i попадания значений случайной величины Х в рассматриваемые разряды разбиения по формуле: = .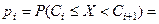

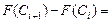
Проверим гипотезу 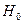с помощью критерия согласия Хи-квадрат Пирсона.

Вычислим параметр 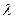= = = 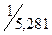0,189358 = 0,189.

Так как изучается непрерывная случайная величина, то при вычислении значений 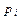необходимо изменить границы первого и последнего частичных интервалов разбиения. В нашем случае проверяется гипотеза о показательном законе распределения.

 

Вид закона распределения	Первый интервал разбиения	Последний интервал разбиения
Экспоненциальный

 

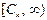
Вычислим вероятности по формуле .

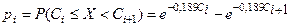Пример расчета:

1- 0,344788 = 0,655212 = 0,655.

Для того, чтобы облегчить расчеты, можно с помощью пакета программ выполнить промежуточные расчеты, которые необходимо оформить в виде таблицы:

 

Таблица 1 - Расчетная таблица вероятностей

Граница интервала
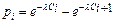
			0,655212	0,655212
5,634	-1,06483	0,344788	0,221096	0,221096
11,058	-2,08996	0,123692	0,079318	0,079318
16,482	-3,1151	0,044374	0,028455	0,028455
21,906	-4,14023	0,015919	0,010208	0,010208
27,33	-5,16537	0,005711	0,003662	0,003662
32,754	-6,19051	0,002049	0,002049	0,002049
	-		-	-
Итого	-	-

 

Таблица 2 – Расчет c²

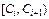
Границы интервалов	Частоты эмпирические	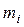Вероятности	Частоты теоретические
[0; 5,634)		0,655	26,21
[5,634; 11,058)		0,221	8,844
[11,058; 16,482)		0,079	3,173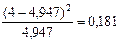
[16,482; 21,906)		0,028	1,138
[21,906; 27,33)		0,01	0,408
[27,33; 32,754)		0,004	0,146
[32,754; )		0,002	0,082
Итого				0,863 = c2

 

Вычислим число степеней свободы n = k – r – 1 = 3-1-1= 1, где k = 3– число интервалов в таблице 2 после объединения, r =1 - число параметров выбранного закона распределения – в нашем случае показательный закон (один параметр ).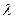

По таблицам квантилей распределения c² определяется критическое значение 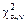= = 3,841, соответствующее заданному уровню значимости a=0,05 и числу степеней свободы n = 1.

 

Вывод. Сравниваем полученное значение в таблице 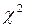= 0,863 с табличным 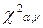= 3,841. Так как расчетное 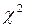= 0,863 меньше, чем табличное 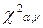= 3,841, то гипотеза о показательном законе распределения подтвердилась.

 

 

Пример.2.2

При проведении экспериментов фиксировались значения случайной величины X, характеризующей цены на зимнюю обувь (в у.е.).

Задание: произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины Х, построить гистограмму частот. По гистограмме частот выдвинуть нулевую гипотезу о виде закона распределения случайной величины 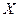и проверить ее с помощью критерия согласия Пирсона.

 

1) Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания признака) и произведем расчеты, необходимые для вычисления числовых характеристик.

 

Таблица 1- Расчетная таблица

Номер п/п	Выборка, у.е.	Вариационный ряд, у.е.,
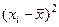
			-42,16	1777,466
			-38,16	1456,186
			-38,16	1456,186
			-30,16	909,6256
			-27,16	737,6656
			-25,16	633,0256
			-23,16	536,3856
			-23,16	536,3856
			-22,16	491,0656
			-22,16	491,0656
			-21,16	447,7456
			-18,16	329,7856
			-14,16	200,5056
			-13,16	173,1856
			-11,16	124,5456
			-9,16	83,9056
			-9,16	83,9056
			-8,16	66,5856
			-7,16	51,2656
			-6,16	37,9456
			-6,16	37,9456
			-4,16	17,3056
			-4,16	17,3056
			-1,16	1,3456
			0,84	0,7056
			0,84	0,7056
			0,84	0,7056
			4,84	23,4256
			6,84	46,7856
			6,84	46,7856
			6,84	46,7856
			6,84	46,7856
			8,84	78,1456
			9,84	96,8256
			11,84	140,1856
			12,84	164,8656
			12,84	164,8656
			13,84	191,5456
			13,84	191,5456
			15,84	250,9056
			18,84	354,9456
			22,84	521,6656
			23,84	568,3456
			24,84	617,0256
			25,84	667,7056
			26,84	720,3856
			27,84	775,0656
			30,84	951,1056
			32,84	1078,466
			55,84	3118,106
Итого				21562,72

 

2) Вычислим числовые характеристики.

Выборочное среднее: .

Мода:.

.

 

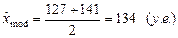Медиана: = .

В качестве оценки дисперсии используется статистика

 

= .

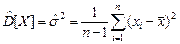Оценка среднего квадратического отклонения

 

= .

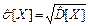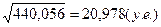Оценка коэффициента вариации

.

Найдем размах выборки = 183-85 = 98.

3) Вычислим длину интервала = = 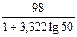14.

4) Границы интервалов:

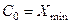= 85, = 85+14 = 99,

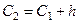= 99+14 = 113, 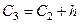= 113+14 = 127,

= 127+14= 141, = 141+14 = 155, 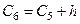= 155+ 14 = 169, = 169 +14 = 183 = .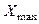

Построим гистограмму частот.

 

Рисунок 1 – Гистограмма частот

 

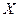Случайная величина (цены на товары (в у.е.)) распределена по нормальному закону.

Выбираем уровень значимости .

Так как изучается непрерывная случайная величина, то при вычислении значений 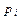необходимо изменить границы первого и последнего частичных интервалов разбиения. В нашем случае проверяется гипотеза о нормальном законе распределения.

 

Вид закона распределения	Первый интервал разбиения	Последний интервал разбиения
Нормальный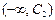

 

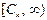
Вычислим вероятности p_i попадания значений случайной величины Х в рассматриваемые разряды разбиения по формуле: .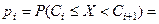

 

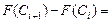
Проверим гипотезу с помощью критерия согласия Хи-квадрат Пирсона.

Вычислим параметр = 127,16, 20,978.

Вычислим вероятности по формуле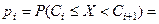

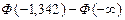= = = -0,4099+0,5 = 0,0901,

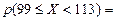
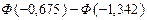= = = - 0,2517 + 0,4099 = 0,1582,

= = = - 0,0040 + 0,2517= 0,2477,

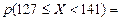
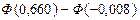= = = 0,2454 + 0,0040 = 0,2494,

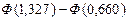= = = 0,4082- 0,2454 = 0,1628,

 

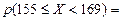
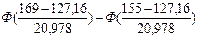= = = 0,4772- 0,4082 = 0,069,

= = = 0,5 - 0,4772 = 0,0228.

 

Таблица 2 – Расчет Хи-квадрат

Границы интервалов	Частоты эмпирические	Вероятности	Частоты теоретические
(, 99]		0,0901	4,505	0,028
(99, 113]		0,1582	7,91
(113,127 ]		0,2477	12,385	0,155
(127, 141]		0,2494	12,47	0,999
(141, 155]		0,1628	12,73	0,586
(155, 169]		0,069
(169, 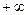)		0,0228
итого				1,768=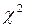

Вывод. По таблицам квантилей распределения c² определяется критическое значение 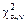= = 3,841, соответствующее заданному уровню значимости a=0,05 и числу степеней свободы .Сравниваем полученное значение 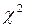= 1,768 с табличным значением 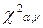= 3,841. Так как расчетное 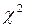= 1,768 меньше, чем табличное 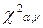= 3,841, то гипотеза о нормальном законе распределения подтвердилась.

 

 

 

Лабораторная работа № 3