% . :
d - ( int);
u - ( unsigned int);
f - ( float);
- ( float).
_ - , , () .
:
h - short int (hd);
l - long int (ld) double (lf, le);
L- long double (Lf, Le).
printf() scanf() , - . ( ), , & :
& _
:
& _
, &. name - , &name - .
, n, z, :
scanf ("%d%f%f",&n,&z,&x);
. , . n , z - float, 18 18 -0.431 n 18, z 18.0, - -0.431.
scanf() " " - , , .
16: .
/* */
#include <stdio.h>
void main()
{
double h, r, v;
const float PI = 3.14159;
/*h - , r - */
/*v - , PI - "" */
printf("\n r= ");
scanf("%lf", &r);
printf(" h= ");;
scanf("%lf, &h);
v = h * PI * r * r;
printf(" : %10.4f",v):
}
. PI, .. 3.14159 PI, .
printf(), -, . scanf() , "" (Enter), . printf() . %lf h r float, scanf() %f %. :
|
|
|
r= 2.0
h= 4.0
: 50.2654
2.0 4.0 h. :
r= 4.0
h= 2.0
: 100.5309
scanf() , &r, &h.
. , f1, f2, fi =fi-1 + fi-2 r>2. (k) , : = F1 r = F2. :
/* */
#include <stdio.h>
void main()
{
int k,i;/*- ; i- */
float s,p,r,f; /* s - */
/*: -; r - ; f- i-*/
Ml: printf("\n k=");
scanf ("%d",&k);
if(k > 2) goto M2;
printf("\n ! k > 2!");
goto Ml;
M2: printf("\n =");
scanf("%f",&p);
printf("\n r=");
scanf("%fn,&r);
i = 3;
s = p + r;
M: f = p + r;
s = s + f;
p = r;
r = f;
i = i + 1;
if (i <= k) goto M;
printf("\n : %10.3f", s);
}
, k. >2, 2. , Ml k.
, , >2.
1 .
2 (IDE ) Borland C, N:\APL\BC\BIN\BC.EXE, .
3 printf() scanf().
4 printf, scanf . , .
5 - (N:\APL\TC\LAB\*.CPP), printf (), scanf (), .
6 .
7 , , .
b=f(x,y,z), z=j(x,y). 14.
14
| . | f(x,y,z) | j(x,y) | x | y |
| e|x-y|(tg2z)x | 
| -4,52 | 0,75 | |
| 
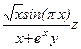
| 2,87 | 0,84 | |
| 
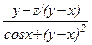
| 1,82 | 18,25 | |
| 
| 5,34 | 3,85 | |
| 
| -2,75 | -1,42 | |
| 
| 1,54 | -3,26 | |
| 
| 1,82 | 18,23 | |
| 
| -0,85 | 1,25 | |
| 
| 0,12 | -8,75 | |
| 
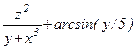
| 1,58 | 3,42 | |
| 
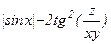
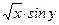
| 0,42 | -0,87 | |
| 
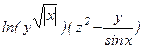
| -15,24 | 4,67 | |
| 
| 6,55 | -2,78 | |
| 
| 0,84 | 0,65 | |
| 
| 1,12 | 0,87 | |
| 
| 0,27 | 4,38 | |
| 
| 6,35 | 7,32 | |
| 
| 0,42 | 1,23 | |
| 
| 4,32 | -0,54 | |
| 
| 0,83 | 2,38 | |
| 
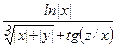
| -0,93 | -0,25 | |
| 
| 3,25 | 4,12 | |
| 
| -0,72 | -1,42 | |
| 
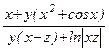
| 3,98 | -1,63 | |
| 2sin(px+y) | 3,91 | -0,51 | |
| 
| -0,62 | 5,54 | |
| 
| -4,58 | 2,32 | |
| 
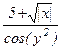
| -3,44 | 5,28 | |
| 
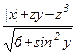
| 5,48 | 2,25 |
6
|
|
|
