Задание 1. Нарисовать блок-схему для вычисления h, взяв значения функций из таблицы 2.
Таблица 2
| Вар. | h | a | b | с | x |
| a2+b2-6c | x2-e-x | lnx+ 
| cos2x+x5 | 5,4 | |
| c2+8b+10a | sin2x+x1/4 | tgx-8x3 | x4+2sinx2 | 1,2 | |
| 3a2+4b-8 | 3x-2cos3x | lnx+2ex | x1/3+4x-1 | 0,3 | |
| a3+b2-8c | sin3x+x4 |  -lnx -lnx
| 4x-5x3 | 1,7 | |
| 6b3+4c-2 | tgx+e2x | x2-6x3 | 1/x-2lnx | 4,1 | |
| a2+b2+c2 | ex+e2x+4 | x-sin3x | x2/cos3x | 2,4 | |
| 5b3-2a+c | tgx-2x |  -sinx -sinx
| x3/7 | 5,5 | |
| 4a2+5b2 | cosx+2x | x4-2x/5 | 2x-5 | 4,6 | |
| 3ab-4c | sin2x+5 | cosx5 | x1/3+tgx | 1,6 | |
| c2+5a3-b | cos3x-6x | -4x3+lnx | e2x+4cosx | 4,6 | |
| 2a+4c-b4 | ex-2lnx | 2x-5/x | x5-2lnx | 3,9 | |
| a2+b2+c2 | 2/x+x3 | lnx2-4x | tgx-sin2x | 4,1 | |
| (a+b)2 | lnx+2ex | tgx+e2x | x2-e-x | 3,4 | |
| 2ac-3cb | 1/x-2lnx | cosx+2x | sin2x+x1/4 | 1,9 | |
| 5c+2a4 | x2-2/x | (2-x)/6 | cos3x-2x | 2,3 | |
| a+b+c | lnx/2x | x3-4x | tgx-2x | 4,2 | |
| 2a+3b+4c | x2+x3 | lnx-x4 | cos2(x-4) | 2,8 | |
| a2+b3+c4 | sin2x+x1/4 | x3+4x | ex+2lnx | 1,3 | |
| a+2b+3c | 2x-x1/4 |  -2cosx -2cosx
| tgx-4x | 3,1 | |
| 2(a+b)-c4 | (x3-x/2)3 | lnx-e2x | 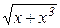
| 2,4 | |
| c2-b3 | 2x+sinx4 | sin(x-lnx) | lnx2+2x | 1,1 | |
| 3a-4cb | 2cosx3 | tgx/4 | x/5 | 3,1 | |
| c5-2ab | 1/2sin3x | sin6x/x3 | x-4sin2x | 1,8 | |
| 6a+3b3+c | cosxx+2x | sin2x+tgx | lnx-e-x | 2,1 | |
| 4abc | xx-sinx3 | x/2-x5 | 2x-sin3x | 4,1 | |
| a2+(b-c)5/3 | 2x1/3+1 | sin(x2+4) | lncos3x | 5,3 | |
| (a+4b)1/3-c2 | tg(2x)/4 | cosx2/x1/5 | e-2x+1/x2 | 3,8 | |
| a1/3+(b3-c) | x+23x | lnsin34x | arcsin2x | 4,2 | |
| b3+(a-4c)1/5 | 53x/(3x-1) | e-5x+4/x | cos(x1/3) | 2,6 | |
| c1/5-(b+3a)2 | 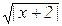 +ex +ex
| cosx+x2 | arctg(x3) | 1,3 |
Задание 2. Нарисовать блок-схему для вычисления
y = f(x), где
ì f1(z), если z < 0;
x = í f2(z), если 0 £ z £ 8;
î f3(z), если z > 8;
z = cos(с).
Значения функций приведены в таблице 3.
Таблица 3
| Вар. | f(x) | f1(z) | f2(z) | f3(z) | c |
| x2+8x-6 | z3-3z2 | zln(z) | ez-e-z | 5,1 | |
| x3lnx2 | e-z+3z | ln|z| | cosz+z2 | 5,4 | |
| x1/4+sinx | 2z-ln|z| | tgz-2z | sin3z | 4,1 | |
| x4+2sinx2 | sinz+tgz | cos3z+3/z | z2+lnz2 | 3,2 | |
| cosx3 | z2+2sinz | lnz+2z | ez+1/z | 4,7 | |
| sinx+2lnx | 2z+tgz | lnz4+2z | cosz+2z | 1,3 | |
| sin4x2 | sinz2-z3 | 
| 2sinz2 | 1,6 | |
| tgx-4x3 | 1/cos2z | z-ln|z| | z3+sinz | 1,5 | |
| lnx-e2x | z2+ez | cos4z/z3 | tg(z+1/z) | 2,7 | |
| 2x-lnx | 2cosz+1/z | z3-2ln|z| | tg2z+z3 | 3,8 | |
| 3x-sinx | 3tg3z | 1/cos4z | e2z+sinz | 1,6 | |
| 4x2+cosx | 3z/sinz | z2+2sinz | 2z-ln|z| | 2,4 | |
 +cosx +cosx
| z2+lnz2 | ez+1/z | z4-sinz | 4,1 | |
| x1/3+2x | ln|cosz| | 2z+ez | tg2z | 2,5 | |
| sin4x+2x | z5/sin2z | e-2z+tgz | cos4z+z1/3 | 3,2 | |
| tg4x+1/x | z/sinz1/5 | 2ztg3z | z  +8 +8
| 1,4 | |
| ln(1/x) | zsin2z-8 | lnsinz0,8 | 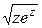 -2,5 -2,5
| 2,3 | |
| e2x+4x | cos(p /4)-z | 1/(ez+1) | arctg(z+3) | 4,1 | |
| cosx4+x/2 | sin(z+30°) | lncos(pz/6) | e-tg(z-2) | 3,2 | |
| 2tgx+ex | z+cos(p +z) | z3+z1/3 | z4-lnz | 2,8 | |
| 2lnx2 | arccosz2 | sinz+lncosz | z3-sin(p x) | 1,7 | |
| cos2x/3 | z2+ln(z+4) | e(z-5)+sinz | 
| 2,2 | |
| 1/tgx4 | e-4z+2+z2 | cos(z1/3+2) | sin(p +4z2) | 5,6 | |
| e2x-x3 | tg(z2+  ) )
| ln(sinz+5) | z4+z2-cosz | 3,4 | |
| tgx-2lnx | arcsin(z+3) | z3-z2+cosz | ln(z3+4z) | 2,5 | |
| cosx4+x/2 | lnsinz0,8 | cos(p /4)-z | z/sinz1/5 | 3,7 | |
| ln(x+x2) | 2ztg3z | sin(p +4z2) | z3+z1/3 | 2,6 | |
| cosx4+2x | tg(z+1/z) | e2z+sinz | cosz1/5 | 3,8 | |
| sin4x+2x | z2+lnz2 | cos3z+3/z | cos(p /4)-z | 5,8 | |
| 3ln(x2+5) | z4-lnz | sinz+tgz | sinz+lncosz | 3,5 |
Задание 3. Найти сумму ряда
y =  , где a £ x £ b, D x = c.
, где a £ x £ b, D x = c.
Варианты заданий приведены в таблице 4.
Таблица 4
| Вар. | f1 | f2 | a | b | c |
| 3x-1 | e-1/x+x/(x+1) | 0,5 | |||
| x3-3x2 | x4+2x2+3 | 0,2 | |||
| e-x+4x | 
| 0,6 | 4,2 | 0,3 | |
| sin2(x+4x3) | (x+2x3) 
| 0,5 | 4,8 | 0,2 | |
| xsinx3-ln2x | arctgx/4+e-x+2 | 6,3 | 0,4 | ||
| x4-cosx | tgx+2x | 0,5 | |||
| 2x+sin2x | 
| 0,3 | |||
| ln(4x+8) | e-x+sin2x | 0,2 | |||
| x3ln(2x) | 4x2+6x3-2 | 0,5 | 0,3 | ||
| x2+sin3x | cos3x+e-2x | -2 | 0,4 | ||
| xe-x | sin4x+x3 | 1,5 | 0,3 | ||

| arctgx/5+2x | 0,6 | 0,2 | ||
| x2/(3x+2) | sin2(p x+1) | 0,5 | 5,2 | 0,3 | |

| 3x/(x-2) | 1,2 | 6,3 | 0,4 | |
| x3x+1+8x | |x-8|+sinx | 7,5 | 0,3 | ||
| x4+ex+3 | xarctg(x/3) | 6,4 | 0,2 | ||
| ln2(x+4) | sin3(x/5) | 6,8 | 0,3 | ||
| ex-2+x3 | x-ln|x-1| | 0,4 | |||
| 2cos(x+3) | 4x2/(3+x3) | 0,3 | |||
 ) )
| tg2(x+4)-e-x | 0,4 | |||
| 3+2sin2(x-3) | 4+x/10 | 0,5 | |||
| ln(1(1+2x) | sin2(4x+1) | 1,5 | 6,8 | 0,4 | |
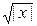 +e-x +e-x
| 5arctg(4x) | 0,5 | |||
| arcsin(x+2) | 3(x-4)/(x2+1) | 0,2 | |||
| e|x+2| | ln2(x+4) | -2 | 0,3 | ||
| (4-x)cos2x |  +e-3x +e-3x
| 0,4 | |||

| sinx4-4 | -2 | 0,2 | ||
| 2x+4+cos2x | ln|x+8| | -4 | 0,5 | ||
| (x+2)/sin3x | 
| 0,3 | |||
| ex+3+4x2 | arcsinx3 | 0,2 |
Лабораторная работа 2
СЕЛЕКТИВНАЯ ОБРАБОТКА МАССИВОВ
Цель работы: выработать практические навыки в составлении алгоритмов, написании и отладке программ в задачах селекции в одномерном массиве.
Общие сведения
1 Селективная (выборочная) обработка информации
Селективная обработка заключается в обработке только той информации, которая удовлетворяет заданному условию.
Пример 5. Подсчитать количество положительных чисел в массиве x(10).
Порядок работы
Шаг 1. Вводим массив x(10).
Шаг 2. Задаем начальное значение количества k = 0.
Шаг 3. Организовываем цикл, перебирающий элементы массива (т.е. индекс i), начиная с 1-го и кончая 10-м.
Шаг 4. Если xi > 0, тогда присваиваем k = k + 1.
Шаг 5. Если цикл по i не закончился, идем на начало цикла, т.е. на шаг 3.
Шаг 6. Печатаем k.
Шаг 7. Останов.
2 Нахождение экстремального значения
Пример 6. Найти минимальное число из интервала [5,12] в массиве x(15).
Порядок работы
Шаг 1. Вводим массив x(15).
Шаг 2. Задаем начальное значение минимального элемента xmin=10 20.
Шаг 3. Организовываем цикл, перебирающий элементы массива (т.е. индекс i), начиная с 1-го и кончая 15-м.
Шаг 4. Если xi не принадлежит интервалу [5,12], тогда идем на шаг 6.
Шаг 5. Если xi < xmin, тогда присваиваем xmin = xi.
Шаг 6. Если цикл по i не закончился, идем на начало цикла, т.е. на шаг 3.
Шаг 7. Печатаем xmin.
Шаг 8. Останов.
Пример 7. Найти максимальное число и его номер в массиве x(30).
Порядок работы
Шаг 1. Вводим массив x(30).
Шаг 2. Задаем начальные значения максимального элемента и его номера: xmax = x1, nmax = 1.
Шаг 3. Организовываем цикл, перебирающий элементы массива (т.е. индекс i), начиная со 2-го и кончая 30-м.
Шаг 4. Если xi>xmax, тогда присваиваем: xmax=xi, nmax=i.
Шаг 5. Если цикл по i не закончился, идем на начало цикла, т.е. на шаг 3.
Шаг 6. Печатаем xmax, nmax.
Шаг 7. Останов.

|
Блок-схема
3 Формирование одномерного рабочего массива
В рабочий массив из исходного выбираются только те элементы, которые удовлетворяют поставленному условию.
Пример 8 Сформировать новый массив из положительных чисел исходного массива x(15).
Порядок работы
Шаг 1. Вводим массив x(15).
Шаг 2. Устанавливаем начальный индекс рабочего массива j=0.
Шаг 3. Организовываем цикл, перебирающий элементы исходного массива (т.е. индекс i), начиная с 1-го и кончая 15-м.
Шаг 4. Если xi £ 0, то идем на шаг 7.
Шаг 5. Устанавливаем индекс следующего элемента рабочего массива j = j + 1.
Шаг 6. Присваиваем элементу рабочего массива значение элемента исходного массива yj = xi.
Шаг 7. Если цикл по i не закончился, идем на начало цикла, т.е. на шаг 3.
Шаг 8. Печатаем j элементов рабочего массива y.
Шаг 9. Останов.
3.7 Сортировка элементов массива
Сортировка - это упорядочение множества по убыванию или возрастанию признака, общего для всех элементов множества. Сортировку удобно производить методом выталкивания. Если надо отсортировать часть массива, удовлетворяющую заданным условиям, то вначале отбирают нужные элементы в рабочий массив, а затем его сортируют. Если рабочий массив не сформировался, то выводят об этом сообщение и останавливают программу.
Пример 9. Найти сумму двух наибольших отрицательных чисел массива x(15).
Порядок работы
Шаг 1. Вводим массив x(15).
Шаг 2. Устанавливаем начальный индекс рабочего массива j=0.
Шаг 3. Организовываем цикл, перебирающий элементы исходного массива (т.е. индекс i), начиная с 1-го и кончая 15-м.
Шаг 4. Если xi ³ 0, то идем на шаг 7.
Шаг 5. Устанавливаем индекс следующего элемента рабочего массива j = j + 1.
Шаг 6. Присваиваем элементу рабочего массива значение элемента исходного массива yj = xi.
Шаг 7. Если цикл по i не закончился, идем на начало цикла, т.е. на шаг 3.
Шаг 8. Если j < 2, то выдаем сообщение «Массив не сформирован» и идем на шаг 17.
Шаг 9. Организовываем цикл, определяющий количество просмотров рабочего массива (т.е. индекс k), начиная с 1-го и кончая j -м.
Шаг 10. Организовываем цикл, определяющий просматриваемую пару чисел рабочего массива (т.е. индекс i), начиная с 1-го и кончая (j-1) -м.
Шаг 11. Если первое число не больше второго, то идем на шаг 13.
Шаг 12. Меняем два числа местами:
c = yi; yi = yi+1; yi+1 = c.
Шаг 13. Если цикл по i не закончился, идем на начало цикла, т.е. на шаг 10.
Шаг 14. Если цикл по k не закончился, идем на начало цикла, т.е. на шаг 9.
Шаг 15. Вычисляем сумму s = yj + yj-1.
Шаг 16. Печатаем s.
Шаг 17. Останов.






