Автокорреляция имеет место, если нарушено третье условие Гаусса-Маркова.
Последствия автокорреляциив некоторой степени сходны с последствиями гетероскедастичности, перечислим их:
1) оценки коэффициентов регрессии будут неэффективны;
2) стандартные ошибки коэффициентов будут оценены неправильно, чаше всего занижены, иногда настолько, что нет возможности воспользоваться для проверки гипотез соответствующими точечными критериями;
3) прогнозы по модели получаются неэффективными.
Для выявления наличия автокорреляции наиболее часто используют ряд критериев:
1) Графический метод;
2) Тест Дарбина-Уотсона
3) Тест серий (Бреуша-Годфри)
4) Q-тест Льюинга-Бокса
Графический метод выявления автокорреляции
Для реализации этого метода в окне результатов оценки динамической модели Multiple Regression Results выберем вкладку Residuals / assumptions / prediction, нажмем кнопку Perform residual analysis, деле в окне Residual Analysis выберем вкладку Residuals (Остатки) и кнопку Residuals vs. independent var.
В окне Select variable for scatter plot укажем переменную t1, получаем следующий график:
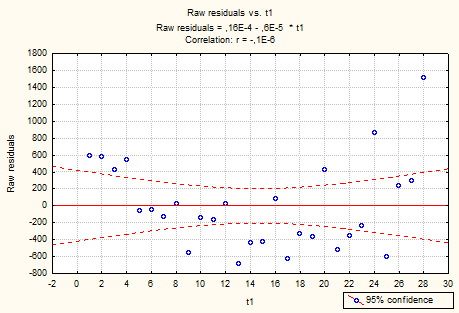
Рисунок 5.9 – Динамики случайного члена временного ряда
Согласно данным, представленным на рисунке 5.10, не прослеживается тренда в отклонениях, соответственно можно предположить отсутствие автокорреляции.
Тест Дарбина-Уотсона
Для реализации теста Дарбина-Уотсона в пакете STATISTICA в окне результатов Residual Analysis выбрать вкладку Advanced (Расширенные) и нажать кнопку Durbin-Watson statistic (Критерий Дарбина-Уотсона).
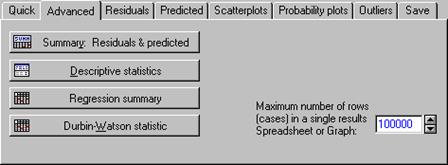
Рисунок 5.10 – Выбор критерия Дарбина-Уотсона (приведена часть исходного окна)
В результате оценки получаем следующую таблицу 5.7:
Таблица 5.7 – Значение критерия Дарбина-Уотсона
| Durbin- Watson | Serial Corr. | |
| Estimate | 1,317 | 0,230 |
Значение критерия отлично от двух (приложение _____), при этом согласно таблице критических значений данной статистки при n =25 и k =2 нижняя граница dн =1,21 и верхняя граница dв =1,55. Отсюда получаем, что фактическое значение попадает в зону неопределенности dн < DW < dв, соответственно невозможно точно сделать вывод о наличии (отсутствии) автокорреляции (см. рисунок 5.11).
| Есть положительная автокорреляция остатков. Н0 отклоняется с вероятностью Р =(1-a) принимается Н1 | Зона неопределенности | Нет оснований отклонять Н0 (автокорреляция остатков отсутствует) | Зона неопределенности | Есть отрицательная автокорреляция остатков. Н0 отклоняется с вероятностью Р =(1-a) принимается Н1 |
| 0 dн dв 2 4- dн 4- dв 4 |
Рисунок 5.11 - Механизм проверки гипотезы о наличии автокорреляции остатков
Тест серий Бреуша-Годфри
Для реализации данного теста в пакете STATISTICA 6.0, необходимо выполнить следующие шаги:
Шаг 1. Воспользуемся результатами оценки тренда -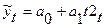 
, найдем значения случайного члена et. Для этого в окне Residual Analysis выберем вкладку Save и нажмем единственную доступную кнопку Save residuals & predicted, при этом появится окно Select variables to save with predicted/residual scor… не выбирая переменных сразу нажмем кнопку ОК. (см. глава 4).
Шаг 2. В связи с тем, что для реализации теста необходимо оценить уравнение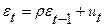 
образуем новую переменную et-1 . Для этого в главном меню выберем Insert ® Add Variables … в появившемся окне Add Variables в поле Name: (имя) внесем название переменной – Residuals t-1.
В результате образования новой переменной получаем таблицу представленную на рисунке 5.12.
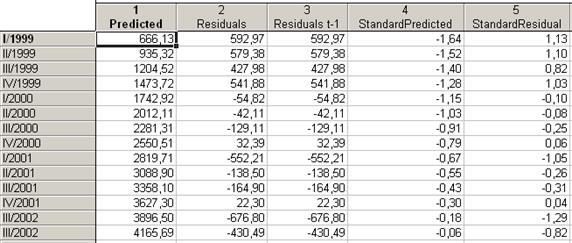
Рисунок 5.12 – Исходная таблица для построения уравнения вида - 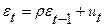(приведена часть исходного окна)
Шаг 3. Далее произведем сдвиг на один уровень вперед, для этого выберем Date ® Shift (Lag) (Данные ® Выделить лаг). В появившемся окне Shift Variables (рисунок 5.13) в поле Lag укажем значение 1.
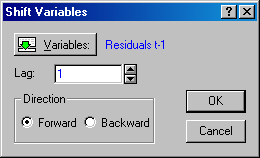
Рисунок 5.13 – Создание запаздывающей переменной
Шаг 4. На данном шаге запустим модуль Multiple Regressions и в качестве зависимой переменной укажем Residuals а в качестве независимой переменной Residuals t-1.
Шаг 5. Выставим галочку возле опции Advanced options (stepwise or ridge regressions) в появившемся окне Model Definition в прокрутке Intercept выберем Set to zero (т.е. регрессионное уравнение будет оценено без свободного члена). После оценки получим следующие результаты:
Таблица 5.8 – Результаты оценки модели вида -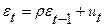
| Beta | Std.Err. of Beta | B | Std.Err. of B | t(26) | p-level | |
| Residuals t-1 | 0,194 | 0,192 | 0,230 | 0,228 | 1,009 | 0,322 |
Согласно результатам построения модели 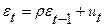, представленным в таблице 5.8, параметр r получен статистически не значим, т.е. можно утверждать об отсутствии корреляция между соседними наблюдениями на лаге 1.
