В пакете STATISTICA 6.0 существует возможность расчета огромного числа дескриптивных (описательных, элементарных) статистик (максимальные, минимальные, средние, показатели распределения и эксцесса и т.д.).
Прежде чем приступить к выполнению данного пункта, необходимо внести данные содержащиеся в приложении Е в рабочую таблицу пакета и сохранить их на жестом диске (см. лабораторная работа 1).
Для расчета описательных статистик необходимо:
Шаг 1. В главном меню выбирать Statistics ® Basic Statistics/Tables (Вычисления ®Основные статистики и таблицы).
Шаг 2. В окне Basic Statistics and Tables выбирать первый пункт Descriptive statistics (Описательные статистики).
Шаг 3. В окне Descriptive statistics выбирать вкладку Advanced (Расширенные). Данное окно разделено на три группы показателей (рисунок 3.1):
1) Location, valid N (Объем совокупности) – содержатся структурные и степенные средние величины: Valid N (Число наблюдений N), Mean (Средняя), Sum (Сумма), Median (Медиана), Mode (Мода), Geom. Mean (Геометрическая средняя), Harm. Mean (Гармоническая средняя).
2) Variation, moments (Вариация, момент) – содержатся показатели относящиеся к вариации изучаемого признака и отражающие распределение переменной: Standard Deviation (Стандартное Отклонение), Variance (Вариация), Std. err. of mean (Стандартная ошибка среднего), Conf. limits for means (Доверительная граница для среднего), Skewness (Ассиметрия), Std. err., Skewness (Стандартная ошибка Ассиметрии), Kurtosis (Эксцесс), Std. err., Kurtosis (Стандартная ошибка Эксцесса);
3) Percentiles, ranges (Персентели, ранги) – в группе собраны следующие показатели Minimum & Maximum (Максимум и минимум), Lower & upper quartiles (Нижний и верхний квартили), Percentile boundaries (), Range (Ранг), Quartile range (Ранг квартиля).
Шаг 4. Выберем для анализа следующие показатели (рисунок 3.1): Valid N (Число наблюдений N), Mean (Средняя арифметическая), Standard Deviation (Стандартное Отклонение), Skewness (Ассиметрия), Kurtosis (Эксцесс), Minimum & Maximum (Максимум и минимум).
После нажатия кнопки Summary (Вычислить) получаем следующие результаты:
Таблица 3.1 - Описательная статистика
| Valid N | Mean | Minimum | Maximum | Std.Dev. | Skewness | Kurtosis | |
| Y | 37,667 | 11,684 | 0,266 | -1,588 | |||
| X1 | 32,400 | 13,809 | 0,225 | 0,675 | |||
| X2 | 47,533 | 6,621 | -0,442 | -1,125 |
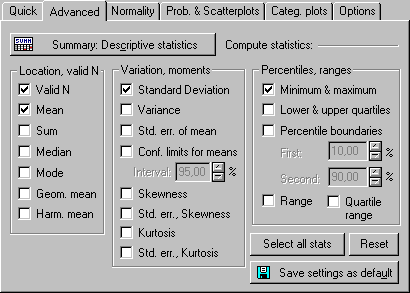
Рисунок 3.1 – Окно выбора (установок) описательных статистик (приведена часть исходного окна)
Для симметричного распределения, в частности для нормального распределения, асимметрия (Skewness) равна нулю. Если асимметрия больше трех, то распределение имеет более «длинный правый хвост». Если асимметрия меньше трех, то распределение имеет более «длинный левый хвост».
В нашем примере для всех переменных значение асимметрии близко к нулю. Это указывает на то, что распределения переменных Y, Х1 и Х2 близки к симметричным.
Если эксцесс (Kurtosis) больше нуля, то распределение островершинное относительно нормального. Если эксцесс меньше нуля, то распределение «туповершинное» относительно нормального. В нашем случае распределение переменных Y и Х2 туповершинное, а переменной X1 – островершинное.
Более точный ответ о нормальности распределения можно получить, если обратится к вкладке Normality (Нормальность) в окне Descriptive statistics (рисунок 3.2).
В пакете программ для выявления нормальности распределения исследуемых показателей используются следующие критерии:
Kolmogorov-Smirnov & Lillifors test for normality – (Критерий Колмогорова-Смирного и Критерий Лиллиефорса ) согласно этому критерию, если вычисленная D -статистика значима, то гипотеза о том, что данные имеют нормальный закон распределения, должна быть отвергнута. Иначе, гипотеза о нормальном распределении не отвергается
Shapiro-Wilk’s W test – (W Критерий Шапиро-Уилкса) согласно этому критерию, если рассчитанная по данным наблюдений W -статистика значима, то гипотеза о том, что данные имеют нормальный закон распределения, должна быть отвергнута.
Таким образом, если вероятность отклонения гипотезы о значимости D -статистики имеет значения большие выбранного уровня значимости a (обычно a = 0,01, 0,05 или 0,1), то гипотеза о нормальном законе распределения данных принимается с вероятностью (1 - a).
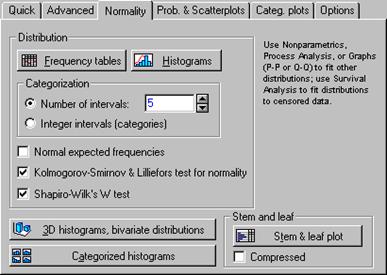
Рисунок 3.2 – Окно установок вычисления характеристики нормальности распределения (приведена часть исходного окна)
Для расчета перечисленных статистик установим, галочки как показано на рисунке 3.2, и выберем кнопку Frequency tables (Таблицы частот). В рабочей книге (Workbook) будут выведены три таблицы (в соответствии с количеством анализируемых переменных), рассмотрим результаты расчета по переменной Y.
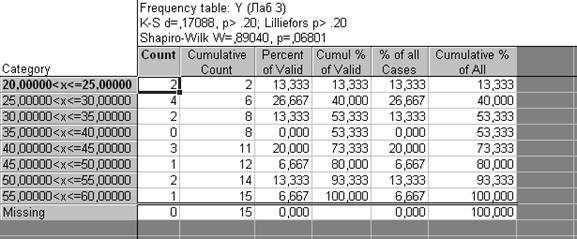
Рисунок 3.3 – Результаты оценки критериев нормальности распределения переменных (приведена часть исходно окна)
В верхней части окна приведены значения показателей, в данном случае и критерий Колмогороса-Смернова и Шапиро-Уилкса получены незначимыми и соответственно нельзя считать распределение переменной Y нормальным.






