Лабораторная работа 3 - Построение классической линейной регрессии
Цели и задачи лабораторной работы
В данной лабораторной работе на практическом примере рассмотрим этапы построения уравнения классической линейной регрессии, при этом будут решаться следующие задачи:
1) Рассчитать описательные статистики, характеризующие изучаемые данные;
2) Определить парные коэффициенты корреляции и на их основе выявить факторы, оказывающие наибольшее влияние на результативный показатель;
3) Оценить регрессионное уравнение имеющимися факторами. Проанализировать множественные коэффициенты корреляции и детерминации, по полученной модели;
4) Оценить качество модели на основе t -статистики Стьюдента и F -статистики Фишера.
Понятие классической линейной регрессии
В данной глава остановимся на рассмотрении понятия классической линейной регрессии, при этом рассматриваются два возможных случая:
Множественная регрессия представляет собой модель результативного признака с двумя и большим числом факторов, т. е. модель вида:
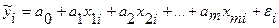
| (3.1) |
Парная линейная регрессия представляет собой частный случай множественной регрессии и есть модель между двумя переменными - у и х, т.е. имеем:
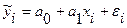
| (3.2) |
где: i =1, 2, …, n
n – объем изучаемой совокупности;
- данные полученные в результате построения модели (теоретические уровни, модельные данные)
y – зависимая переменная;
x – независимая переменная;
a0, a1 – искомые параметры уравнения;
εi – случайная величина (возмущение, остатки, отклонения).
Основным методом решения задачи нахождения параметров а 0 и а 1 уравнения связи является метод наименьших квадратов (МНК). Он состоит в минимизации суммы квадратов отклонений фактических значений от значений, вычисленных по уравнению связи.
Основным параметром парного уравнения регрессии является параметр а1 (в случая множественной регрессии аj где j = 1, 2, …, m) которыйхарактеризует силу связи между вариацией факторного признака x и вариацией результативного признака y;
Иногда в эконометрических исследованиях возникают ситуации, в которых использование параметров аj не дает желаемого результата, так как коэффициент имеет размерность совпадающую с анализируемым показателем и не пригоден для выявления наибольшего (наименьшего) влияния той или иной независимой переменной. В этом случае используют b - коэффициент или коэффициент эластичности.
b - коэффициент (стандартизованный коэффициент регрессии) показывает, на сколько среднеквадратических отклонений (b) изменится результативный признак, если величина факторного признака изменяются на одно среднеквадратическое отклонение.
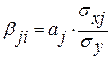
| (3.3) |
Коэффициенты условно-чистой регрессии полезно выразить в виде относительных сравниваемых показателей связи, коэффициентов эластичности:
| (3.4) |
Значение коэффициента определяет, на сколько процентов в среднем изменится значение зависимой переменной y если независимая переменная x изменится на 1%.
В большинстве случаев при построении модели приходится пользоваться выборочными данными, поэтому прежде чем приступать к использованию модели необходимо убедится ее адекватности фактическим данным (анализируемому явлению). Для этих целей используют t-критерий Стьюдента и F-критерий Фишера.
Рекомендуемая литература
Для лучшего понимания материала изложенного в данной главе необходимо дополнительно проанализировать следующие источники литературы (см. список использованных источников):
| Номер в списке литературы | Страницы | Номер в списке литературы | Страницы |
| 2.1 | 30-61, 77-91 | 2.10 | 49-53 |
| 2.5 | 53-73, 134-159 | 2.12 | 43-155 |
| 2.7 | 50-108 | 4.6 | 160-174, 179-215 |
| 2.8 | 27-50, 60-71 | 4.10 | 96-122 |
