Рассмотрим последовательность 
, где 
. Найдем несколько членов этой последовательности:
; 
; 
; …,
; 
; 
.
Как можно заметить, члены последовательности возрастают с увеличением их номеров.
Если последовательность монотонно возрастает 
" n и ограничена, то по теореме Вейерштрасса она имеет предел. Покажем, что рассматриваемая последовательность удовлетворяет этим требованиям.
Покажем сначала, что рассматриваемая последовательность монотонно возрастает, т. е. 
" n.
Воспользуемся формулой разложения бинома Ньютона, которая имеет вид
.
Запишем разложение члена последовательности 
по этой формуле
.
Здесь в слагаемых каждый сомножитель, стоящий в числителе дробей, поделим на n, имеющееся в знаменателе. Получим
.
Также поступим с 
.
.
Так как слагаемые в разложении меньше соответствующих слагаемых в разложении :
, 
, …, 
" k Î N,
то 
.
Покажем, что последовательность ограничена. Запишем
.
Поделим каждую скобку в числителе на n, получим
.
Каждая скобка в правой части этого равенства меньше единицы, поэтому справедливо неравенство
.
Усилим данное неравенство. Уменьшим знаменатели дробей, заменив факториалы, стоящие в знаменателях на степени:
; 
; 
, …, 
,…, 
.
Имеем неравенство 
, правая часть которого при n ®¥ представляет бесконечную убывающую геометрическую прогрессию. Найдем сумму этой бесконечной прогрессии, получим
.
Следовательно, последовательность ограничена.
Таким образом, последовательность с общим членом имеет предел. Этот предел равен
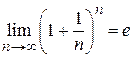, (1.2)
где e = 2,718281828… - иррациональное число.
Покажем, что второй замечательный предел может быть записан в следующем виде
, где 
- непрерывная бесконечно малая функция.
Значение любой бесконечно малой функции a(х) при конкретном значении х удовлетворяет неравенству
,
где n подходящее достаточно большое число.
Отсюда можно записать два неравенства
и 
.
Тогда справедливо неравенство
.
При этом если a(х)®0, то n ® ¥.
Так как
,
,
т. е. 
, то по теореме 1.8 о промежуточной функции
. (1.3)
Данное число е, являясь основанием экспоненциальной функции 
, имеет большое значение в математике и естественных науках.
Второй замечательный предел может быть использован при раскрытии неопределенностей типа 
, но не любого вида, а только в том случае, когда добавка к единице a(х) и степень находятся в строго определенном соотношении. К единице должна прибавляться бесконечно малая функция (величина), а степень должна являться обратной к этой функции (величине).
Пример 1.8. Найти предел 
.
Р е ш е н и е. Так как в основании функции под пределом к единице добавляется 
, то для того, чтобы применить второй замечательный предел, степень должна быть равна обратной к ней величине, т. е. 
. Именно эту степень записываем, а затем с помощью алгебраических действий преобразуем ее к первоначальному виду, т. е. к n.
.
Учитывая то, что степени перемножаются при возведении в степень, получаем 
.
Пример 1.9. Найти предел 
.
Р е ш е н и е. Прежде всего необходимо убедиться, что в данном пределе имеется возможность применить второй замечательный предел. Для этого и найдем предел 
. Следовательно, имеет место неопределенность типа .
Затем отдельно ищем предел числителя и знаменателя
.
С пределами в числителе и знаменателе поступаем так же, как в предыдущем примере 1.8, т. е. вместо степени х записываем степени, которые требуется для применения второго замечательного предела, а затем их компенсируем.
Получаем
.
При нахождении этого предела возможен другой способ решения, введение новой переменной. Обозначим основание функции под пределом через 1+a, получим 
Þ 
Þ 
.
Определяем, к чему стремится a: 
.
Находим предел
.
