1) Δy ≈ y’ Δx = dy – дифференциал функции.
y(x0 + Δx) – y(x0) = y’Δx
y(x0 + 
x) = y(x0) = y(x0) + y’(x0) 
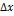(1)
По формуле (1), зная значение 
, y(x0), y’(x0) можно определить y(x0 + Δx).
2) Рассмотрим функцию 
. Дифференциал этой функции 
зависит от 
и 
, причем 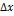не зависит от , так как приращение в данной точке можно выбирать независимо от . В этом случае 
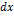в формуле первого дифференциала будет постоянным. Тогда выражение 
зависит только от и его можно дифференцировать по .
Дифференциал от дифференциала функции 
в данной точке называется дифференциалом второго порядка или вторым дифференциалом.
Аналогично: 
.
Найдем формулу для вычисления второго дифференциала
т.е. 
Аналогично получаем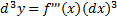 
Можно установить справедливость формулы
r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
Отсюда получаем 
В частности, при n=1,2,3...
При этом предполагалось. что 
- независимая переменная.
Пусть теперь 
. Тогда 
.
Поэтому при вычислении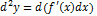 
будем считать его как дифференциал от произведения двух функций
Итак, 
Для дифференциала третьего порядка имеет место формула 
Из полученных формул следует, что при вычислении дифференциалов более высоких порядков от сложной функции происходит нарушение инвариантности формы.
Билет №23
Теорема Ролля, ее геометрический смысл
Теорема: если функция y=f(x) непрерывна на отрезке [a,b], и 1. Имеет конечную производную f’(x), x ϵ (a,b), 2. f(a) = f(b), тогда Ǝ точка с ϵ (a,b) такая что f’(c) = 0.
Доказательство: По 2-ой теореме Вейерштрасса f(x) достигает наибольшего значения на [a,b]. Пусть М – наибольшее значение f(x), m – наименьшее значение f(x) на [a,b].
1. M=m так как f(a)=f(b) f(x)=f(a)=f(b)=const и условие f’(x) = 0 выполняется для любых хϵ(a,b).
2. M≠m f(x) не может принимать наибольшего(наименьшего) значения при x=a(x=b) то есть Ǝ точка cϵ(a,b) для которой f(x) =max(min) по т.Ферма в этой точке f’(c) =0.
Из теоремы Ролля следует, что существует точка х=с, на отрезке [a,b], в которой касательная к графику функции f(x) параллельна оси ox.
Билет №24
Теорема Лагранжа о конечном приращении функции, ее геометрический смысл
Пусть функция f(x):
1. Непрерывна на отрезка [a,b]
2. Дифференцируема в интервале (a,b)
Тогда существует точка x=c на отрезке [a,b] такая, что f(b) – f(a) = f '(c)(b-a)
Существует точка x=c на отрезке (a,b), в которой касательная к графику функции f(x) параллельная прямой, проходящей через хорду графика или совпадающая с ней.
Доказательство: Рассмотрим вспомогательную функцию F(x) =f(x) – f(a) - 
(x-a) (1)
Функция (1) удовлетворяет всем условиям т.Ролля F(b)=F(a) F(b)=0, F(a)=0.
Это значит, что существует т сϵ(a,b), для которой F’(c) = 0.
F’(x) = f(x) -
F’(c) = f’(c) – 
=> f’(c) =
Билет №25
