Билет №1
Множества, способы их задания. Операции над множествами (объединение, пересечение).
Под множеством понимают совокупность некоторых объектов, объединенных по какому-либо признаку.
Множества могут быть конечными, бесконечными и пустыми.
Множества могут быть заданы списком, порождающей процедурой, арифметическими операциями, описанием свойств элементов или графическим представлением.
1. Задание множеств списком предполагает перечисление элементов. Например, множество 
состоит из букв 
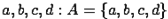или множество 
включает цифры 
.
2. Задание множеств порождающей процедурой или арифметическими операциями означает описание характеристических свойств элементов множества: 
, т. е. множество 
содержит такие элементы 
, которые обладают свойством 
.
o 
, 
- множество всех натуральных чисел;
o 
3. Задание множества описанием свойств элементов: например,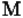 
- это множество чисел, являющихся степенями двойки.
4. Графическое задание множеств происходит с помощью диаграмм Эйлера-Венна. Замкнутая линия-круг Эйлера - ограничивает множество, а рамка - универсальное пространство 
. Заданы два множества: 
и 
. Если элементов множеств немного, то они могут на диаграмме указываться явно.
Объединением множеств и 
(
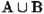) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств или . Даны два множества: 
и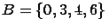 
. Найдем множество 
.
Пересечением множеств и (
) называется множество, состоящее из элементов, входящих как в множество , так и в множество : 
. Даны множества и 
. Найдем их пересечение: 
.
Билет №2
Функции, способы их задания, классификация.
Пусть даны 2 непустых множества A={x ∣x ∈ A}, B={y ∣y ∈ B} пусть f - некоторое отношение между А и В, если пара (х, у) является элементом отношения f, то говорят, что элементу у соответствует элемент х или элементу х сопоставляется элемент у.
Отношение f между А и В, при котором каждому элементу из А соответствует не более одного элемента из В называется функцией.
Различают 4 способа задания функции:
| х | х1 | х2 | х3 | х4 |
| у | у1 | у2 | у3 | у4 |
1. Табличный. Указывается значение аргумента x и соответствующе значение функции y=f(x).
2. Аналитический. Является наиболее важным для МА (мат. анализа), поскольку методы МА (дифференциального, интегрального счисления) предполагают этот способ задания. Одна и та же функция может быть задана различными формулами: y=∣sin(x)∣y=√1−cos2(x).
3. Графический. Область определения -- проекция данного графика на Ох, а множество значений -- проекция Д(f) на Оу.
4. Словестный. Например, y=[x]: x из R (Целой частью х из R называют любое целое число не превосходящее х).
Имеет место следующая классификация функций:
1) Функция вида Pn (x)=a0xn + a1xn-1 + a2xn-2 + … + an, где n ∊ N∪{0}, a0, a1, …, an ∊ R, называется целой рациональной функцией или многочленом степени n.
2) Функция, представляющая собой отношение двух целых рациональных функций
называется дробно иррациональной. Совокупность дробно иррациональных и целых рациональных называется рациональными функциями.
3) Функция, полученная с помощью конечного числа суперпозиций и четырех арифметических действий над степенными функциями как с целыми так и с дробными показателями и не являющиеся рациональными называются иррациональными.
y=√x, f(x)= 
Рациональные и иррациональные функции образуют класс алгебраических функций.
4) Всякая функция, не являющаяся алгебраической, называется трансцендентной.
Элементарные функции
Алгебраические ф-ции Трансцендентные ф-ции
Рациональные ф-ции Иррациональные ф-ции
Целые ф-ции Дробные рац-ные ф-ции
Билет №3
Окрестность точки, предельная точка множества. Понятие стремления дискретной непрерывной величины к предельной точке. Определение предела функции непрерывного аргумента по Коши при х → х0 и х →∞.
На числовой оси окрестность точки – любой интервал (открытый промежуток), содержащий данную точку. В частности открытый (не содержащий границ) промежуток (а – δ; а + δ) с центром в точке а называется δ -окрестностью точки а (положительное число δ – радиус δ -окрестности).
В n-мерном пространстве окрестность точки – любая область, содержащая данную точку.
Окрестность точки А в метрическом пространстве – любая область, содержащая точку А. В частности все точки М, расстояние от которых до точки А меньше некоторого положительного числа δ, образуют ее (т.е. точки А) сферическую окрестность радиуса δ с центром в точке А.
Точка Р называется предельной точкой множества М, если в любой окрестности точки Р имеется, по крайней мере, ещё одна точка множества М, кроме точки Р.
Оказывается, в любой окрестности предельной точки содержится бесконечное число точек множества М. Сама же предельная точка может как принадлежать, так и не принадлежать множеству М.
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
Билет №4
